Збірник завдань для олімпіад "Задачі на побудову"

ЗАДАЧІ НА ПОБУДОВУ

8 клас

(ЧАСТИНА 3)

 ЗМІСТ

Вступ                                                                                                                        

Частина І.  Задачі на побудову за допомогою циркуля й лінійки. 

1.          Поняття задачі на побудову.
2.          Схема розв'язування задач на побудову.

Частина ІІ.  Загальні методи розв’язування задач на побудову:

1.  Метод геометричного місця точок.

2. Метод перетворення площини (симетрія, паралельне перенесення, поворот, гомотетія).

          3. Чудові точки і лінії в трикутнику.

          4. Ортоцентр. Пряма Ейлера, коло дев’яти точок.

          5. Опорні задачі про чудові лінії. Графи.

Приклади розв'язування задач на побудову.

Вступ

Геометричні побудови можуть зіграти серйозну роль у математичній підготовці здобувача освіти, тому дана тема є важливою для вчителя математики. Жоден вид задач не дає стільки матеріалу для розвитку математичної ініціативи й логічних навичок учня, як геометричні задачі на побудову. Ці задачі звичайно не допускають стандартного підходу до них і формального сприйняття їх учнями. Задачі на побудову зручні для закріплення теоретичних знань учнів за будь-яким розділом шкільного курсу геометрії. Вирішуючи геометричні задачі на побудову, учень здобуває багато корисних креслярських навичок.

 Даний збірник пропонується  під час підготовки учнів до олімпіад використовувати елементи підготовчого курсу «Розв’язування олімпіадних задач», який має на меті: сприяти досягненню учнями високого рівня математичної підготовки; розвивати стійкий пізнавальний математичний інтерес; поєднати шкільне навчання з дослідницькою діяльністю за вибором, згідно з власним інтересом до конкретних проблем. Геометричні побудови є істотним чинником математичної освіти; вони являють собою потужне знаряддя геометричних досліджень. Теорія геометричних побудов становить теоретичну основу практичної графіки: багато креслярських методів опираються на розв'язки геометричних задач на побудову.

Цілі та завдання:

- підвищення рівня якості знань учнів, розширення математичного кругозору;

- прищеплення інтересу до математики та її застосувань;

- виявлення найбільш обдарованих учнів та розвиток їх творчих здібностей;

- навчання культурі самоосвіти та саморозвитку школярів;

- удосконалення умінь та навичок самостійної роботи учнів зі спеціальної літератури;

- організація діяльності учнів з метою підготовки їх до участі в різних олімпіадах та конкурсах;

- профорієнтація учнів та підготовка їх до отримання подальшої освіти.

ЧАСТИНА  І. ЗАДАЧІ НА ПОБУДОВУ ЗА ДОПОМОГОЮ ЦИРКУЛЯ Й ЛІНІЙКИ

1.  Поняття задачі на побудову

Задача на побудову полягає в тому, що потрібно побудувати наперед зазначеними інструментами деяку фігуру, якщо дана деяка інша фігура й зазначені деякі співвідношення між елементами шуканої фігури й елементами даної фігури.

Кожна фігура, що задовольняє умову задачі, називається розв'язком цієї задачі.

Знайти розв'язок задачі на побудову - значить звести її до кінцевого числа основних побудов, тобто вказати кінцеву послідовність основних побудов, після виконання яких шукана фігура буде вже вважатися побудованою в силу прийнятих аксіом геометрії. Перелік припустимих основних побудов, а отже й хід розв'язку задачі, суттєво залежить від того, які саме інструменти вживаються для побудови.

У будь-якій задачі на побудову потрібно за якими-небудь даними фігурам побудувати шукану фігуру, що задовольняє ті або інші умови. При цьому вказується ( тобто формулюється явно або мається на увазі), за допомогою яких креслярських інструментів слід виконати побудова шуканої фігури. Тут можуть представитися різні комбінації з наступних інструментів: лінійка, косинець, транспортир, циркуль. У шкільному курсі геометрії звичайно розглядаються задачі на побудову за допомогою циркуля й лінійки, тому надалі всюди, де не обговорено противне, передбачається, що всі побудови повинні бути виконані за допомогою цих інструментів.

Передбачається, що лінійка як інструмент геометричних побудов не має масштабних ділень і з її допомогою можна провести пряму, що проходить через дві дані або побудовані точки. Ніяких інших операцій виконати лінійкою не можна. За допомогою циркуля як інструмента геометричних побудов можна описати окружність із центром у даній або побудованій точці й радіусом, рівним даному або побудованому відрізку.

Виберемо в просторі деяку площину й назвемо її основною площиною. Будемо припускати, що всі розглянуті геометричні фігури лежать у цій площині. Точки, прямі й окружності основної площини відіграють особливу роль у задачах на побудову за допомогою циркуля й лінійки, тому їх, ми називаємо основними фігурами. Крім основних фігур, нас будуть цікавити також інші найпростіші фігури: відрізки, промені, кути, півплощини, багатокутники й дуги окружностей. Однак зазначимо, що кожна із цих фігур визначається завданням точок, прямих або окружностей. Наприклад, відрізок АВ визначається точками А и В і прямою АВ. Промінь визначається початком променя ( тобто точкою), прямої, якій він належить, і деякою його точкою. Таким чином, не порушуючи загальності, можна вважати, що у будь-якій геометричній задачі на побудову потрібно за заданими основним фігурам побудувати інші основні фігури (точки, прямі або окружності).

Точки й прямі, як звичайно, будемо позначати відповідно прописними й малими літерами латинського алфавіту (А, В, С, …, а, b, с), кути-(ВОА, A, φ, ψ). Для того щоб у загальному виді сформулювати постановку задачі на побудову, введемо наступні узгодження. Будемо вважати, що при формулюванні й розв'язанні кожної конкретної задачі на побудову за певним правилом виділяється деяка множина Ω основних фігур ( тобто точок, прямих і окружностей), кожний елемент якої називається побудованою фігурою. Кожна пряма або окружність множини Ω розглядається як єдиний об'єкт - елемент множини. Наприклад, якщо γ - побудована окружність, те звідси не випливає, що всі точки окружності побудовані, більше того, ми не припускаємо навіть, що центр окружності γ є окремою точкою. Звичайно, окремі точки цієї окружності як самостійні фігури можуть бути побудованими, але це повинно бути застережене умовами задачі.

Сформуємо у загальному виді постановку задачі на побудову. Дана кінцева множина основних побудованих фігур , , ..., і описана властивість, що характеризує шукану непобудовану основну фігуру Ф. Потрібно, використовуючи аксіоми геометрії, одержати кінцеву множину основних побудованих фігур, що містить фігуру Ф.

При розв'язуванні задач на побудову часто доводиться "довільно вибирати" довільні точки, що як належать, так і не належать побудованим прямим, окружностям, а також відрізкам і променям. Можливість вибору довільних побудованих точок, що належать побудованим прямим або окружностям, не скінченне. Можливість вибору точок, що не належать побудованим прямим і окружностям, можна обґрунтувати за допомогою аксіом геометрії.

2. Схема розв'язування задач на побудову.

Звичайно при розв'язку задач на побудову користуються схемою, яка полягає в наступному (Схема.1). Розв'язок задачі розчленовують на чотири частини: аналіз, побудова, доказ і дослідження. Нижче даний короткий опис кожної із цих частин.

Схема.1

Аналіз або пошук розв'язку задачі полягає у встановленні залежностей між даними фігурами й шуканою фігурою з метою знаходження способу розв'язування задачі.

Для проведення аналізу задачу припускають вирішеної й виконують "від руки" креслення, що зображує шукану й дані фігури. Потім вивчають шукану фігуру і її зв'язку з даними задачі, поки не стане ясна послідовність побудов, що веде до розв'язку. У ряді випадків доцільно виділити точку, пряму або відрізок ( так званий основний елемент побудови), побудова якого приводить до побудови шуканої фігури.

Побудова полягає в послідовнім перерахуванні тих побудов (найпростіших і основних), які треба виконати для розв'язування задачі. При цьому виконується креслення, тобто фактично здійснюється крок за кроком побудова шуканої фігури за допомогою циркуля й лінійки.

Доказ полягає в тому, щоб установити, що побудована фігура дійсно задовольняє всім умовам, поставленим у задачі. У ряді випадків доказ безпосередній випливає з ходу побудови.

Дослідження полягає в тому, щоб відповісти на запитання: 1)Чи при всякому виборі даних задача має розв'язок, тобто шукану фігуру можна побудувати циркулем і лінійкою? 2) Скільки різних розв'язків має задача при кожному можливому виборі даних?

Для визначення числа розв'язків розрізняють два типи задач на побудову.

Перший тип становлять задачі, у яких потрібно визначити положення шуканої фігури щодо деяких з заданих фігур. У цьому випадку дві фігури, що задовольняють умови задачі й відмінні своїм положенням відносно заданих фігур, вважаються різними, якщо навіть вони рівні одна одній.

Другий тип становлять задачі, у яких положення шуканої фігури стосовно даних не відіграє ролі. Інакше кажучи, якщо F1, F2, …, Fk дані фігури, а Ф - шукана фігура, то при будь-якому русі основної площини образ Ф' фігури Ф також буде розв'язком задачі стосовно даних фігур F1, F2, …,Fk . У цьому випадку всі рівні фігури, кожна з яких задовольняє умовам задачі, уважаються як один розв'язок. Прикладом цього типу задач є задача побудови трикутника по трьом сторонам.

Задача. Побудувати трикутник сторони якого відповідно дорівнюють даним відрізкам а, b і с.

Розв'язок. Проведемо яку-небудь пряму й відкладемо відрізок АВ, дорівнює відрізку с. Далі побудуємо дві окружності (А, b) і (В, а). Нехай С - одна із точок перетинання цих окружностей. З'єднавши точки А, С і В, з відрізками, одержимо шуканий трикутник АВС. Виникає питання:чи при будь-яких заданих відрізках а, b і і с задача має розв'язок? Доведемо, що якщо c а й c b, то трикутник АВС,  що задовольняє умовам:АВ =с, ВС= а, СА = b, можна побудувати тоді й тільки тоді, коли с < а+b(1). Насправді, якщо трикутник АВС, що задовольняє умовам задачі, побудований, то по нерівності трикутника АВ < АС + ВР. Звідси випливає, що виконується рівність(1). Обернено, нехай для відрізків а, b і с виконуються нерівності:с а, с b и с < а + b(2).

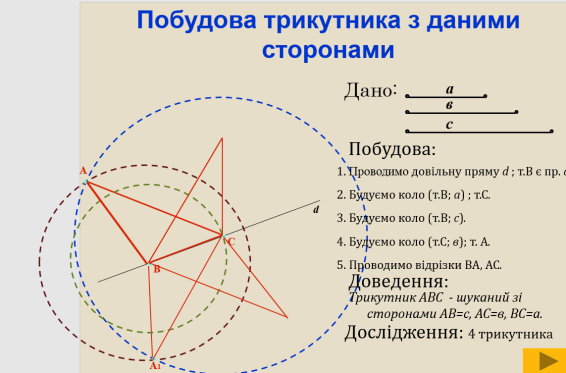Доведемо, що трикутник АВС, що задовольняє умовам задачі, можна побудувати. За побудовою АВ = с, тому АВ < а + b. Але, з іншого боку, якщо, наприклад, a b, те з нeрівностей с а, с b випливає, що с > а – b і АВ > a – b. Таким чином, окружності (А, b) і (В, а) перетинаються у двох точках С и C΄. Легко бачити, що точки А, В и С не лежать на одній прямій. Таким чином, відрізки АВ і ВС і СА утворюють трикутник.

Ясно, що можна побудувати нескінченна множина трикутників, сторони яких відповідно дорівнюють даним відрізкам. Але будь-які два з них рівні по трьом сторонам, тому ми вважаємо, що якщо дана задача на побудову має розв'язок, то вона має тільки один розв'язок.

ЧАСТИНА  ІІ. МЕТОДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ НА ПОБУДОВУ

До основних методів розв'язування задач на побудову відносяться:

1)  Метод геометричного місця точок.

2) Метод перетворення площини (симетрія, паралельне перенесення, поворот, гомотетія).

          3) Алгебраїчний метод.

          4) Чудові точки і лінії в трикутнику (чотирикутнику). Центр вписаного і описаного кіл в трикутнику, чотирикутнику. Центр мас. Золоте правило важеля.

          5) Ортоцентр(точка перетину висот). Центри зовні вписаних кіл.

          6) Пряма Ейлера, коло дев’яти точок. Опорні задачі про чудові лінії. Графи.Перераховані методи є одним з видів застосування на практиці відповідних геометричних понять, які становлять основу кожного з методів. Тому без гарного знання цих понять учнями не може бути ніякої мови про успішне засвоєння відповідних методів. Але, з іншого боку, у силах учителя підібрати таку систему задач на побудову й так побудувати навчання, щоб розв'язувані задачі поглиблювали уявлення й збільшували знання школярів про дане поняття, розкриваючи його з різних сторін. Задачі при вивченні конкретного методу повинні підбиратися так, щоб у них як можна більш яскраво проявлялася суть досліджуваного методу, особливо на первісному етапі його вивчення. При цьому якщо задача вирішується декількома методами, то досліджуваний метод повинен дозволяти розв'язати задачу найбільше економно й красиво. Розглянемо більш докладно кожний метод.

 1. Метод геометричного місця точок

Математична сутність методу геометричного місця точок досить проста. Вона полягає в тому, що шукана точка визначається як точка перетинання деяких двох геометричних місць (або іноді як точка перетинання деякого геометричного місця точок з даною прямою або окружністю); при цьому ті умови задачі, які визначають положення шуканої точки, розчленовуються подумки на дві умови, і кожне з них дає деяке геометричного місця точок, побудова якого виявляється можливою (іноді одне із цих геометричних місць заміняється безпосередньо даною прямою або окружністю).

Метод геометричного місця точок є одним з найважливіших прийомів розв’язування геометричних задач на побудову.

При вивченні цього методу в школі справа, звичайно, полягає не в тому, щоб учні вміли описати суть методу словами, а в тому, щоб учні вміли свідомо користуватися цим методом.

Основа даного методу – поняття геометричного місця точок. Геометричним місцем точок (ГМТ) простору називається множина всіх точок простору, кожна з яких має властивість зазначену вище.

Усі інші точки простору зазначеної властивістю не мають. ГМТ задається властивістю точки, яка називається характеристичною властивістю цього ГМТ (фігури).

Кожна задача, у якій потрібно знайти ГМТ по його характеристичній властивості, припускає описання цього ГМТ наочно через відомі елементарні фігури. Розв'язок задачі на відшукання ГМТ неминуче приводить до доказу двох тверджень – прямого і йому протилежного; необхідно довести, що: 1) кожна точка передбачуваного (шуканого) ГМТ має задану властивість; 2) будь-яка точка, що не належить цій фігурі, заданою властивістю не має.

Набір досліджуваних ГМТ може бути найрізноманітнішим. Традиційний шкільний набір – це:

а) множина всіх точок площини, вилучених від даної токи на дану відстань;

б) множина всіх точок площини, рівновіддалених від двох даних точок;

в) множина всіх точок площини, вилучених від даної прямої на дану відстань;

г) множина всіх точок площини, рівновіддалених від двох даних прямих.

Крім цього до списку по можливості можуть бути додані наступні ГМТ:

а) множина всіх точок площини, з яких даний відрізок видний під даним кутом.

б) множина всіх точок площини, для кожної з яких різниця квадратів відстаней до двох даних точок постійна, дорівнює квадрату даного відрізка;

Розглядати ці ГМТ доцільно тільки в класах з поглибленим вивчанням математики, а також на позакласних заняттях з математики.

Сутність методу геометричних місць полягає в наступному:

а) задача зводиться до побудови деякої точки;

б) з'ясовується, які властивості має дана точка;

в) розглядається одна із властивостей, будується множина всіх точок, що мають цю властивість;

г) береться наступну властивість і так далі;

д) оскільки шукана точка повинна мати всі ці властивості, то вона повинна належати кожній з побудованих множин, тобто належить перетинанню цих множин.

2.Методи геометричних перетворень

Методи цієї групи мають досить багато загального. Кожний вивчається, як правило, при розгляді відповідного перетворення, при цьому розв'язувані задачі служать для закріплення й більш глибокого засвоєння досліджуваного поняття. Для підвищення ефективності навчання необхідно, щоб, крім первісних представлень про саме перетворення, учні вміли виконувати побудову образів фігур при цьому перетворенні, тому що використання образу шуканої фігури при побудові є основою кожного із цих методів, їх основна ідея й суть.

Якщо шукану фігуру відразу побудувати важко, то її перетворюють у яку-небудь іншу фігуру, побудову якої можна зробити легше.

При вивченні цих методів доцільно виділити найбільш характерні ознаки для того, щоб у майбутньому, аналізуючи задачу, учень міг вибрати відповідний метод.

Метод центральної симетрії

Симетрією щодо точки О ( центральною симетрією) Z₀ простору називається перетворення простору, який точку О відображає на себе, а будь-яку іншу точку М відображає на таку точку М₁, якщо точка О є серединою відрізка ММ₁.

Даний метод застосуємо до тим задач, в умові яких зазначена точка, що є центром шуканої симетрії або допоміжної фігури.

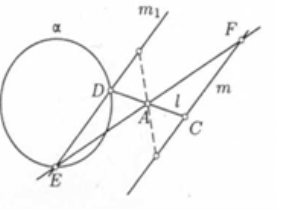
Розглянемо задачу: " Через дану точку А провести пряму так, щоб її відрізок з кінцями на даних прямій і окружності ділився точкою навпіл".

Розв'язок. Нехай m і б — дані пряма й окружність, CD - шуканий відрізок, С m, Dа. Тоді (C) = D. Якщо (m) = m₁, то Dm₁ і, отже, Dа m₁. Звідси випливає така побудова: будуємо образ m₁ прямій m при симетрії , крапки D і Е перетинання прямій m₁ з даною окружністю б визначають разом із крапкою А шукані прямі DA і ЕА .

 Метод осьової симетрії

Симетрією простору щодо даної прямій l (осьова симетрія) називається перетворення, яке кожну точку прямої l відображає на себе, а будь-яку іншу точку М простору відображає на таку точку М₁, якщо пряма l служить серединним перпендикуляром до відрізка ММ₁. Пряма l називається віссю симетрії. Важко вказати загальні ознаки задач, які розв'язуються методом осьової симетрії. Застосування осьової симетрії доцільно для задач, які легко вирішуються, якщо частина даних розташована по одну сторону деякої прямої, а інші – по іншу.

Розглянемо задачу: "Побудувати ромб так, щоб одна з його діагоналей дорівнювала даному відрізку r і лежала на даній прямій а, а інші дві вершини ромба лежали відповідно на даних прямих b і с".

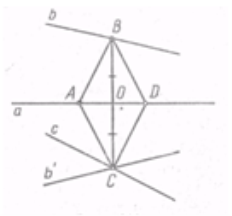Аналіз. Нехай ABDC — шуканий ромб, AD = r. Зауважемо, що задача про побудову ромба зводиться до побудови однієї якої-небудь із його вершин, наприклад вершини С. За властивостями ромба точки В и С симетричні відносно прямої а. Тому при осьовій симетрії відносно прямої а точка В перетвориться в точку С, а, отже, пряма b — у деяку пряму b', що проходить через точку С. Таким чином, точка С може бути побудована як точка перетину прямих с і b', з яких одна дана, а інша легко будується.

Побудова. Будуємо послідовно: пряму b', симетричну із прямій b відносно прямої а; точку С, загальну для прямих с і b'; пряму ВС; точку ОВС а; точки А и D на прямій а, що знаходяться від точки О на відстані ; ABCD — шуканий ромб. Дослідження. Можливі наступні випадки: 1) с || b', розв'язків немає; 2) с b', розв'язків нескінченно багато; 3) прямі с і b' перетинаються поза прямою а, один розв'язок; 4) прямі с і b' перетинаються на прямій а, розв'язків немає .

 Метод паралельного переносу

Паралельним переносом на вектор називається відображення площини на себе, при якому кожна точка М відображається в таку точку М₁, що вектор дорівнює вектору .

Методом паралельного переносу вирішують задачі, при аналізі яких важко знайти залежність між даними елементами, що дозволяє побудувати шукану фігуру, але якщо ми яку-небудь частину або всю фігуру перенесемо паралельно в деякому напрямку на певну відстань, то одержимо допоміжну фігуру, яку легко можна побудувати. Напрямок і величина переносу визначаються так, щоб у допоміжну фігуру ввійшло більше число даних.

Розглянемо задачу: "Побудувати опуклий чотирикутник, знаючи три його кути й дві протилежні сторони".

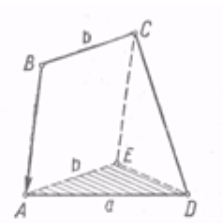Докладніше: дано два відрізки а й b і три кути б, в, д. Потрібно побудувати чотирикутник ABCD так, щоб А = б, В = в, D = д, AD = a, СВ = b. Передбачається, що 0° < б < 180, 0° < в < 180, 0°< д < 180°.

Аналіз. Допустимо, що ABCD— шуканий чотирикутник. Перенесемо сторону ВС на вектор, і нехай відрізок ВС займе після переносу положення АЕ. Тоді в AED відомі: AD = a, AE = b, DAE = BAD – BAE = A – (180° – B) = б + в – 180°. За цим даними AED може бути побудований.

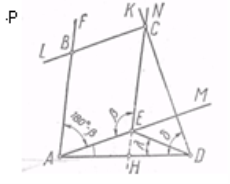Побудова. 1) На довільній прямій будуємо відрізок AD = а ; 2) Через точку А проводимо промінь AM під кутом б + в – 180° до променя AD; 3) Відкладаємо на промені AM відрізок АЕ = b; 4) Будуємо промінь EN, що утворює з ЕА кут в й розташований із точкою D по різні сторони від прямої AM; 5) Будуємо промінь DK так, щоб ADK був рівний д і щоб промінь DK розташовувався по ту ж сторону прямщї DE, що й промінь EN; 6) Відзначаємо точку С перетинання променів EN і DK — третю вершину чотирикутника; 7) Четверта вершина В знаходиться з перитинання прямої AF, паралельної СE, із прямої CL, паралельної АЕ.

Доказ. BAD = ВАЕ+ DAE = (180° – в) + (б + в – 180°) = б. ABC = СЕА, як кути, сторони яких відповідно паралельні й протилежно спрямовані. СЕА = в за побудовою. ADC = д за побудовою. Відрізок AD = а за побудовою. Але АЕ = b, а виходить, і ВС = b .

Метод повороту

Поворотом площини навколо точки О на кут називається відображення площини на себе, при якому кожна точка М відображається в таку точку М₁, що ОМ = ОМ₁ і кут МОМ₁ = .

Даний метод застосовується до тих задач, де або частини фігур зближаються в положення, зручне для побудови, або при заданих явно або не явно центрі й куті повороту потрібно відшукати дві відповідні точки, що лежать на даних або шуканих фігурах.

Розглянемо задачу: "Земельна ділянка квадратної форми була обгороджена. Від огорожі збереглися два стовпи на паралельних сторонах квадрата. Крім того, залишився стовп у центрі квадрата. Потрібно відновити границю ділянки".

Аналіз. Нехай ABCD — шуканий квадрат, О — його центр, М і N- дані точки відповідно на сторонах АВ і CD . Якщо повернути квадрат на 180° близько його центру О, то він перетвориться сам у себе. Точка М займе деяке положення М' на стороні CD, а точка N — деяке положення N' на стороні АВ. Після цього неважко вже побудувати прямі АВ і CD і відновити шуканий квадрат.

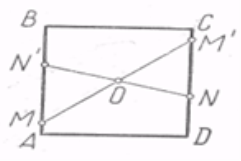Побудова. 1) Будуємо точку М', симетричну М відносно О, і точку N', симетричну N відносно О. 2) Будуємо прямі MN' і NM'. 3) Повернемо побудовані прямі близько точки О на 90°. Чотири побудовані прямі обмежують шуканий квадрат.

Доказ опускаємо.

Дослідження. За змістом задачі неможливий випадок, коли точки М і N розташовуються із точкою О на одній прямій, але не симетричні відносно О. Якщо точки М і N симетричні відносно О, то задача стає невизначеною. В інших випадках задача має єдиний розв'язок .

3. Чудові точки і лінії в трикутнику .

Чудові точки трикутника - точки, місце розташування яких однозначно визначається трикутником і не залежить від того, в якому порядку беруться сторони і вершини трикутника.

Чудовими точками трикутника є точки перетину:

• Медіан - центроид, центр мас;
• Биссектрис - інцентр, центр вписаного кола;
• Висот - Ортоцентр;
• Серединних перпендикулярів - центр описаної окружності;
• Cімедіан - точка Лемуана;
• Биссектрис серединногоHYPERLINK "http://znaimo.com.ua/%D0%A1%D0%B5%D1%80%D0%B5%D0%B4%D0%B8%D0%BD%D0%BD%D0%B8%D0%B9_%D1%82%D1%80%D0%B8%D0%BA%D1%83%D1%82%D0%BD%D0%B8%D0%BA" трикутника (його інцентра) - точка Шпікера;
• Точки перетину відрізків, що з'єднують вершини трикутника:
• c точками дотику протилежних сторін і вписаного кола - точка Жергонна;
• c точками дотику протилежних сторін і вневпіHYPERLINK "http://znaimo.com.ua/%D0%92%D0%BD%D0%B5%D0%B2%D0%BF%D1%96%D1%81%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D1%96%D1%81%D1%82%D1%8C"саннойHYPERLINK "http://znaimo.com.ua/%D0%92%D0%BD%D0%B5%D0%B2%D0%BF%D1%96%D1%81%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D1%96%D1%81%D1%82%D1%8C" окружності - точка Нагеля;
• c відповідними вільними вершинами рHYPERLINK "http://znaimo.com.ua/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D0%B8%D0%B9_%D1%82%D1%80%D0%B8%D0%BA%D1%83%D1%82%D0%BD%D0%B8%D0%BA"івностороннього трикутника, побудованих на сторонах трикутника (назовні) - перша точка Торічеллі
• з відповідними вільними вершинами правильних трикутників, побудованих всередину трикутника - друга точка Торічеллі.
• c відповідними вільними вершинами трикутників, подібних вихідного трикутника і побудованих на його сторонах - точки Брокар;
• Центр окружності HYPERLINK "http://znaimo.com.ua/%D0%9A%D0%BE%D0%BB%D0%BE_%D0%B4%D0%B5%D0%B2%D1%8F%D1%82%D0%B8_%D1%82%D0%BE%D1%87%D0%BE%D0%BA"дев'ятиHYPERLINK "http://znaimo.com.ua/%D0%9A%D0%BE%D0%BB%D0%BE_%D0%B4%D0%B5%D0%B2%D1%8F%D1%82%D0%B8_%D1%82%D0%BE%D1%87%D0%BE%D0%BA" точок.

БаріцентриHYPERLINK "http://znaimo.com.ua/%D0%91%D0%B0%D1%80%D1%96%D1%86%D0%B5%D0%BD%D1%82%D1%80%D1%96%D1%87%D0%B5%D1%81%D0%BA%D1%96%D0%B5_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D0%B8"чніHYPERLINK "http://znaimo.com.ua/%D0%91%D0%B0%D1%80%D1%96%D1%86%D0%B5%D0%BD%D1%82%D1%80%D1%96%D1%87%D0%B5%D1%81%D0%BA%D1%96%D0%B5_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D0%B8" координати центру, записані через сторони (або тригонометричні функції кутів) трикутника, дають можливість перевести багато завдань про центри трикутника на алгебраїчний мову. Наприклад, з'ясувати, задають чи два визначення один і той же центр або лежать чи то три даних центру на одній прямій.

•     Розглядають пари центрів. Наприклад
•                 точки  Брокар.
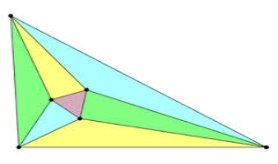
•                 Точки Аполлонія. Для всякого ненародженого трикутника АВС можна побудувати окружність Аполлонія до сторони АВ, що проходить через точку С. Окружності, побудовані таким чином до трьох сторін, будуть перетинатися у двох точках - внутрішньої і зовнішньої Аполлонія відповідно.

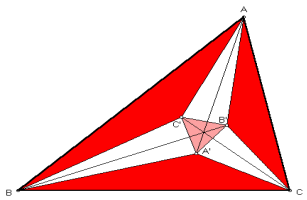
Точки й лінії пов'язані з трикутником

        Є сотні різноманітних побудов для визначення особливих точок всередині трикутника, які задовольняють деякі унікальні умови (дивись в списку посилань перелік статей). Часто необхідно побудувати три прямі, що пов'язані аналогічно із трьома сторонами (вершинами, кутами) трикутника і тоді переконатись, що вони перетинаються в одній точці. Важливим інструментом для перевірки цього є теорема Чеви, яка дає критерії для визначення конкурентності прямих. Подібно до цього, лінії пов'язані з трикутником часто будуються після перевірки, що три аналогічним чином отримані точки є колінеарні — теорема Менелая дає для цього випадку загальний критерій. В цьому розділі приведені тільки такі побудови, що найбільш часто зустрічаються.

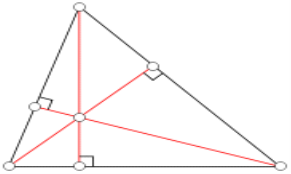
Три висоти трикутника перетинаються в ортоцентрі

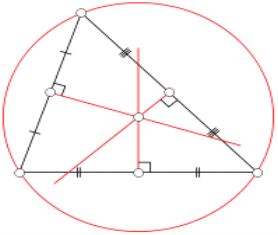
Центр  описаного кола

      Серединний перпендикуляр трикутника — це перпендикуляр, який проходить посередині сторони трикутника. Три серединні перпендикуляри перетинаються в одній точці, яка є центром описаного кола. Діаметр описаного кола можна визначити з теореми синусів.

Виходячи з теореми Фалеса можна стверджувати — якщо центр описаного кола розміщений на одній із сторін трикутника, тоді протилежний кут прямий. Більше того, якщо центр описаного кола знаходиться всередині трикутника, то трикутник гострокутний, а якщо назовні — то трикутник тупокутний.

     Висота трикутника — пряма проведена з вершини і перпендикулярна до протилежної сторони або до продовження протилежної сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра

називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника. Три висоти перетинаються в одній точці, яка назвається ортоцентром трикутника.

4.Ортоцентр. Пряма Ейлера, коло дев’яти точок.

Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут). Дивіться також ортоцентрична система                                                       

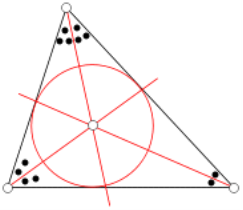
На перетині трьох бісектрис трикутника знаходиться центр вписаного кола.

Бісектриса трикутника — це пряма проведена через вершину, яка ділить відповідний кут на дві рівні частини. Три бісектриси перетинаються в одній точці, інцентрі, центрі вписаного в трикутник кола. Вписане коло — це коло, яке лежить всередині трикутника і дотикається до трьох його сторін. Крім того є ще три важливі кола, зовнівписані; вони лежать за межами трикутника і дотикаються до одної його сторони, а також до продовження інших двох. Центри внутрішнього і зовнішніх вписаних кіл утворюють ортоцентричну систему. Пряма Е́йлера, названа на честь Леонарда Ейлера, — пряма, яку можна провести в будь-якому нерівносторонньому трикутнику; вона проходить через кілька важливих визначених для трикутника точок. На малюнку пряма Ейлера показана червоним. Вона проходить через ортоцентр (синій), центр описаного кола (зелений), центроїд (помаранчевий), і центр кола дев’яти точок (червоний) трикутника.

Ейлер (1767) показав, що в будь-якому трикутнику, ортоцентр, центр описаного кола і центр кола дев’яти точок лежать на одній прямій. В рівносторонньому трикутнику ці точки збігаються, але в будь-якому іншому трикутнику ні. Центр кола дев’яти точок лежить посередині між ортоцентром і центром описаного кола, а відстань від центроїда до центра описаного кола дорівнює половині відстані від центроїда до ортоцентра.

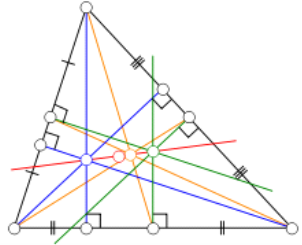
Лінія  Ейлера

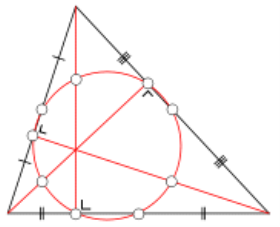
Коло дев'яти точок.

       Середні точки трьох сторін і основи трьох висот всі лежать на одному колі, яке називається колом дев'яти точок трикутника. Решта три точки, через які коло отримало свою назву, це середини тієї частини висоти, що лежить між ортоцентром і вершиною. Радіус кола дев'яти точок дорівнює половині описаного кола. Воно дотикається до вписаного кола (в точці Феєрбаха) та до трьох зовнівписаних кіл. Центроїд (жовтий), ортоцентр (синій), центр описаного кола (зелений) і центр кола дев'яти точок (червона точка) всі лежать на одній лінії, яка називається лінія Ейлера (червона лінія). Центр кола дев'яти точок лежить на середині між ортоцентром та центром описаного кола, а відстань між центроїдом і центром описаного кола дорівнює половині відстані між центроїдом та ортоцентром.

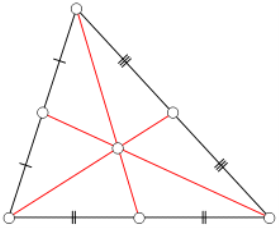Центроид - точка перетину медиан в трикутнику. Центроид традиційно позначається латинською буквою M .

У трикутнику

•     Центроїд ділить кожну медіану щодо 2:1, рахуючи від вершини.
•     Центроїд лежить на відрізку, що з'єднує Ортоцентр і центр описаного кола, і ділить його у відношенні 2:1 (див. пряма Ейлера).
•     Якщо у вершини трикутника помістити рівні маси, то центр мас ( барицентра) отриманої системи буде збігатися з центроїдів. Більше того, центр мас трикутника з рівномірно розподіленим масою також знаходиться в центроїда.
•     Зокрема, якщо M - Центроїд трикутника A B C то для будь-якої точки O вірно, що точка перетину медіан є точкою, для якої сума квадратів відстаней до вершин трикутника .

 Факт, що три медіани перетинаються в одній точці, був доведений ще Архімедом. має найменше значення ( теорема Лейбніца).

Галактика Трикутника ( M 33, NGC 598) - спіральна галактика типу Sc у сузір'ї Трикутника. Третя за величиною після Галактики Андромеди і Чумацького Шляхугалактика місцевої групи, в 5-10 разів менше Чумацького Шляху за масою. По діаметру в 2 рази менше Чумацького Шляху і в 4 рази менше галактики Андромеди. Її діаметр - близько 50 тис. св. років відповідає середній величині, типової для спіральних галактик.

В одному з її спіральних рукавів знаходиться емісійна туманність NGC 604 поперечником 1300 св. років - найбільша відособлена область зореутворення, де зосереджено більше 200 зірок-гіпергігантов.

5.Опорні задачі про чудові лінії. Графи.

Граф -  це сукупність кінцевого числа точок і ліній, що попарно сполучають деякі з цих точок  (є більш строге визначення, але на практиці воно не потрібне). Ці точки називаються вершинами, а лінії, що сполучають їх, називаються ребрами графа або дугами графа.

 Число ребер, що виходять з вершини графа називають степінью цієї вершини. Вершина графа, що має непарну степінь, називається непарною, а що має парну степінь  парною.

 Розглянемо задачу, яка дає уявлення про використання теорії графів.

Задача 1.

А, Б, В і Г – друзі. Один з них – лікар,  інший – журналіст, третій  – тренер спортивної  школи і четвертий будівельник. Журналіст написав  статті про А і Г. Тренер і журналіст разом з Б ходили в похід. А і Б були на прийомі у лікаря. У кого яка професія?

Запишемо хід рішення:

     1)  Б- не лікар,                       А                                    Лікар

           Б- не журналіст

           Б – не тренер                         Б                                           Журналіст

           Б – будівельник.

2. А – не будівельник

           А – не лікар,                               В                                      Тренер

           А – не журналіст

           А – тренер.

3. Г – не будівельник,                      Г                                      Будівельник

           Г- не тренер

           Г- не журналіст

           Г – лікар.

     4)   В – журналіст.

 Задача  2                                                     Задача 3   

                                                                    А                             Б

                                                                В                                Г

Відповідь: 10 рукостискань                                         Відповідь: 12 фотографій

Розглянемо основні правила і теореми теорії графів, без яких  неможливе розв'язування задач.

Розглянемо застосування цього правила при розв'язуванні задач.

Задача 4.

      У  Тернопольській  області треба встановити 15 веж. Чи можна вежі  з'єднати проводами так, щоб кожна вежа була сполучена рівно з п'ятьма іншими?

Рішення.

    Допустимо це можливо. Розглянемо граф, вершини якого – вежі, а ребра – сполучаючі дроти. У цьому графові 15 вершин, ступінь кожної з яких дорівнює 5. Підрахуємо кількість ребер в цьому графові. Для цього підсумуємо ступені його вершин. Ясно при такому підрахунку кожне ребро враховане двічі (адже воно сполучає дві вершини)

Тому число ребер повинно  дорівнювати  (15·5):2.  Але це число не ціле!

Тому такого графа не існує і з'єднати вежі необхідним чином неможливо.

 Задача  5.

    Чи можна організувати такий турнір, щоб у  ньому  брали участь 40 команд і кожна команда зіграла рівно 3 матчі?

Рішення.

    Позначимо кожну команду точкою ( вершина графа), а кожний матч,зіграний двома командами, -  дугою, яка сполучає ці точки ( ребра графа). Тоді з кожної точки  має виходити три ребра. Підрахуємо кількість ребер. Це і буде кількість всіх зіграних  ігор:

                                          ( 40·3):2=60- число ціле.

   Відповідь: такий турнір організувати  можна.

 Тепер застосуємо до розв'язування задач слідство: сума ступенів всіх вершин графа – число парне.

Задача 6.

Є 30 осіб, сере яких деякі знайомі між собою. Доведіть, що кількість осіб, які мають непарну кількість знайомих, парна.

Рішення.

    Розглянемо граф : кожна людина –  це вершина, кожне знайомство двох  осіб – це ребро.Одже, у нас граф з 30-тьма вершинами.  Біля кожної вершини напишемо по числу – кількості ребер, що виходять з неї ( степінь вершини). Степінь кожної вершини покаже число знайомих кожної з тридцяти  осіб. Тоді сума всіх цих чисел – число  парне  ( по слідству з правила 1 ). Оскільки сума парних вершин – число парне, то і сума непарних вершин повинна бути парною. Доказано.

Теорема про парність непарних вершин займає центральне місце в теорії графів. Важливо навчитися застосовувати її при розв'язуванні задач.

Задача 7.

   У класі 30учнів. Чи може бути так, що 9 з них мають по 3 друзів ( у цьому класі), 11 – по 4 друга, а 10 – по 5 друзів.

Рішення.

    Якби це було можливо можна було б намалювати граф  з  30 вершинами, 9   з них мали б степінь 3, 11 – степінь  4,  10 -  степінь – 5. Виходить,що у такого графа  19 непарних вершин  А це неможливо по теоремі 1.

Одже, такої  ситуації бути не може. 

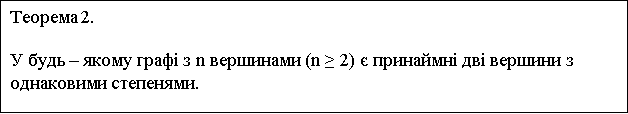
Задача 8.

   Група, що складається з  n школярів, обмінюється фотографіями. У деякий момент часу з'ясовується, що двоє зробили однакове число обмінів. Довести, що  серед школярів є той, хто  ще  не почав обміну, або один , який вже зробив його.

 Рішення.

    Розглянемо граф: школярі – вершини графа, фото, якими вони обмінюються, – ребра. Степінь кожної вершини –це  кількість фотографій,які  обміняв цей школяр. Хай кожен обміняв різну кількість фотографій.  А- не обмінював фото, В - обміняв 1 фото, С-2, і т.д.то останній  Е обміняв (n-1)  фото, а цього бути не може. Оскільки  тоді  він виходить  обмінявся і з школярем А, але за припущенням  А ні з ким не обмінювався.

1. Якщо пару будь-якій вершині складе вершина Е, то видно, що  вершина А ізольована, тобто  є  учень, що ще не почав обміну.

       2) Якщо пару будь-якій вершині складе вершина А, то вершина Е сполучена з всіма іншими,тобто є учень, що вже закінчив обмін. Доказано.

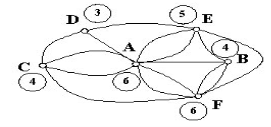
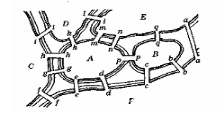
Ззадача  про 15 мостів.

  У деякій місцевості через протоки перекинуто 15 мостів.

Чи можна обійти всі мости пройшовши по кожному тільки один раз?

Рішення:

Побудуємо граф, де вершини - острови і береги, а ребра - мости.

Непарні вершини: D, E.

Одже,оскільки кількість непарних вершин  дорівнює  2, то обхід можливий.

Його початок може бути в місцевості D, а кінець в місцевості E.

 Теорія графів дозволяє швидко і витончено вирішувати завдання, які вельми важко вирішити іншими методами. Також  дає можливість розв'язувати не одну окремо взяту задачу, але і знаходити методи рішення цілого класу задач.

Приклади розв'язування задач на побудову

Задача.

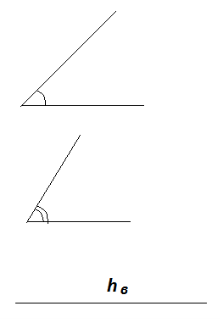
Побудувати трикутник, знаючи два його кути А і С і  висоту h, проведену до сторони АС.

Розв'язок.

Відкидаємо умову, що визначає розміри трикутника і за умовою, що залишилась, будуємо трикутник , подібний даному. Потім враховуємо задану висот, вибираємо центр подібності і перетворюємо побудований трикутник в шуканий.

Дано:

Побудова:

Будуємо трикутник А₁В₁С₁ по двом даним кутам і який буде подібний даному. Проводимо в ньому висоту В₁Д₁. Даний трикутник потрібно перетворити так, щоб висота була рівна h. За центр подібності виберемо точку В₁ і від неї відкладаємо відрізок В₁Д=h. Проводимо пряму САIIС₁А₁ через точку Д.

 АВС – шуканий.

Розглянемо задачу, в якій розміри шуканої фігури визначаються не довжиною відрізка, а сумою чи різницею відрізків.

Задача .

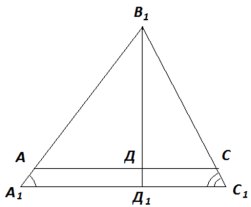
Побудувати трикутник за двома кутами і сумою основи і висоти на основу.

Дано:

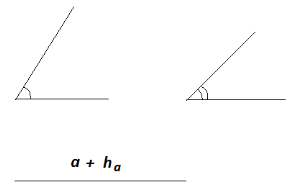
Побудова:

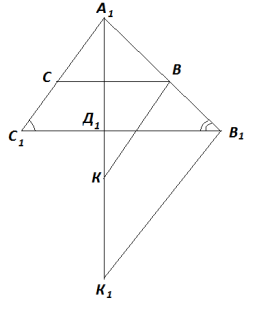Побудуємо по двом даним кутам   А₁В₁С₁, подібний шуканому. Проведемо висоту А₁Д₁. На продовженні висоти А₁Д₁ відкладемо відрізок, рівний основі С₁В₁. Одержимо відрізок А₁К₁, що дорівнює сумі висоти і основи. З'єднаємо точки К₁ і В₁. За центр подібності візьмемо точку А₁ і від неї відкладаємо відрізокА₁К=а+h. Через точку К проводимо пряму, паралельну прямій К₁В₁, одержимо точку В – вершину шуканого трикутника. Проводимо ВС II В₁С₁. Одержимо трикутник А₁ВС – шуканий.

2. Осьова симетрія – це найперше перетворення, з яким учні зустрічаються в геометрії. Спочатку розглядаємо прості задачі: як побудувати точку, симетричну даній; відрізок, симетричний даному і т.п. Потім можна розглянути задачу на побудову,  яка потребує застосування методу осьової симетрії.

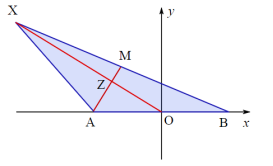
Задача.

   На прямій МN знайти точку X, щоб сума відстаней від даних точок А і В була найменшою. Точки А і В лежать в одній півплощині відносно прямої МN.

Розв'язок.

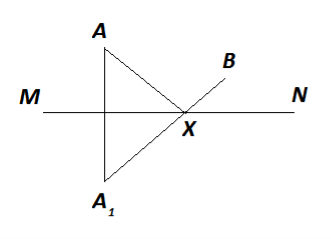
1) Будуємо точку А₁, симетричну точці А, відносно прямої МN.

2)  З'єднуємо точки А₁ і В_.

3) Точку перетину прямих МN і А₁В позначимо X.

4) Точка X – шукана. Відстань АX+XВ – найменша.

3. Розв'язування задач на побудову за допомогою центральної симетрії можна почати з такої задачі.

Задача.  Побудуйте відрізок, середина якого є дана точка , а кінці належать двом даним прямим.

Побудова:

Нехай дано прямі МN, РК і точка А.

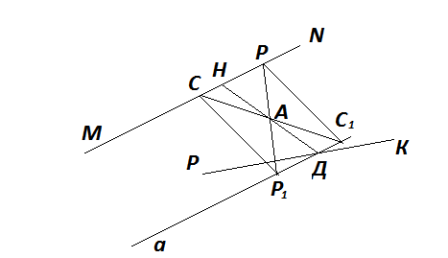
Будуємо пряму, симетричну одній з даних, наприклад МN, відносно даної точки А. Одержимо пряму а, а II МN. Точка Д – точка перетину прямих РК і а. СР₁С₁Р – паралелограм, тому відрізок ДН  ділиться точкою А навпіл. ДН – шуканий.

Потім бажано розглянути складніші задачі. Наприклад :

Задача.

Дано два кола, які перетинаються в точках Р і К. Проведіть через точку К пряму так, щоб дані кола відтинали на ній рівні відрізки.

Вказівка. Побудуйте коло, симетричне одному з даних кіл відносно точки К. При розв'язуванні задач інколи використовується метод повороту на довільний кут, а потім застосовується центральна симетрія.

Задача.

Побудувати рівносторонній трикутник, одна вершина  якого знаходиться в даній точці  А, інша – на даній прямій МД, а третя – на даному колі з центром в точці О.

(Вказівка. Виконаємо поворот навколо точки А сторони АВ і кола з центром в точці О на кут 60°.Точка В співпаде з точкою С.)

4. При розв'язуванні задач методом геометричних місць потрібно починати з задач, умова яких вказує на те єдине геометричне місце, за допомогою якого задача буде розв'язана .

Наприклад: на прямій, перетинаючій сторони кута, знайти точку, рівновіддалену від сторін цього кута.

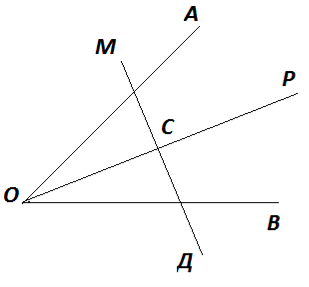
Шукана точка лежить на прямій МД і рівновіддалена від кута. Точка С – точка перетину прямих ОР і МД. Потім переходимо до задач, які потребують для знаходження точки побудови двох геометричних місць.

Задача.

Дано кут і точка М в середині кут. Знайти таку точку, яка була б однаково віддалена від обох сторін кута і віддалена від точки М на дану відстань а.

Розв'язування.

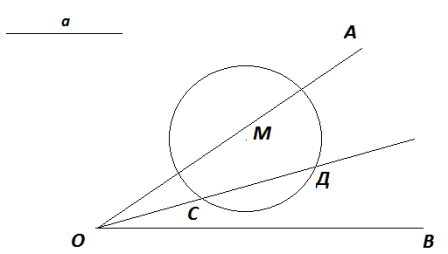
1.Учні самі можуть вказати, що шукана точка знаходиться на бісектрисі даного кута. Отже, будуємо бісектрису даного кута.

2. Звертаємо увагу учнів на те, що шукана точка повинна бути віддалена від точки М на відстань а. А всі точки, рівновіддалені на відстань а, лежать на колі радіуса а з центром в точці М. Будуємо таке коло. Точки С і Д – шукані, так як ці точки лежать і на одному і на другому геометричних місцях. Розв'язок залежить від величини відрізка а і від положення точки М. Задача може мати два розв'язки, один і ні одного.

Корисно розв'язувати простіші задачі і  для економії часу не проводити доведення і дослідження. Такі задачі займають не більше 2-3 хв. і дозволяють краще засвоїти поняття геометричного місця точок.

Наприклад:

             1.Знайти точку, що знаходиться на даній відстані від даної точки .

              2.Знайти геометричне місце точок, які віддалені   від даної прямої на дану відстань.

              3.Знайти геометричне місце вершин трикутників, що мають спільну основу і дану висоту.

Доцільно в класі розв'язати таку задачу:

Задача.

Поділити навпіл кут , вершина якого не розміщена на малюнку.

Розв'язок.

Розв'язків цієї задачі може бути декілька. Розглянемо один із них.

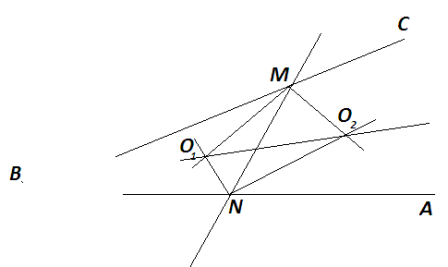
Проведемо довільну пряму , яка перетинає ВС і АВ в точках М і N. Побудуємо бісектриси МО₁, NО₁, МО₂ і NО₂ одержаних кутів ВМN,  МNВ,  NМС,  АNМ. Точки перетину О₁ і О₂ відповідних бісектрис будуть рівновіддалені від ВС і ВА, а тому лежать на бісектрисі кута АВС. Пряма О₁О₂ – шукана пряма.

6. З методом паралельного перенесення доцільно знайомити учнів при вивченні теми "Чотирикутники". Тут можна розв'язувати і задачі обчислювального характеру, і на доведення, і на побудову методом паралельного перенесення. Наприклад,  при розв'язуванні задачі, в якій потрібно довести, що в рівнобедреній трапеції кути при основі рівні, ми проводимо пряму, паралельну бічній стороні і використовуємо властивість рівнобедреного трикутника.

Задачу на побудову можна розглянути таку .

Задача.

Побудувати трапецію за чотирма сторонами а , b , c, d , де а і c основи , b і d – бічні сторони.

Розв'язок.

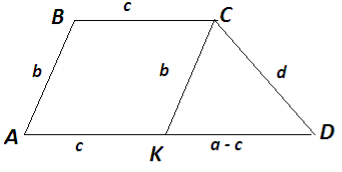
Малюємо довільну трапецію АВСД і відмічаємо на ній відомі елементи. Виконаємо паралельне перенесення АВ, одержимо СК II АВ, СК = АВ. Одержимо трикутник СКД, в якому СК = b, СД = d, КД = а – c і будуємо його за трьома сторонами, а потім добудуємо і трапецію.

Інколи при розв'язуванні задач потрібно паралельно переносити не окремі частини фігури, а всю фігуру .

Задача.

Через два рівнобедрених трикутника , основи яких знаходяться на одній прямій , провести пряму , паралельну основам так , щоб відрізки цієї прямої, які містяться всередині трикутників , були рівні між собою.

Розв'язок.

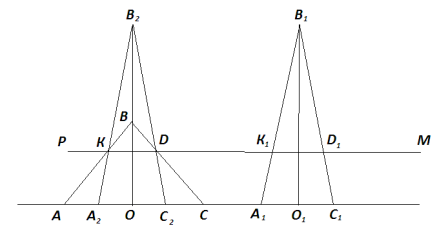
Виконуємо паралельне перенесення трикутника А₁В₁С₁ так, щоб вісь симетрії одержаного трикутника А₂В₂С₂ співпадала з висотою трикутника АВС, тобто з ВО. Точки перетину бічних сторін трикутників  АВС  і А₂В₂С₂ будуть К і Д. Пряма РМ проведена через ці точки – шукана пряма. КД = К₁Д₁.

Задача має один розв'язок, якщо висота першого трикутника менша висоти другого,  а основа першого, навпаки, більша основи другого.  Задача не матиме розв'язку,  якщо і основа і висота одного трикутника будуть менше висоти і основи другого трикутника,  або коли висоти рівні,  а основи не рівні.

Якщо висоти і основи обох трикутників рівні, то трикутники співпадуть і задача матиме безліч розв'язків.

6. Алгебраїчний метод розв'язування задач на побудову розглядається як застосування алгебри до геометрії. Суть цього методу:

а) Припустимо, що задача розв'язана,  робимо малюнок і вводимо позначення невідомого елемента .

б) Із умови задачі, користуючись відомими геометричними співвідношеннями, складаємо рівняння або систему рівнянь.

в) Розв'язуємо рівняння або систему рівнянь .

г) Будуємо шукані відрізки, виражені одержаними формулами через дані відрізки і добудовуємо шукану фігуру .

Задача .

Дано півколо АМВ з діаметром АВ=2R і два півкола на діаметрі з радіусом .  Побудувати коло, яке дотикається до трьох даних півкіл.

Розв'язування.

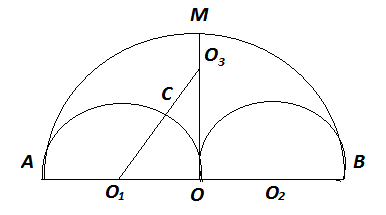
Нехай центр шуканого кола О₃. Позначимо радіус шуканого кола за  x. О₃М = x. З'єднаємо точки О₃ і О₁.

З трикутника О₁О₃О за теоремою Піфагора:

О₁О₃² = О₁О² + ОО₃²

О₁О₃ = ОС + СО₃ = + х; ОО₁ =  ; ОО₃ = R – х;

( + х )² = ()² + ( R – х )² ; + Rх + х² = + R² - 2Rх;

3Rх – R² = 0; R ( 3R – R ) = 0;

R 0    3х – R = 0

Х =  .

Отже, шукане коло ми будуємо з радіусом  .

Побудова очевидна.

Задача  .

Вершини трикутника з сторонами  а, b, с є центрами трьох кіл . Побудувати ці кола  так, щоб вони дотикались одне до одного зовні .

Розв'язок.

Виконуємо малюнок до даної задачі.

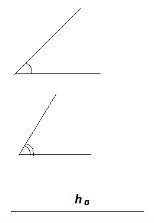
За умовою АВ = с,

ВС = а, АС = b. Нехай радіус кола з центром в точці А дорівнює х, АМ = х. Тоді радіуси двох інших кіл с – х  і  b – х. Так як ВМ = ВN = с – х, а NС = СК = b – х, то ВС = с – х + b – х.

Маємо рівняння  с – х + b – х = а; х =.

Будуємо відрізок х, а потім трикутник за трьома сторонами.

Далі будуємо три кола, знаючи їх радіуси.

З вище  викладеного  досвіду можна  зробити наступні    висновки.

    Для формування в учнів умінь розв’язувати задачі на побудову  доцільно дотримуватись такої послідовності дій:

− ознайомлення учнів із загальною схемою розв’язування задач на побудову проводити поступово, поетапно (аналіз, побудова, доведення і дослідження);

− виконувати на побудову геометричні фігури, застосовуючи набуті раніше знання із різних розділів геометрії;

− будувати ескіз фігури, що відповідає шуканій, розібратись за допомогою цього малюнка в даних і шуканих елементах, намітити план побудови, потім виконати побудову з коротким поясненням.