Збірник завдань для підготовки до ЗНО з математики

Бібліотека Математика 11 клас Контрольні роботи
Про матеріал

Збірник завдань для підготовки до ЗНО з математики.

Збірник укладений відповідно до чинної програми з математики для середньої загальноосвітньої школи (рівень стандарту).

Він призначений для підсумкового контролю навчальних досягнень учнів, а також для підготовки до ЗНО з математики. У ньому 10 завдань у формі комплексної контрольної роботи. Кожне завдання подано у трьох варіантах.

Призначено для учителів математики.

Перегляд файлу

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     Збірник  укладений відповідно до чинної програми з математики для середньої загальноосвітньої школи (рівень стандарту).

     Він призначений для підсумкового контролю навчальних досягнень учнів, а також для підготовки  до  ЗНО  з математики.  У ньому 10 завдань у формі комплексної  контрольної  роботи. Кожне завдання подано у трьох  варіантах.

     Призначено для  учителів математики.

 

 

 

 

 

       Приморськ

             2018

 

 

Завдання № 1

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Яке з наведених тверджень

   є неправильним?

 

А. Функція y=13 - x4 є парною.

Б. Функція y=12 x3 є непарною

В. Функція y=8 x2 зростає на

     множині дійсних чисел.

Г.Функція y= спадає на всій

    області визначення .

 1. Знайдіть область визначення  функції

 f (x) =

   А.

   Б.    

   В.

   Г. 

 

1. Яку  з наведених

    властивостей має

   функція  y = 3 – х2 ?

 

  А. Спадає на множині R.

   Б.  Парна.

   В.  Зростає на множині R.

   Г.  Непарна.

 

2. Яка з наведених рівностей

    правильна?

   А.  = 9

   Б.   = 2

 

   В.    = 2

 

   Г.    = 27

 

2. Яка з наведених рівностей

    правильна?

   А.  = 4

   Б.   = - 1

 

   В.    = 0,2

 

   Г.    = 8

 

2. Яка з наведених

    рівностей правильна?

   А.  = 9

   Б.   = 0,2

   В.    = - 1

 

   Г.    =

 

3. Розв’яжіть рівняння:         .

 А.    х =2;    

 Б.    х = 3; 

 В.    х = 216 ; 

 Г.    х = -3.

 

3. Розв’яжіть рівняння:  

    2х = 8.

А. х = 3; 

Б. х = 0,25;  

В. х = 4;  

Г. х = -3.

3. Розв’яжіть рівняння:

    

 А.    х = 1;    

 Б.    х = - 5; 

 В.    х = - 1 ; 

 Г.    х = 0.

4. Знайдіть 25% від числа

    400.

А. 40;               Б. 200;               В. 25;               Г. 100.

 

4. Знайдіть 25% від числа

    600.

А. 60;               Б. 150;               В. 25;               Г. 300.

 

4.Знайдіть 25% від числа

    900.

А. 90;               Б. 300;               В. 225;             Г. 100.

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

  1.  Із 24 олівців, що лежать у

    коробці, п’ять червоних,

    чотири синіх, а решта –

    прості. Яка ймовірність того,

    що навмання вибраний

    олівець буде простим?

А. ;  Б. ;В. ; Г.

1. У коробці є 40 кульок,

    половина з яких чорного

    кольору. Навмання беруть

    одну з них. Яка ймовірність

    того, що вона чорного

    кольору?

А. ;  Б. ;В. ; Г.

1. У шухляді лежить 9

    хустинок, з яких дві – білого

    кольору. Навмання беруть

    одну з них. Яка ймовірність

    того, що вона буде білого

    кольору?

А. ; Б. ;В. ; Г.

2. Розв’яжіть нерівність:

    .

       А.    ; 

       Б.   ; 

       В.   ;   

       Г.    .

 

2. Розв’яжіть нерівність:   

.

       А.    ;    

       Б.   ;              

       В.   ;       

       Г.    .

2.  Розв’яжіть нерівність:

      .

       А.    ;  

       Б.   ; 

       В.   ;   

       Г.  

3. Чому дорівнює об'єм

    циліндра, якщо його осьовим

    перерізом є квадрат зі

    стороною 4см?

http://fizma.net/df/geo/tila/img/img19.gif

А. 2 см3;

Б. 4 см3;

В. 8 см3;   

Г. 16 см3.

3. Чому дорівнює об'єм

    циліндра, якщо його осьовим

    перерізом є квадрат зі

    стороною 6см?

http://fizma.net/df/geo/tila/img/img19.gif

А. 12 см3;

Б. 54 см3;

В. 36 см3;   

Г. 18 см3.

 

3. Чому дорівнює об'єм

    циліндра, якщо його

    осьовим перерізом є

    квадрат зі стороною 10см?

http://fizma.net/df/geo/tila/img/img19.gif

А. 250 см3;

Б. 50 см3;

В. 100 см3;   

Г. 15 см3.

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть інтеграл: 

    

   Відповідь 12

1. Обчисліть інтеграл: 

    

   Відповідь 48

 

1. Обчисліть інтеграл:  

     .

Відповідь 18

2.  Установіть відповідність між  виразом  (1 - 4) та  його числовим значенням (А –Д).

 

1

sin ()

2

cos ()

3

tg ()

4

сtg ()

А

Б

  

В

Г

Д

 

1- А, 2- В, 3-Д, 4-Г

 

2.  Установіть відповідність між  виразом  (1 - 4) та  його числовим значенням (А –Д).

 

1

sin ()

2

cos ()

3

tg ()

4

сtg ()

А

Б

  

В

Г

Д

 

        1- А, 2- Б, 3-Д, 4-Г

 

2. Установіть відповідність між  виразом  (1 - 4) та  його числовим значенням (А –Д).

 

1

sin ()

2

cos ()

3

tg ()

4

сtg ()

А

Б

 

В

Г

Д

 

         1- В, 2- А, 3-Г, 4-Д

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Наведіть повне розв’язання задачі:  Яку найменшу кількість метрів паркану потрібно замовити, щоб загородити ділянку землі площею 25 а?

 

 

Відповідь 200 м

Наведіть повне розв’язання задачі: Знайдіть довжини      (у м) сторін прямокутної  ділянки землі площею 36 а, щоб для її  огорожі знадобилось

 якнайменше паркану ?

 

       Відповідь 60 м і 60 м.

 

Наведіть повне розв’язання задачі:    Знайдіть довжини    (у м) сторін прямокутної ділянки землі площею 16 а, щоб для її огорожі знадобилось якнайменше паркану ?

 

       Відповідь 40 м і 40 м.

 

 

 

Завдання № 2

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Яка з наведених рівностей

    неправильна?

   А.     = 90 0

   Б.     = 45 0

   В.      = 270 0

   Г.      = 60 0

 1. Яка з наведених рівностей

      неправильна?

   А.     = 90 0

   Б.     = 45 0

   В.      = 30 0

   Г.    2  = 360 0

 

1. Яка з наведених рівностей

    неправильна?

   А.     = 90 0

   Б.     = 45 0

   В.      = 30 0

   Г.    2  = 180 0

2. Якій із координатних осей

   належить точка A(0;-2;0)?

        А.   Жодній .

        Б.    Oy

        В.    Ox

        Г.    Oz

2. Якій із координатних осей 

    належить точка  B(3;0;0)?

        А.   Жодній .

        Б.    Oy

        В.    Ox

        Г.    Oz

2. Якій із координатних осей

 належить точка C(0;0;-5)?

        А.   Жодній .

        Б.    Oy

        В.    Ox

        Г.    Oz

3.  Знайдіть критичні точки

     функції f (x), якщо відомо,

     що  f '(х) = x2– 9 х.

       А.    3

        Б.     4,5

        В.     0 ; 9

        Г.  – 3 ; 3

3.  Знайдіть критичні точки

     функції f (x), якщо відомо,

     що  f '(х) = x2 – х.

       А.    1

        Б.     0 ; 1

        В.     0,5

        Г.  – 1 ; 1

3.  Знайдіть критичні точки

     функції f (x), якщо відомо,

     що  f '(х) = x2– 5 х.

       А.    5

        Б.     3,5

        В.     0 ; 5

        Г.  – 5 ; 5

4. Як знайти число, 60 %

    якого дорівнюють 360?

А.  360*60;      Б.   ;            В. ;   Г.  .

 

 

 4.  Як встановити, скільки

      відсотків становить число

      9 від 96?

 

А.  ;    Б.   ;            В. ;   Г. .

 

4.  Як знайти 52 %  від числа

      960?

  А.  960: 52;    Б.  ;            В. ;     Г.  960*52

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.Знайдіть корені рівняння

     6 cos х = 5.

   А. arccos + k , k Z

   Б.   arccos + 2k , k Z

   В. (-1)k arccos + k , k Z

   Г.  Розв’язків немає.

1.Знайдіть корені рівняння

     cos х = .

   А.       +2k, k Z

   Б.   (-1)k + 2k , k Z

   В.    + k , k Z

   Г.    + 2k , k Z

1.Знайдіть корені рівняння

       sin х = .

   А.   (-1)k + 2k , k Z

   Б.   + 2k , k Z

   В.    + k , k Z

   Г.    (-1)k + k , k Z

2. Зі  слова «математика»

    навмання вибирають одну

   літеру. Яка ймовірність

  того, що виберуть літеру «а»?

А.; Б. ; В. ; Г.

 

 

  1. Зі  слова «геометрія»

     навмання вибирають одну

    літеру. Яка ймовірність того, що виберуть літеру «е»?

А. ;  Б. ; В.  ; Г.

 

  1.  Зі  слова «трикутник»

    навмання вибирають

    одну літеру. Яка ймовір-

    ність того, що виберуть

   літеру «и»?

 А. ; Б. ; В.; Г.

 

3. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює  6 см, а бічне ребро призми

8 см.

http://img-fotki.yandex.ru/get/5311/136164467.1/0_ca451_8f5ca379_M.png

А. 288 см3  ; 

Б.  48см3;  

В.  92см3;   

Г.  192 см3

 

 

3. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює  3см, а бічне ребро призми

4 см.

http://img-fotki.yandex.ru/get/5311/136164467.1/0_ca451_8f5ca379_M.png

А. 27 см3  ; 

Б.  9см3;  

В.  36см3;   

Г.  64 см3

 

 

3. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює  5 см, а бічне ребро призми

6 см.

http://img-fotki.yandex.ru/get/5311/136164467.1/0_ca451_8f5ca379_M.png

А. 30 см3  ; 

Б. 16см3;  

В.  25см3;   

Г.  150 см3

 

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть інтеграл: 

            

      Відповідь

1. Обчисліть інтеграл: 

           

 

     Відповідь 15

 

1. Обчисліть інтеграл:  

         

 

    Відповідь 7

2. Установіть відповідність 

    між нерівностями (1 - 4) та

    множинами їх розв’язків

    (А – Д).

 

1

5х  > 30

2

- 5х  > 30

3

5х  < 30

4

- 5х  < 30

А

Б

В

Г

Д

      1- Д, 2- А, 3-Б, 4-В

2. Установіть відповідність 

    між нерівностями (1 - 4) та

    множинами їх розв’язків

    (А – Д).

 

1

4х  > 20

2

- 4х  > 20

3

4х  < 20

4

- 4х  < 20

А

Б

В

Г

Д

  

 

          1- Б, 2- А, 3-Д, 4-В

2. Установіть відповідність 

    між нерівностями (1 - 4) та

    множинами їх розв’язків

    (А – Д).

 

1

8х  > 32

2

- 8х  > 32

3

8х  < 32

4

- 8х  < 32

А

Б

В

Г

Д

    1- Д, 2- В, 3-Б, 4-А

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

  1. Наведіть повне розв’язання задачі: З точки А до площини проведено дві похилі АВ і АС. Знайдіть довжини похилих, якщо  одна з них на 26 см більша від другої, а проекції похилих дорівнюють 12 см і 40 см.

 

Відповідь 15, 41

1.  Наведіть повне розв’яза-

     ння задачі: З точки А до

     площини проведено дві

     похилі АВ і АС . Знайдіть

     довжини похилих, якщо

     похилі відносяться як 1: 2,

     а проекції похилих дорівню-

     ють 1см і 7 см.

 

      Відповідь 4, 8

 

  1. Наведіть повне розв’яза-

    ння задачі:   З точки А до

    площини проведено дві

   похилі АВ і АС .Знайдіть

   довжини похилих, якщо 

   одна з них на 10 см менша

   від другої, а проекції похи-

   лих дорівнюють 18 см і

   32 см.

     Відповідь  30,40

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Завдання № 3

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Яка з наведених

    нерівностей правильна?

   А.  sin 50 0 < 0

   Б.   cos 225 0 < 0

   В.    tg 60 0 < 0

   Г.    ctg 335 0 > 0

 

 1.  Яка з наведених

      нерівностей правильна?

   А.  sin 80 0 > 0

   Б.   cos 130 0 > 0

   В.    tg 210 0 < 0

   Г.    ctg 310 0 > 0

 

1.  Яка з наведених

     нерівностей правильна?

   А.  sin 100 0 > 0

   Б.   cos 130 0 > 0

   В.   tg 20 0 < 0

   Г.   ctg 250 0 > 0

2. Спростіть  вираз (а4)12 : а8

А. а2; Б. а6; В. а40 ;  Г. а8

2. Спростіть  вираз (а3)10: а12

А. а5; Б. а18; В. а30 ;  Г. а6

2. Спростіть  вираз (а5)8: а17

А. а23; Б. а6; В. а30 ;  Г. а57 

3. Знайдіть значення виразу 

         .

 

   А.    0,4

   Б.    0,2

   В.    0,0002

   Г.    0,0004

 

3. Знайдіть значення виразу 

               .

   А.    0,00002

   Б.    0,2

   В.    0,5

   Г.    0,00005

3. Знайдіть значення виразу

            .

 

   А.    0,009

   Б.   

   В.    0,003

   Г.    0,3

4. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

    наведених прямих перпенди-

    кулярна до площини ACC1?

 

        А.   DD1     

        Б.    B1D1

        В.    BD1

        Г.    DC

 

 

4. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

   наведених прямих перпенди-

   кулярна до площини DCC1?

 

        А.   AA1     

        Б.   A1D1

        В.    D1B

        Г.    BC1

 

4.  На рисунку зображено куб

     ABCDA1B1C1D1. Яка з

     наведених площин перпен-

     дикулярна до прямої  AC?

 

        А.   A1B1C1     

        Б.   ACC1

        В.    BCC1

        Г.    BDD1

 

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть загальний вигляд

    первісних для   функції:

    f(x) = x10 – x8 + x + 13

А  

Б;  

В ;    Г

 

1. Знайдіть загальний

    вигляд первісних для 

   функції:  

 f(x) = x12 – x5 + x + 4

А      Б ;  

В   Г

 

1. Знайдіть загальний вигляд

    первісних для   функції:

    f(x) = x24 + x16 - x -10

А      Б;  

В ;    Г

2. При якому значенні  n

    вектори  (3;-5;n) і

 (n;1;2) перпендикулярні?

 

       А.     1

       Б.   - 1

       В.   - 5

       Г.      3

 

2. При якому значенні  n

   вектори  (3;-3;n) і (n;5;2) перпендикулярні?

 

       А.     5

       Б.   - 3

       В.   - 5

       Г.      3

 

2. При якому значенні  n

   вектори  (8;n;6) і

(4;2;3) перпендикулярні?

 

       А.     -5

       Б.   - 25

       В.      5

       Г.     25

 

3. Обчисліть об’єм конуса, висота якого 9 см, а радіус основи 5 см.

А. 75 см3;  

Б. 45 см3; 

В. 25 см3;    

Г. 81 см3.

 

3. Обчисліть об’єм конуса, висота якого 4 см, а радіус основи 3 см.

А. 36 см3;  

Б. 4 см3; 

В. 12 см3;    

Г. 12 см3.

 

3. Обчисліть об’єм конуса, висота якого 8 см, а радіус основи 6 см.

А. 36 см3;  

Б.  96 см3; 

В. 48 см3;    

Г. 64 см3.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Розв’яжіть нерівність:

         

 Відповідь

 

  1. Розв’яжіть нерівність:  

          

 Відповідь

 

  1. Розв’яжіть нерівність: 

          

 Відповідь

 

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

    його розв’язками ( А –Д).

 

1

sin 2х = 0

2

cos 2х = 1

3

tg = 0

4

сtg = 1

А

+k , kZ

Б

2k , kZ

В

k , kZ

Г

+2k ,kZ

Д

,kZ

           1- Д, 2- В, 3-Б, 4-Г

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

    його розв’язками ( А –Д).

 

1

sin х = 0

2

cos х = - 1

3

tg х = 1

4

сtg х = 0

А

+k , kZ

Б

+2k, kZ

В

k , kZ

Г

+k ,kZ

Д

+2k, kZ

 

         1- В, 2- Д, 3-А, 4-Г

 

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

   його розв’язками ( А –Д).

 

1

sin х = 1

2

cos х = 0

3

tg х = 0

4

сtg х = - 1

А

+k, kZ

Б

+2k, kZ

В

k , kZ

Г

+k ,kZ

Д

+2k, kZ

 

1- Б, 2- Г, 3-В, 4-А

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Наведіть повне розв’язання

    задачі: Функцію задано формулою f (x) = – 16 х.

    1) Знайдіть критичні точки функції f (x).

    2)  Знайдіть найбільше і найменше значення функції

f (x) на відрізку [-3; 1]

     Відповідь 1) -2,2.

 2)max f(x)= f(-2)= ,

 min f(x)= f(1)=

1.  Наведіть повне розв’яза-

     ння задачі:  Функцію

     задано формулою

     f (x) = – 8 х.

    1) Знайдіть критичні точки функції f (x).

    2)  Знайдіть найбільше і найменше значення функції

f (x) на відрізку [0; 3]

     Відповідь 1) -2,2.

 2)max f(x)= f(0)= 0,

 min f(x)= f(2)= .

 

1.  Наведіть повне розв’яза-

      ння задачі:  Функцію

      задано формулою

      f (x) =  х – х3.

    1) Знайдіть критичні точки функції f (x).

    2)  Знайдіть найбільше і найменше значення функції f (x) на відрізку [0; 1]

     Відповідь 1) -, .

2) max f(x)= f ()= ,

 min f(x)= f(1)= .

 

 

 

 

Завдання № 4

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.  Яка з наведених фігур

      може бути лінією перетину

      двох площин?

 

        А.   Три точки .

        Б.    Відрізок.

        В.    Пряма.

        Г.    Будь-яка лінія. 

 

  1. Через яку з наведених

фігур можна провести

безліч площин?

 

  А. Паралельні прямі .

  Б.  Мимобіжні прямі.

  В. Прямі, що перетинаються.

  Г.    Пряму і точку на ній.

 

1.  Точка M не лежить у

      площині паралелограма

     ABCD. Яке взаємне

     розміщення прямих MC і

     AB?

 А.Перетинаються .

 Б. Мимобіжні.

 В. Перетинаються або мимо-

      біжні.

 Г.  Паралельні

 

2. Знайдіть найбільший кут

    трикутника, якщо градусні

    міри всіх кутів відносяться

    як 3:4:5.

   А. 600;              Б.  450;

   В. 750 ;             Г. 1050 .

2.  Знайдіть найменший кут

     трикутника, якщо градусні

     міри всіх кутів відносяться

     як 2:3:5.

    А. 540;           Б.  360; 

    В. 900 ;          Г. 180 .

2.  Знайдіть найбільший кут

     трикутника, якщо градусні

     міри всіх кутів відносяться

     як 4:6:8.

    А.  600;        Б.  400; 

    В. 1000 ;       Г. 800 .

 

3. Обчислити:   

      А. 200;       Б.  8000;

      В. 1600 ;     Г.  400.

3. Обчислити: 

  * - .

        А.  1;       Б.  2;

        В.  3 ;      Г.  4.

3. Спростити вираз:

  10  + +

   А. 17;   Б.  39;

   В. 19 ;  Г   24.

4.  Скількома способами

     можна з 30 учнів вибрати

    трьох чергових?

    А. ;      Б. 30*3;

    В. ;       Г.

4.  Скількома способами

      можна з 18 учнів вибрати

      трьох делегатів на

      конференцію?

    А. ;   Б  ; 

    В.;      Г. 18*3.

4.  Скількома способами

     можна з 25 учнів вибрати

     трьох чергових?

    А. ;   Б.  25*3; 

    В.  ;   Г. .

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть похідну функції  (х6 + 3x2 – x + 3)' = …

   А.   6x5 + 6x

   Б.   + x3 + 3x

   В.    6x5 + 6x - 1

 

   Г.    6x5 + 6x + 3

 

1. Знайдіть похідну функції  (х10 + 4x2 +7x - 2)'= …

   А.   10x9 + 8x

   Б. +x3 - 2x

   В.    10x5 + 8x - 2

 

   Г.    10x9 + 8x + 7

 

1. Знайдіть похідну функції  (х7 + 5x2 – 10x + 4)'=…

 А.   7x6 + 10x - 10

 Б. +x3 – 5x2 + 4x

 В.   7x6 + 10x + 4

 

 Г.   7x6 + 10x

2. Знайти множину розв’язків

    нерівності 

    log3(x-4) log38

 

    А. ;  Б. ;

    В. ;      Г.

 

 

2.   Знайти множину

      розв’язків  нерівності

              log5x < 2

 

 

  А. ;  Б. ;

  В. ;        Г.

 

 

2.   Знайти множину

      розв’язків  нерівності

  log0,1(2x-5) > log0,1x

 

   А. ;   Б. ;

   В. ;     Г.

 

 

3. Сторона основи правиль-

      ної трикутної піраміди

      дорівнює 6 см, а бічне

      ребро – 5 см. Знайдіть

      бічну поверхню піраміди.

   А.  12см2.

   Б.  72см2.

   В.  36см2.

   Г.  45см2.

 

  1. Сторона основи правиль-

       ної трикутної піраміди

       дорівнює 18 см, а бічне

       ребро – 15 см. Знайдіть

       бічну поверхню піраміди.

 

   А.  108см2.

   Б.  36см2.

   В.  225см2.

   Г.  30см2.

 

3.  Сторона основи правиль-

     ної трикутної піраміди

     дорівнює 8 см, а бічне

     ребро – 10 см. Знайдіть

     бічну поверхню піраміди.

 

   А.  18см2.

   Б.  24см2.

   В.  28см2.

   Г.  48см2.

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Діагоналі паралелограма ABCD перетинаються в точці  O(-3;1;-2). Знайдіть координати  вершини A , якщо 

     C(-1;3;4).

 

      Відповідь  A(-5;-1;-8)

 

  1. Точка M є серединою

      відрізка  PC. Знайдіть

      координати точки P,

      якщо M(-1;3;2),

      C(2;-3;0).      

 

 

 Відповідь  P(-4;9;4)

1. Точка B є серединою

    відрізка  AC. Знайдіть

    координати точки C,

    якщо A(1;2;3), B(3;2;1).

 

 

 Відповідь   C(5;2;-1)

2. Установіть відповідність

    між  виразами (1 - 4) та

    тотожно рівними їм

    виразами ( А –Д).

 

1

(2a - 3)*(3a + 2)

2

(2a - 3)2

3

(3 - 2a)*(3 + 2a)

4

(3 + 2a)2

А

9 + 12a + 4a2

Б

6a2- 5a - 6

В

4a2- 6a + 9

Г

9 – 12a + 4a2

Д

9 - 4a2

1- Б, 2- Г, 3-Д, 4-А

 

  1. До кожного виразу (1 - 4) 

      доберіть тотожно рівний

      йому вираз ( А –Д).

 

1

(a - 8)*(a + 8)

2

(a - 8)2

3

(a - 4)*(a2+4a+16)

4

(a - 4)*(a - 16)

А

a2- 16a + 64

Б

a2- 64

В

a2- 20a + 64

Г

a3 + 64

Д

a3 - 64

 

1- Б, 2-А , 3-Д, 4-В

 

  1. До кожного виразу (1 - 4)

      доберіть тотожно рівний

      йому вираз ( А –Д).

 

1

(a - 5)*(a +5)

2

(a - 5)2

3

(5 + 2a)2

4

(2a - 5)*(2a + 5)

А

a2- 10a + 25

Б

a2- 25

В

25 + 20a + 4 a2

Г

4a2 + 25

Д

4a2 - 25

 

1- Б, 2-А , 3-В, 4-Д

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

  1.      Розв’яжіть  рівняння  

2cos 3 х  - = 0.

Відповідь  + , k Z  

  1. Розв’яжіть  рівняння  

2 sin 5 х  - = 0.

 Відповідь (-1)k + ,kZ

  1.    Розв’яжіть  рівняння  

2 sin 5 х  - = 0.

Відповідь (-1)k + , kZ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Завдання № 5

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

  1. Вкажіть графік якої функції

    зображено на рисунку.

 

 А. f (x) = sin х  Б. f (x) = 

 В. f (x) = tg x    Г. f (x) = x + 1

1.Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = Б. f (x) = sin х   

 В. f (x) = cos х  Г. f (x) =   

1. Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = tg x  

 Б. f (x) = cos х    

 В.  f (x) = 

 Г.  f (x) = sin х 

2. Через яку з наведених фігур

    можна провести площину і до

    того ж тільки одну?

        А.   Три точки .

        Б.    Точку і пряму.

        В.    Дві будь-які прямі.

        Г.    Дві прямі, що мають

                спільну точку.

2.Відомо, що площини і мають одну спільну точку.

  Скільки ще спільних точок

  мають ці  площини  ?

        А.   Жодної .

        Б.    Безліч.

        В.    Тільки дві.

        Г.    Тільки три. 

2. Яка з наведених фігур не

    може бути паралельною

    проекцією прямокутника?

 

        А.    Паралелограм .

        Б.    Трапеція.

        В.    Прямокутник.

        Г.    Квадрат. 

3.  Чому дорівнює  швидкість змінювання функції 

f (t) = t3+3t2 у точці  t = 4 ?

       А.     48

       Б.   120

       В.      72

       Г.     36

3.   Матеріальна точка

     рухається вздовж осі Ох за

     законом х = х(t). У якому

     з наведених    випадків

     швидкість цієї матеріальної

    точки є сталою?

   А.  х(t) = t2 – 3t ; 

   Б.  х(t) = t3 – 3t2

   В.  х(t) = 3t – t2

   Г.  х(t) = 3t – 32

3.  Чому дорівнює  швидкість

     змінювання функції

 f(t)= t3 – 4t2 у точці  t = 5 ?

       А.     35

       Б.    115

       В.      20

       Г.     70

4.  Значення якого виразу є

     додатним числом ?

А. sin 120 0   Б. cos 210 0

В. tg 100 0     Г. ctg 320 0

4.  Значення якого виразу є

     додатним числом ?

А.  sin 190 0   Б.   cos 300 0

В.  tg  290 0    Г.   ctg 100 0  

 

4.  Значення якого виразу є

     додатним числом ?

А.  sin 300 0    Б.  cos 95 0

 В.  tg 200 0     Г.  ctg 170 0

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.Один з гострих кутів прямо- 

    кутного трикутника на 180

    більший від іншого. Знайдіть

    більший  з цих кутів.

А.660;  Б.540;  В.360; Г.480 .

  1. Один з гострих кутів прямо-

    кутного трикутника у 5 разів

   більший від іншого. Знайдіть

   найменший  з цих кутів.

А.900;  Б.450;  В.150 ;  Г.750.

1. Один з гострих кутів прямо-

    кутного трикутника на 100

    більший від іншого. Знайдіть

    менший з цих кутів.

А. 400;  Б.500;  В.900; Г.100 .

2.   Розв’яжіть нерівність

              5х > 5

А. ;       Б. ;         В.   ;      Г.

2.   Розв’яжіть нерівність

     0,7х < 1

А. ;    Б. ;         В.   ;      Г.

2.   Розв’яжіть нерівність

          2х < 32

А. ;   Б. ;         В.  ;   Г.

3. Площа великого круга кулі дорівнює 4см2. Знайдіть об’єм кулі. 

 

 А.  64см3.

 Б.  16см3.

 В.  32см3.

 Г.  см3

3. Діаметр кулі дорівнює 6 см. 

    Знайдіть площу поверхні

    кулі. 

 

   А.  54см2.

   Б.  36см2.

   В.  72см2.   

   Г.  18см2

 3. Діаметр кулі дорівнює

    10 см.  Знайдіть площу

    поверхні кулі. 

 

   А.  50см2.

   Б.  40см2.

   В.  25см2.

   Г.  100см2

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть: 

   * *

Відповідь 4   

1. Обчисліть:

      *

Відповідь 2   

1. Обчисліть:  

      *

Відповідь 3

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

40 %

Б

20 %

В

80 %

Г

12,5 %

Д

25 %

          1- Д, 2- А, 3-Г, 4-В

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

60 %

Б

50 %

В

80 %

Г

62,5 %

Д

20 %

 

          1- Б, 2- Д, Г, 4-А

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

40 %

Б

20 %

В

37,5 %

Г

62,5 %

Д

75 %

     1- Г, 2- Д, 3-В, 4-А

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Розв’яжіть  рівняння             = x - 1.

Відповідь5

1.  Розв’яжіть  рівняння      = 4 - x.

Відповідь 2

 1. Розв’яжіть  рівняння      =  x.

Відповідь 4

 

 

 

 

 

 

Завдання № 6

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

  1. Вкажіть графік якої функції

    зображено на рисунку.

 А. f (x) = ;  Б. f (x) = -  x 2;

 В. f (x) = tg x;  Г. f (x) = x + 2

1.Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = x 2;  Б. f (x) = cos х; 

 В. f (x) = - (x – 1)2;

 Г. f (x) = - x 2  

1. Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = x;    Б. f (x) = x + 1;

 В.  f (x) = x + 2;

 Г.  f (x) =  x - 1

2. Спростіть вираз

      5- +   

А. 6;  Б.20 ; В.2;  Г. 52.

2. Спростіть вираз

      6 - +

А. 25;  Б. 7; В.70;  Г. 5

2. Спростіть вираз

      7 - +

А.7;  Б.36 ; В. 5;  Г. 53

3. На рисунку зображено куб ABCDA1B1C1D1. Перерізом куба площиною, що проходить через точки A, C, C1, є…                                                   

 А.  Прямокутний

       трикутник.

 Б.  Прямокутник.

 В.  Ромб.

 Г.  Трапеція.  

 

3. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

  наведених прямих паралельна

   площині (AA1B1)?                                                                         

   А.  BC.

   Б.  BD.

   В.  CB1.  

   Г.  C1D.

 

3.  На рисунку зображено прямокутний паралелепіпед ABCDA1B1C1D1. Яка з наведених прямих паралельна площині (ABC)?                                                                         

   А.  DD1.

   Б.  B1D.

   В.  A1C1.

   Г.  C1D.

4.  Обчисліть інтеграл:

         

А. ;  Б. ; В. ;  Г. 2.

4.  Обчисліть інтеграл: 

            

А. 19;  Б. 21;   В.;  Г. 20.

4.  Обчисліть інтеграл:

          

А.; Б. ;  В. ;  Г. 1.

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Катет прямокутного трику-

     тника дорівнює 12 см, а

     медіана, проведена до іншого

     катета, - 13 см.  Знайдіть

     гіпотенузу трикутника.

А   2см;      Б.  5см;             В.  25см ;            Г. 22см.

1.  Катет прямокутного трику-

     тника дорівнює 12 см, а

     медіана, що  проведена до

     нього, дорівнює –  8 см.

     Знайдіть інший катет

     трикутника.

 А.  4см;     Б. 2см;

 В.  8см ;           Г. 8см.

1.  Катет прямокутного трику-

     тника дорівнює 16 см, а

     медіана, що  проведена до

     нього, дорівнює –  2см.

     Знайдіть інший катет

     трикутника.

 А. см;        Б.  8см;

 В   12см ;           Г.  20см.

2.   Розв’яжіть рівняння

       log3(7 - x) = 2

 А. 0;    Б.16 ;   В.7 ;  Г. - 2

2.   Розв’яжіть рівняння

       lg (5х - 15) = 1

 А. 5;    Б.10 ;   В.15 ;  Г. 1

2.   Розв’яжіть рівняння

       log2(3х + 1) = 4

 А. 3;    Б.10 ;   В.5 ;  Г. 1

3. Діаметр основи конуса

    AB=8 см, а його висота

   SO=3см.Знайдіть твірну

    конуса SB.

   А.  см

   Б.  10см.

   В.  5см.

   Г.  2 см .

3.   Діаметр основи конуса

     AB=16 см, а його висота 

    SO=6см.Знайдіть твірну

     конуса SB.  

   А.  см

   Б.  10см.

   В.  5см.

   Г.  12 см .

 

 3.   Діаметр основи конуса

      AB=24 см, а його висота

     SO=9см.Знайдіть твірну

      конуса SB.

  А.  см

  Б.  33см.

  В.  5см.

  Г.  15 см .

 

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть:     

  Відповідь    

1. Обчисліть:    

 

Відповідь 102   

  1.    Обчисліть: 

 

Відповідь 16

2. Установіть відповідність

    між функцією (1 - 4) та  її 

    областю значень ( А –Д).

1

y = x

 

2

y = x 9

3

y = x -3

4

y = x -4

А

Б

В

Г

Д

1- Б, 2- Г, 3-Д, 4-А

2. Установіть відповідність

    між функцією (1 - 4) та  її 

    областю визначення ( А –Д).

1

y = x 8

2

y =  x

3

y = x -5

4

y =  x

А

Б

В

Г

Д

 

1- Г, 2- А, 3-Д, 4-Б

 

2. Установіть відповідність

     між функцією (1 - 4) та  її 

    областю визначення ( А –Д).

1

y = x - 4

2

y = x

3

y = x 9

4

y =  x

А

Б

В

Г

Д

 

1- В, 2- А, 3-Б, 4-Д

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Відомо, що sin =   і  <<. Знайдіть cos .

Відповідь

1.  Відомо, що cos =   і  <<. Знайдіть sin.

Відповідь

 1.  Відомо, що cos =   і  <<.Знайдіть sin.

Відповідь

 

 

 

Завдання № 7

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Обчислити:

1,521 : 0,3 – 1,9 * 0,3   

А.0; Б. – 0,063; В) 4,5 ; Г – 0,63

 

1. Обчислити:

- 4,8 : (- 2,6 + 3,4) + 0,8   

А - 7,2;  Б – 5,2 ;  В 5,2;  Г  6,8

 

1.  Обчислити:

- 144:(42 – 46) – 12* (-3)   

А  72;   Б 74 ;  В - 71 ;   Г  - 70

 

2. Чому дорівнює  кутовий коефіцієнт дотичної до графіка  функції  f (x) = 2х - x3

    у точці  х0 = 0 ?

  А.  – 2;  Б. – 1;  В. 0;  Г.  2

 

2.  Чому дорівнює  кутовий коефіцієнт дотичної до графіка  функції  f (x) =  x3 - 2х

      у точці  х0 = 0 ?

   А.  – 2;  Б. – 1;   В. 0;   Г. 1

2.  Знайдіть кутовий коефіцієнт

    дотичної до графіка  функції

     f (x) = 1,5 х2 - 5 у точці

      х0 = 1 ?

  А.  2;   Б. – 1;  В. -2;   Г.  3

3. Середня лінія трапеції

    MN = 12 см, а більша основа

   AD = 14 см. Знайдіть меншу

   основу BC.

А. 2см;

Б. 10см;

В. 26см;

Г. 14см.

3. Середня лінія трапеції

MN = 10 см, а менша основа  BC = 6 см .  Знайдіть більшу основу AD.

 А. 4см;

 Б. 16м;

 В. 12см;

 Г.  14см.   

 

3. Знайдіть cередню лінію

    трапеції MN, якщо менша 

    основа  BC = 10 см , а більша

    основа AD = 20 см.  

А. 10см; 

Б.  30см;

В. 15см ;

Г.  5см.     

 

4.  Укажіть правильну  нерів-

     ність, якщо а = sin 1200,

     b =  cos 1200.

    А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

 

4.  Укажіть правильну нерів-

     ність,  якщо а = sin 3000,

     b =  cos 3000.

   А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

 

4. Укажіть правильну нерів-

    ність,  якщо а = sin 300,

    b =  cos 300.

   А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

               

А.;        Б. ;

В. 2();   Г. 3().

 

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

              

А.;        Б. ;

В. 10();  Г. ().

 

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

              

А.;       Б. ;

В. 4();   Г. ().

 

2.   Знайдіть загальний вигляд

      первісної для функції 

       .

 А.   ; 

 Б.   ;            

 В.    ;  

 Г.   .

 

2.   Знайдіть загальний вигляд

      первісної для функції 

         .

 А.   ;

 Б.   ;  

 В.  ; 

 Г   .

2.   Знайдіть загальний вигляд

      первісної для функції 

         .

А.  ;               Б.  ; 

В.  ;            Г.  .

3. Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 2см, 3см і 6 см.

  А.  49см.

  Б.  36см.

  В.  11см.

  Г.  7см.

 

3.  Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 6см, 8см і 10 см.

А. 10см

Б. 24см.

В. 18см.

Г. 14см .

 3. Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 4см, 6см і 8 см.

А. 10см

Б. 2см

В. 18см.

Г. 18см

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1.  Розв’яжіть рівняння

 

            8 sin х = 7.

 

   Відповідь:

  (-1)k arcsin + k , k Z

  1. Розв’яжіть рівняння

            sin 3 х = .

Відповідь:

      (-1)k + , k Z

 1.  Розв’яжіть рівняння

       cos 2х = .

Відповідь:

     + k , k Z

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

1

2

3

4*4! – 42

4

3! + 4!

А

30

Б

40

В

60

Г

80

Д

90

 

        1- Д, 2- В, 3-Г, 4-А

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

1

2

3

3*3! – 32

4

2! + 4!

А

30

Б

40

В

26

Г

56

Д

9

 

           1- Г, 2- Б, 3-Д, 4-В

 

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

1

2

3

2*5! – 52

4

3! + 2!

А

215

Б

42

В

60

Г

8

Д

90

 

          1- Б, 2- Д, 3-А, 4-Г

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Наведіть повне розв’язання задачі: Кулю, радіус якої 5 см, перетнуто площиною, що розміщена на відстані 3 см від центра. Знайдіть площу перерізу.

 

Відповідь:   16см2

1. Наведіть повне розв’язання

   задачі:Кулю, радіус якої 15 см,

   перетнуто площиною, що

   розміщена на відстані 9 см від

   центра. Знайдіть площу

   перерізу.

 

 Відповідь:   144см2.

 

1. Наведіть повне розв’язання

   задачі: Кулю, радіус якої 10 см,

   перетнуто площиною, що

   розміщена на відстані 6 см від

   центра. Знайдіть площу

   перерізу.

          

    Відповідь:   64см2.

 

 

 

 

Завдання № 8

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

  1. Розгортка  якого  тіла

    зображена на рисунку.

         

 А. Піраміда;    Б. Призма;

 В. Конус         Г.  Куб

  1.   Розгортка  якого  тіла

      зображена на рисунку.

         

 А. Піраміда;    Б. Призма;

 В. Конус         Г.  Куб

 

  1.    Розгортка  якого  тіла

       зображена на рисунку.

            

 А. Піраміда;    Б. Призма;

 В. Конус         Г.  Куб

2. Яке з наведених чисел не

  належить області  визначення

 функції  f (x) = ?

А. 2;   Б.  – 5;   В.  5;     Г.  7

 

2. Яке з наведених чисел не

  належить області  визначення

  функції  f (x) = ?

 А.  1;  Б. 0;    В. – 3;   Г.  – 7 

2.  Яке з наведених чисел не

   належить області  визначення

   функції  f (x) = ?

 А.  – 2;   Б. – 4;   В. 0;    Г. 1.

3. Знайдіть радіус кола, якщо

    довжина кола дорівнює

    24см.

А. 4см;         Б.  48см;             В. 12см ;           Г.  24см.     

 

3. Знайдіть радіус кола, якщо

    довжина кола дорівнює

    32см.

А. 16см;       Б.  16см;             В. 32см ;           Г.  64см.     

 

3. Знайдіть радіус кола, якщо

    довжина кола дорівнює

    46см.

  А. 23см;     Б.  92см; 

  В. 46см ;         Г.  23см.     

 

4.  Обчисліть інтеграл:  

     А.1;  Б. ;  В. ;  Г.0 .    

 

4. Обчисліть інтеграл: 

    А. ;  Б.1;  В. ;  Г.0

4. Обчисліть інтеграл: 

     А. 4;  Б. ;  В. ;  Г.0 .

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Медіаною сукупності

   даних:  2; 7; 9; 11; 15

   є число

  А.  7;  Б.10;  В. 11;  Г. 9

1. Медіаною сукупності

    даних:  5; 7; 9; 11; 13; 15;17

    є число

  А.  12;  Б.9;  В. 11;  Г. 10  

1. Дано вибірку : 3,6;  3,6;  3,5;

    3,1;  3,6;  3,5;  3,4;  3,7. 

   Знайдіть моду цієї вибірки.

 А. 3,6;  Б. 3,7;   В. 3,5;  Г. 3,4.

 

2.  Знайдіть критичні точки 

  функції 

  А. 0;             Б.  - 3 і 1;

  В.  - 1 і 3 ;    Г.    1 і 3.    

 

2.   Знайдіть критичну точку

      функції  

          

  А. - 1;         Б.   1;

  В.   4 ;         Г.   2.

 

2.   Знайдіть критичні точки

    функції  

  А. 0;           Б.  - 3 і 3;

  В. 0 і 3 ;     Г.    0 і 9.

 

3. Діагональ грані  куба  AC = 4см. Знайдіть об’єм куба.                   

   А.  16см3.

   Б.  64см3.

   В.  4см3.

   Г.  48см3.

 

 

3. Діагональ грані  куба  AC = 5см . Знайдіть об’єм куба.                   

   А.  125см3.

   Б.  50см3.

   В.  10см3.

   Г.  20см3.

 

3. Діагональ грані  куба  AC = 6см . Знайдіть об’єм куба.                   

   А.  12см3.

   Б.  72см3.

   В.  24см3.

   Г.  216см3.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Розв’яжіть нерівність:

         

 Відповідь  

 

  1. Розв’яжіть нерівність:  

          

 Відповідь  

 

  1. Розв’яжіть нерівність: 

          

 Відповідь 

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

-+

2

+-

3

--

4

+-

А

2

Б

3

В

4

Г

5

Д

6

 

        1- Г, 2- А, 3-Б, 4-В

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

-+

2

-+

3

- -

4

-+

А

2

Б

8

В

4

Г

5

Д

12

 

           1- В, 2-Б , 3-А, 4-Д

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

+-

2

-+

3

-+

4

--

А

2

Б

3

В

Г

5

Д

7

 

           1-Д, 2- А, 3-Б, 4-В

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Знайдіть значення виразу 

 4 cos- sin (),

    якщо =

                      Відповідь 3

 

1. Знайдіть значення виразу 

     tg + sin (),

   якщо =

                     Відповідь

 

1. Знайдіть значення виразу 

      cos + ctg (),

     якщо =

                    Відповідь

 

 

Завдання № 9

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

  1.  Яку формулу використо-

    вують  для обчислення

    об’єму конуса?

Картинки по запросу рисунки по геометрии 10-11 класс

А. V = πR2H;     Б.V = πR2H; 

В.  V = abc ;      Г.  V =

  1. Яку формулу використо-

   вують  для обчислення

   об’єму  циліндра?

А. V = πR2H;     Б.V = πR2H; 

В.  V = abc ;      Г.  V =

  1.  Яку формулу використо-

    вують  для обчислення

    об’єму  кулі?

 

А. V =;     Б.V = πR2H; 

В.  V = abc ;      Г.V = πR2H

2.  Обчисліть:  

А. ;    Б. ;   В.  ;  Г. .

 

2.  Обчисліть:  

А. ;    Б. ;   В.  ;  Г. .

2.  Обчисліть:  

  А. ;    Б. ;   В.  ;  Г.

3. Дослідіть на парність  функцію   f (x) =  4x7 - 2х3

  А. непарна;         Б. парна;  

  В. ні парна, ні непарна;  

  Г. встановити неможливо 

3. Дослідіть на парність 

   функцію   f (x) =  x2 - 3х4

  А. непарна;         Б. парна;  

  В. ні парна, ні непарна;  

  Г. встановити неможливо 

3. Дослідіть на парність

    функцію   f (x) =  x3 + х6

   А. непарна;         Б. парна;  

   В. ні парна, ні непарна;  

   Г. встановити неможливо 

 

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

 

     А. 360; 

     Б.  180;

     В. 720 ;

     Г. 1080 .

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

  А. 690;

  Б.  110; 

  В. 420;

  Г. 1110

 

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

   А. 670; 

   Б. 230; 

   В. 900;

   Г. 15

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть похідну функції

f (x) = x3 + x2 – х + 5.

   А.   3x2 +  x – х + 5

   Б.   3x2 +  x – 1

   В.    3x2 +  x – 1

   Г.    3x2 +  2x2 – 1

 

1. Знайдіть похідну функції

f (x) = x4 + 3x3 + х – 2.

   А.   x3 + x2 + х

   Б.   4x3 +  x2 + х – 2

   В.    x3 +  9 x2 + 1

   Г.    x3 +  9 x2 + x

 

1. Знайдіть похідну функції

 f (x) =x5 + x3 + 4х – 2.

   А.   x4 + x2 + х

   Б.   x4 +  3x2 + 4

   В.    x4 +  3 x2 + х

   Г.    x4 +  3 x2 - 2

 

2.  Розв’яжіть рівняння: 

           log4(x+2) = 2

 

   А. 18;   Б.  14;   В.  0;    Г.  6.

2.   Розв’яжіть рівняння :

              log3(х-1)=3.

 

      А. 28;   Б. 26;     В. 10;   Г. 8.

 

  1. Розв’яжіть рівняння:

         log 2  (х+8) = log 2 10  

 

     А. 10;   Б.  8;   В.  2;    Г.  18.

 

3. Знайдіть повну поверхню

    циліндра з радіусом 5 см і

    висотою 15 см.

 

   А.  100см2.

   Б.  400см2.

   В.  200см2.

   Г.  150см2

 

3. Знайдіть повну поверхню

    циліндра з радіусом 3 см і

    висотою 10 см.

 

   А.  78см2.

   Б.  300см2.

   В.  250см2.

   Г.  30см2

 3. Знайти повну поверхню

     циліндра з радіусом 4 см і

     висотою 12 см.

   А.  16см2.

   Б.  32см2. 

   В.  268см2.

   Г.  128см2

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Знайдіть скалярний добуток

    векторів і  , якщо: 

  ,    

Відповідь  14                                                                      

 

1. Знайдіть скалярний добуток

    векторів і  , якщо:

   ,                                                                                 

         Відповідь  5                                                                  

 

1. Знайдіть скалярний добуток

    векторів і  , якщо: 

,                                                                                

        Відповідь  8                                                                    

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

2

3

4

А

Б

В

Г

Д

 

        1- В, 2- Г, 3-Д, 4-А

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

 

1

2

3

4

А

Б

 2

В

Г

Д

 

           1- Д, 2-Г , 3-Б, 4-А

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

 

1

2

3

4

А

1

Б

В

Г

Д

 

           1-А, 2- Д, 3-В, 4-Б

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Знайдіть значення виразу 

 +  +

          Відповідь 36                   

 

1. Знайдіть значення виразу 

++

         Відповідь 22

1. Знайдіть значення виразу     - +

 

         Відповідь 117

 

 

 

 

 

 

 

Завдання № 10

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.   Яка з наведених рівностей

      правильна?

А.;     Б. ; 

В.;   Г. .

1.   Яка з наведених рівностей

      правильна?

А.;       Б.; 

В. ;  Г..

 1.   Яка з наведених рівностей

      правильна?

 А. ;  Б.; 

 В ;    Г .

2.    Обчисліть:  

         

А. 100;   Б.  4;   В.  25;  Г.  2.

2.   Обчисліть: 

         log216 – lg1000   

А. 1;   Б.  2;   В.  - 1;  Г.  3.

 2.     Обчисліть:  

         log5125 + lg100

 А. 125;   Б.  25;   В.  5;  Г. 100.

 3.   Спростіть вираз: 

         .

   А. 1;  Б.  -1;  В. 0;  Г. 3.

3.   Спростіть вираз: 

.

    А.;       Б. ;

    В.  ;     Г. .       

 

 3.    Спростіть вираз: 

         .

    А. 1;    Б. 0;    В - 1;   Г.   3.

 4.  Знайдіть координати

середини відрізка АВ – точки К, якщо   А(3;2;9) і В(5;2;3).

 

 А.  К (4;2;6);     Б.  К (8; 4; 12);

В.  К (-1;0; 3);   Г.  К(-2; 0; 6).

4.    Знайдіть координати середини відрізка АВ – точки К, якщо А(10;3;8) і В(6;5;2).

 

А. К (4;-2;6) ;       Б. К (8;-4;5) ;       В. К (16;8;10) ;     Г. К (8;4;5) .

 4.     Знайдіть координати середини відрізка АВ – точки К, якщо А(7;4;5) і В(3;2;9).

 

А. К (4;-2;6) ;      Б. К (8;-4;5) ;       В. К (5;3;7) ;        Г. К (8;4;5) .

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1   Знайдіть значення виразу:

  А. 11;   Б.  3;   В.  33;  Г.  1.

1.  Знайдіть значення виразу:

  А. 125;   Б.  45;   В.  9;  Г.  5

1.  Знайдіть значення виразу:

   А. 7;   Б.  28;   В.  4;  Г.  1

2.   Сплав містить 6 % олова.

      Скільки кілограмів олова

      міститься в  42 кг сплаву?

     А.  2,52 кг;      Б.   6 кг; 

     В.  36 кг;         Г. 21 кг.

2.   Сплав містить 25 %  міді.

      Скільки кілограмів міді у

      20 кг сплаву?

      А.  25 кг;       Б.  10 кг; 

        В.  5 кг;         Г.   2,5 кг.

2   Сплав містить 12 % цинку.

     Скільки кілограмів цинку у

     50 кг сплаву?

     А.  42 кг;        Б.   6 кг; 

       В.  12 кг;        Г. 38 кг.

3. З деякої точки А проведена похила, довжина якої 20см, а відстань від даної точки до площини дорівнює 16см. Знайдіть проекцію похилої. 

http://school.xvatit.com/images/8/83/8052011_7.jpg   А.12см;

   Б. 4см; 

   В.см ;

   Г. 36см.          

 

 

http://school.xvatit.com/images/8/83/8052011_7.jpg3.  3.   З точки до площини проведено похилу, проекція якої на площину дорівнює 15см, а відстань від цієї точки до площини становить 8см.  Знайдіть довжину похилої.

   А. 289см;

   Б. 23см; 

   В. 7см; 

   Г. 17см

 

3.    Із деякої точки простору на площину проведено похилу, довжина якої дорівнює 5 см, і перпендикуляр, довжина якого 3 см. Знайдіть довжину проекції похилої.

   А.  4 см; 

   Б.  5 см; 

   В.  3 см; 

http://school.xvatit.com/images/8/83/8052011_7.jpg   Г.  8 см.     

 

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

 

1.   Знайдіть  довжину відрізка

     АВ, якщо А(3;4;5),

     В(6;8;5).

 

       Відповідь 5

 

1.   Знайдіть  довжину відрізка 

      АВ, якщо А(2; - 2; - 3),

     В(4;- 2; - 1).

       Відповідь 2  

     

 

  1.   Знайдіть  довжину відрізка

      АВ, якщо А(5; - 6; 7),

     В(8;- 2; 7).

      Відповідь 5

2. Установіть відповідність

   між  рівняннями (1 - 4) та

 множинами їх  коренів ( А –Д).

 

1

x2 – 4x + 3 = 0

2

x2 + 2x - 3 = 0

3

x2 + 4x + 3 = 0

4

x2 – 2x - 3 = 0

А

  Ø

Б

В

Г

Д

 

 

        1- Д, 2- Г, 3-Б, 4-В

 

2. Установіть відповідність

   між  рівняннями (1 - 4) та

 множинами їх  коренів ( А –Д)

 

1

3x2 – 2x - 5 = 0

2

2x2 - 5x - 7 = 0

3

3x2 - 7x + 2 = 0

4

x2 – 5x + 4 = 0

А

Б

В

Г

 Ø

Д

 

           1- В, 2- Д, 3-А, 4-Б

 

 

2. Установіть відповідність

   між  рівняннями (1 - 4) та

 множинами їх  коренів ( А –Д)

 

1

2x2 - 7x + 5 = 0

2

2x2 - 5x + 2 = 0

3

x2 + 5x - 6 = 0

4

2x2 – x - 1 = 0

А

Б

В

Ø

Г

Д

 

          1- А, 2- Г, 3-Б, 4-Д

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1.  Розв’яжіть рівняння

   3cos2x - 5 cosx + 4 = 0

         Відповідь 2πn, n Z  

1. Розв’яжіть рівняння

   cos2x + 5 cosx - 6 = 0

        Відповідь 2πn, n Z  

1. Розв’яжіть рівняння

    sin2x – 4sinx + 3 = 0

   Відповідь   + 2πn, n Z

 

 

 

 

 

 

 

 

 

 

 

 

Завдання № 11

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Яку  з наведених

    властивостей має

   функція  y = 3 – х2 ?

 

  А. Спадає на множині R.

   Б.  Парна.

   В.  Зростає на множині R.

   Г.  Непарна.

 

1. Яке з наведених тверджень

   є неправильним?

 

А. Функція y=13 - x4 є парною.

Б. Функція y=12 x3 є непарною

В. Функція y=8 x2 зростає на

     множині дійсних чисел.

Г.Функція y= спадає на всій

    області визначення .

 1. Знайдіть область визначення  функції

 f (x) =

   А.

   Б.    

   В.

   Г. 

 

2. Яка з наведених

    рівностей правильна?

   А.  = 9

   Б.   = 0,2

   В.    = - 1

 

   Г.    =

 

2. Яка з наведених рівностей

    правильна?

   А.  = 9

   Б.   = 2

 

   В.    = 2

 

   Г.    = 27

 

2. Яка з наведених рівностей

    правильна?

   А.  = 4

   Б.   = - 1

 

   В.    = 0,2

 

   Г.    = 8

 

3. Розв’яжіть рівняння:

    

 А.    х = 1;    

 Б.    х = - 5; 

 В.    х = - 1 ; 

 Г.    х = 0.

3. Розв’яжіть рівняння:         .

 А.    х =2;    

 Б.    х = 3; 

 В.    х = 216 ; 

 Г.    х = -3.

 

3. Розв’яжіть рівняння:  

    2х = 8.

А. х = 3; 

Б. х = 0,25;  

В. х = 4;  

Г. х = -3.

4.Знайдіть 25% від числа

    900.

А. 90;               Б. 300;               В. 225;             Г. 100.

 

4. Знайдіть 25% від числа

    400.

А. 40;               Б. 200;               В. 25;               Г. 100.

 

4. Знайдіть 25% від числа

    600.

А. 60;               Б. 150;               В. 25;               Г. 300.

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. У шухляді лежить 9

    хустинок, з яких дві – білого

    кольору. Навмання беруть

    одну з них. Яка ймовірність

    того, що вона буде білого

    кольору?

А. ; Б. ;В. ; Г.

  1.  Із 24 олівців, що лежать у

    коробці, п’ять червоних,

    чотири синіх, а решта –

    прості. Яка ймовірність того,

    що навмання вибраний

    олівець буде простим?

А. ;  Б. ;В. ; Г.

1. У коробці є 40 кульок,

    половина з яких чорного

    кольору. Навмання беруть

    одну з них. Яка ймовірність

    того, що вона чорного

    кольору?

А. ;  Б. ;В. ; Г.

2.  Розв’яжіть нерівність:

      .

       А.    ;  

       Б.   ; 

       В.   ;   

       Г.  

2. Розв’яжіть нерівність:

    .

       А.    ; 

       Б.   ; 

       В.   ;   

       Г.    .

 

2. Розв’яжіть нерівність:   

.

       А.    ;    

       Б.   ;              

       В.   ;       

       Г.    .

3. Чому дорівнює об'єм

    циліндра, якщо його

    осьовим перерізом є

    квадрат зі стороною 10см?

http://fizma.net/df/geo/tila/img/img19.gif

А. 250 см3;

Б. 50 см3;

В. 100 см3;   

Г. 15 см3.

3. Чому дорівнює об'єм

    циліндра, якщо його осьовим

    перерізом є квадрат зі

    стороною 4см?

http://fizma.net/df/geo/tila/img/img19.gif

А. 2 см3;

Б. 4 см3;

В. 8 см3;   

Г. 16 см3.

3. Чому дорівнює об'єм

    циліндра, якщо його осьовим

    перерізом є квадрат зі

    стороною 6см?

http://fizma.net/df/geo/tila/img/img19.gif

А. 12 см3;

Б. 54 см3;

В. 36 см3;   

Г. 18 см3.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть інтеграл:  

     .

Відповідь 18

1. Обчисліть інтеграл: 

    

   Відповідь 12

1. Обчисліть інтеграл: 

    

   Відповідь 48

 

2. Установіть відповідність між  виразом  (1 - 4) та  його числовим значенням (А –Д).

 

1

sin ()

2

cos ()

3

tg ()

4

сtg ()

А

Б

 

В

Г

Д

 

         1- В, 2- А, 3-Г, 4-Д

 

2.  Установіть відповідність між  виразом  (1 - 4) та  його числовим значенням (А –Д).

 

1

sin ()

2

cos ()

3

tg ()

4

сtg ()

А

Б

  

В

Г

Д

 

1- А, 2- В, 3-Д, 4-Г

 

2.  Установіть відповідність між  виразом  (1 - 4) та  його числовим значенням (А –Д).

 

1

sin ()

2

cos ()

3

tg ()

4

сtg ()

А

Б

  

В

Г

Д

 

        1- А, 2- Б, 3-Д, 4-Г

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Наведіть повне розв’язання задачі:    Знайдіть довжини    (у м) сторін прямокутної ділянки землі площею 16 а, щоб для її огорожі знадобилось якнайменше паркану ?

 

       Відповідь 40 м і 40 м.

 

Наведіть повне розв’язання задачі:  Яку найменшу кількість метрів паркану потрібно замовити, щоб загородити ділянку землі площею 25 а?

 

 

Відповідь 200 м

Наведіть повне розв’язання задачі: Знайдіть довжини      (у м) сторін прямокутної  ділянки землі площею 36 а, щоб для її  огорожі знадобилось

 якнайменше паркану ?

 

       Відповідь 60 м і 60 м.

 

 

 

Завдання № 12

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Яка з наведених рівностей

    неправильна?

   А.     = 90 0

   Б.     = 45 0

   В.      = 30 0

   Г.    2  = 180 0

1. Яка з наведених рівностей

    неправильна?

   А.     = 90 0

   Б.     = 45 0

   В.      = 270 0

   Г.      = 60 0

 1. Яка з наведених рівностей

      неправильна?

   А.     = 90 0

   Б.     = 45 0

   В.      = 30 0

   Г.    2  = 360 0

 

2. Якій із координатних осей

 належить точка C(0;0;-5)?

        А.   Жодній .

        Б.    Oy

        В.    Ox

        Г.    Oz

2. Якій із координатних осей

   належить точка A(0;-2;0)?

        А.   Жодній .

        Б.    Oy

        В.    Ox

        Г.    Oz

2. Якій із координатних осей 

    належить точка  B(3;0;0)?

        А.   Жодній .

        Б.    Oy

        В.    Ox

        Г.    Oz

3.  Знайдіть критичні точки

     функції f (x), якщо відомо,

     що  f '(х) = x2– 5 х.

       А.    5

        Б.     3,5

        В.     0 ; 5

        Г.  – 5 ; 5

3.  Знайдіть критичні точки

     функції f (x), якщо відомо,

     що  f '(х) = x2– 9 х.

       А.    3

        Б.     4,5

        В.     0 ; 9

        Г.  – 3 ; 3

3.  Знайдіть критичні точки

     функції f (x), якщо відомо,

     що  f '(х) = x2 – х.

       А.    1

        Б.     0 ; 1

        В.     0,5

        Г.  – 1 ; 1

4.  Як знайти 52 %  від числа

      960?

  А.  960: 52;    Б.  ;            В. ;     Г.  960*52

4. Як знайти число, 60 %

    якого дорівнюють 360?

А.  360*60;      Б.   ;            В. ;   Г.  .

 

 

 4.  Як встановити, скільки

      відсотків становить

      число  9 від 96?

 

А.  ;    Б.   ;            В. ;   Г. .

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.Знайдіть корені рівняння

       sin х = .

   А.   (-1)k + 2k , k Z

   Б.   + 2k , k Z

   В.    + k , k Z

   Г.    (-1)k + k , k Z

1.Знайдіть корені рівняння

     6 cos х = 5.

   А. arccos + k , k Z

   Б.   arccos + 2k , k Z

   В. (-1)k arccos + k , k Z

   Г.  Розв’язків немає.

1.Знайдіть корені рівняння

     cos х = .

   А.       +2k, k Z

   Б.   (-1)k + 2k , k Z

   В.    + k , k Z

   Г.    + 2k , k Z

  1.  Зі  слова «трикутник»

    навмання вибирають

    одну літеру. Яка ймовір-

    ність того, що виберуть

   літеру «и»?

 А. ; Б. ; В.; Г.

 

2. Зі  слова «математика»

    навмання вибирають одну

   літеру. Яка ймовірність

  того, що виберуть літеру «а»?

А.; Б. ; В. ; Г.

 

 

  1. Зі  слова «геометрія»

     навмання вибирають одну

    літеру. Яка ймовірність того, що виберуть літеру «е»?

А. ;  Б. ; В.  ; Г.

 

3. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює  5 см, а бічне ребро призми

6 см.

http://img-fotki.yandex.ru/get/5311/136164467.1/0_ca451_8f5ca379_M.png

А. 30 см3  ; 

Б. 16см3;  

В.  25см3;   

Г.  150 см3

 

 

3. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює  6 см, а бічне ребро призми

8 см.

http://img-fotki.yandex.ru/get/5311/136164467.1/0_ca451_8f5ca379_M.png

А. 288 см3  ; 

Б.  48см3;  

В.  92см3;   

Г.  192 см3

 

 

3. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює  3см, а бічне ребро призми

4 см.

http://img-fotki.yandex.ru/get/5311/136164467.1/0_ca451_8f5ca379_M.png

А. 27 см3  ; 

Б.  9см3;  

В.  36см3;   

Г.  64 см3

 

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть інтеграл:  

         

 

    Відповідь 7

1. Обчисліть інтеграл: 

            

      Відповідь

1. Обчисліть інтеграл: 

           

 

     Відповідь 15

 

2. Установіть відповідність 

    між нерівностями (1 - 4) та

    множинами їх розв’язків

    (А – Д).

 

1

8х  > 32

2

- 8х  > 32

3

8х  < 32

4

- 8х  < 32

А

Б

В

Г

Д

    1- Д, 2- В, 3-Б, 4-А

2. Установіть відповідність 

    між нерівностями (1 - 4) та

    множинами їх розв’язків

    (А – Д).

 

1

5х  > 30

2

- 5х  > 30

3

5х  < 30

4

- 5х  < 30

А

Б

В

Г

Д

      1- Д, 2- А, 3-Б, 4-В

2. Установіть відповідність 

    між нерівностями (1 - 4) та

    множинами їх розв’язків

    (А – Д).

 

1

4х  > 20

2

- 4х  > 20

3

4х  < 20

4

- 4х  < 20

А

Б

В

Г

Д

  

 

          1- Б, 2- А, 3-Д, 4-В

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

 

 

 

  1. Наведіть повне розв’яза-

    ння задачі:   З точки А до

    площини проведено дві

   похилі АВ і АС .Знайдіть

   довжини похилих, якщо 

   одна з них на 10 см менша

   від другої, а проекції похи-

   лих дорівнюють 18 см і

   32 см.

     Відповідь  30,40

  1. Наведіть повне розв’язання   задачі: З точки А до площини проведено дві похилі АВ і АС. Знайдіть довжини похилих, якщо  одна з них на 26 см більша від другої, а проекції похилих дорівнюють 12 см і 40 см.

 

Відповідь 15, 41

1.  Наведіть повне розв’яза-

     ння задачі: З точки А до

     площини проведено дві

     похилі АВ і АС . Знайдіть

     довжини похилих, якщо

     похилі відносяться як 1: 2,

     а проекції похилих дорівню-

     ють 1см і 7 см.

 

      Відповідь 4, 8

 

 

 

 

 

 

 

 

 

 

Завдання № 13

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.  Яка з наведених

     нерівностей правильна?

   А.  sin 100 0 > 0

   Б.   cos 130 0 > 0

   В.   tg 20 0 < 0

   Г.   ctg 250 0 > 0

1. Яка з наведених

    нерівностей правильна?

   А.  sin 50 0 < 0

   Б.   cos 225 0 < 0

   В.    tg 60 0 < 0

   Г.    ctg 335 0 > 0

 

 1.  Яка з наведених

      нерівностей правильна?

   А.  sin 80 0 > 0

   Б.   cos 130 0 > 0

   В.    tg 210 0 < 0

   Г.    ctg 310 0 > 0

 

2. Спростіть  вираз (а5)8: а17

А. а23; Б. а6; В. а30 ;  Г. а57 

2. Спростіть  вираз (а4)12 : а8

А. а2; Б. а6; В. а40 ;  Г. а8

2. Спростіть  вираз (а3)10: а12

А. а5; Б. а18; В. а30 ;  Г. а6

3. Знайдіть значення виразу

            .

 

   А.    0,009

   Б.   

   В.    0,003

   Г.    0,3

3. Знайдіть значення виразу 

         .

 

   А.    0,4

   Б.    0,2

   В.    0,0002

   Г.    0,0004

 

3. Знайдіть значення виразу 

               .

   А.    0,00002

   Б.    0,2

   В.    0,5

   Г.    0,00005

4.  На рисунку зображено куб

     ABCDA1B1C1D1. Яка з

     наведених площин перпен-

     дикулярна до прямої  AC?

 

        А.   A1B1C1     

        Б.   ACC1

        В.    BCC1

        Г.    BDD1

 

 

4. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

    наведених прямих перпенди-

    кулярна до площини ACC1?

 

        А.   DD1     

        Б.    B1D1

        В.    BD1

        Г.    DC

 

 

4. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

   наведених прямих перпенди-

   кулярна до площини DCC1?

 

        А.   AA1     

        Б.   A1D1

        В.    D1B

        Г.    BC1

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть загальний вигляд

    первісних для   функції:

    f(x) = x24 + x16 - x -10

А      Б;  

В ;    Г

1. Знайдіть загальний вигляд

    первісних для   функції:

    f(x) = x10 – x8 + x + 13

А  

Б;  

В ;    Г

 

1. Знайдіть загальний

    вигляд первісних для 

   функції:  

 f(x) = x12 – x5 + x + 4

А      Б ;  

В   Г

 

2. При якому значенні  n

   вектори  (8;n;6) і

(4;2;3) перпендикулярні?

 

       А.     -5

       Б.   - 25

       В.      5

       Г.     25

 

2. При якому значенні  n

    вектори  (3;-5;n) і

 (n;1;2) перпендикулярні?

 

       А.     1

       Б.   - 1

       В.   - 5

       Г.      3

 

2. При якому значенні  n

   вектори  (3;-3;n) і (n;5;2) перпендикулярні?

 

       А.     5

       Б.   - 3

       В.   - 5

       Г.      3

 

3. Обчисліть об’єм конуса, висота якого 8 см, а радіус основи 6 см.

А. 36 см3;  

Б.  96 см3; 

В. 48 см3;    

Г. 64 см3.

 

3. Обчисліть об’єм конуса, висота якого 9 см, а радіус основи 5 см.

А. 75 см3;  

Б. 45 см3; 

В. 25 см3;    

Г. 81 см3.

 

3. Обчисліть об’єм конуса, висота якого 4 см, а радіус основи 3 см.

А. 36 см3;  

Б. 4 см3; 

В. 12 см3;    

Г. 12 см3.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Розв’яжіть нерівність: 

          

 Відповідь

 

  1. Розв’яжіть нерівність:

         

 Відповідь

 

1.Розв’яжіть нерівність:  

          

 Відповідь

 

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

   його розв’язками ( А –Д).

 

1

sin х = 1

2

cos х = 0

3

tg х = 0

4

сtg х = - 1

А

+k, kZ

Б

+2k, kZ

В

k , kZ

Г

+k ,kZ

Д

+2k, kZ

 

1- Б, 2- Г, 3-В, 4-А

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

    його розв’язками ( А –Д).

 

1

sin 2х = 0

2

cos 2х = 1

3

tg = 0

4

сtg = 1

А

+k , kZ

Б

2k , kZ

В

k , kZ

Г

+2k ,kZ

Д

,kZ

           1- Д, 2- В, 3-Б, 4-Г

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

    його розв’язками ( А –Д).

 

1

sin х = 0

2

cos х = - 1

3

tg х = 1

4

сtg х = 0

А

+k , kZ

Б

+2k, kZ

В

k , kZ

Г

+k ,kZ

Д

+2k, kZ

 

         1- В, 2- Д, 3-А, 4-Г

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1.  Наведіть повне розв’яза-

      ння задачі:  Функцію

      задано формулою

      f (x) =  х – х3.

    1) Знайдіть критичні точки функції f (x).

    2)  Знайдіть найбільше і найменше значення функції f (x) на відрізку [0; 1]

     Відповідь 1) -, .

2) max f(x)= f ()= ,

 min f(x)= f(1)= .

 

1. Наведіть повне розв’язання

    задачі: Функцію задано формулою f (x) = – 16 х.

    1) Знайдіть критичні точки функції f (x).

    2)  Знайдіть найбільше і найменше значення функції

f (x) на відрізку [-3; 1]

     Відповідь 1) -2,2.

 2)max f(x)= f(-2)= ,

 min f(x)= f(1)=

1.  Наведіть повне розв’яза-

     ння задачі:  Функцію

     задано формулою

     f (x) = – 8 х.

    1) Знайдіть критичні точки функції f (x).

    2)  Знайдіть найбільше і найменше значення функції

f (x) на відрізку [0; 3]

     Відповідь 1) -2,2.

 2)max f(x)= f(0)= 0,

 min f(x)= f(2)= .

 

 

 

 

Завдання № 14

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.  Точка M не лежить у

      площині паралелограма

     ABCD. Яке взаємне

     розміщення прямих MC і

     AB?

 А.Перетинаються .

 Б. Мимобіжні.

 В. Перетинаються або мимо-

      біжні.

 Г.  Паралельні

 

1.  Яка з наведених фігур

      може бути лінією перетину

      двох площин?

 

        А.   Три точки .

        Б.    Відрізок.

        В.    Пряма.

        Г.    Будь-яка лінія. 

 

  1. Через яку з наведених

фігур можна провести

безліч площин?

 

  А. Паралельні прямі .

  Б.  Мимобіжні прямі.

  В. Прямі, що перетинаються.

  Г.    Пряму і точку на ній.

 

2.  Знайдіть найбільший кут

     трикутника, якщо градусні

     міри всіх кутів відносяться

     як 4:6:8.

    А.  600;        Б.  400; 

    В. 1000 ;       Г. 800 .

 

2. Знайдіть найбільший кут

    трикутника, якщо градусні

    міри всіх кутів відносяться

    як 3:4:5.

   А. 600;              Б.  450;

   В. 750 ;             Г. 1050 .

2.  Знайдіть найменший кут

     трикутника, якщо градусні

     міри всіх кутів відносяться

     як 2:3:5.

    А. 540;           Б.  360; 

    В. 900 ;          Г. 180 .

3. Спростити вираз:

  10  + +

   А. 17;   Б.  39;

   В. 19 ;  Г   24.

3. Обчислити:   

      А. 200;       Б.  8000;

      В. 1600 ;     Г.  400.

3. Обчислити: 

  * - .

        А.  1;       Б.  2;

        В.  3 ;      Г.  4.

4.  Скількома способами

     можна з 25 учнів вибрати

     трьох чергових?

    А. ;   Б.  25*3; 

    В.  ;   Г. .

4.  Скількома способами

     можна з 30 учнів вибрати

    трьох чергових?

    А. ;      Б. 30*3;

    В. ;       Г.

4.  Скількома способами

      можна з 18 учнів вибрати

      трьох делегатів на

      конференцію?

    А. ;   Б  ; 

    В.;      Г. 18*3.

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть похідну функції  (х7 + 5x2 – 10x + 4)'=…

 А.   7x6 + 10x - 10

 Б. +x3 – 5x2 + 4x

 В.   7x6 + 10x + 4

 

 Г.   7x6 + 10x

1. Знайдіть похідну функції  (х6 + 3x2 – x + 3)' = …

   А.   6x5 + 6x

   Б.   + x3 + 3x

   В.    6x5 + 6x - 1

 

   Г.    6x5 + 6x + 3

 

1. Знайдіть похідну функції  (х10 + 4x2 +7x - 2)'= …

   А.   10x9 + 8x

   Б. +x3 - 2x

   В.    10x5 + 8x - 2

 

   Г.    10x9 + 8x + 7

 

2.   Знайти множину

      розв’язків  нерівності

  log0,1(2x-5) > log0,1x

 

   А. ;   Б. ;

   В. ;     Г.

 

 

2. Знайти множину розв’язків

    нерівності 

    log3(x-4) log38

 

    А. ;  Б. ;

    В. ;      Г.

 

 

2.   Знайти множину

      розв’язків  нерівності

              log5x < 2

 

 

  А. ;  Б. ;

  В. ;        Г.

 

 

3.  Сторона основи правиль-

     ної трикутної піраміди

     дорівнює 8 см, а бічне

     ребро – 10 см. Знайдіть

     бічну поверхню піраміди.

 

   А.  18см2.

   Б.  24см2.

   В.  28см2.

   Г.  48см2.

3. Сторона основи правиль-

      ної трикутної піраміди

      дорівнює 6 см, а бічне

      ребро – 5 см. Знайдіть

      бічну поверхню піраміди.

   А.  12см2.

   Б.  72см2.

   В.  36см2.

   Г.  45см2.

 

  1. Сторона основи правиль-

       ної трикутної піраміди

       дорівнює 18 см, а бічне

       ребро – 15 см. Знайдіть

       бічну поверхню піраміди.

 

   А.  108см2.

   Б.  36см2.

   В.  225см2.

   Г.  30см2.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Точка B є серединою

    відрізка  AC. Знайдіть

    координати точки C,

    якщо A(1;2;3), B(3;2;1).

 

 

 Відповідь   C(5;2;-1)

  1. Діагоналі паралелограма ABCD перетинаються в точці  O(-3;1;-2). Знайдіть координати  вершини A , якщо 

     C(-1;3;4).

 

      Відповідь  A(-5;-1;-8)

 

  1. Точка M є серединою

      відрізка  PC. Знайдіть

      координати точки P,

      якщо M(-1;3;2),

      C(2;-3;0).      

 

 

 Відповідь  P(-4;9;4)

  1. До кожного виразу (1 - 4)

      доберіть тотожно рівний

      йому вираз ( А –Д).

 

1

(a - 5)*(a +5)

2

(a - 5)2

3

(5 + 2a)2

4

(2a - 5)*(2a + 5)

А

a2- 10a + 25

Б

a2- 25

В

25 + 20a + 4 a2

Г

4a2 + 25

Д

4a2 - 25

 

1- Б, 2-А , 3-В, 4-Д

 

2. Установіть відповідність

    між  виразами (1 - 4) та

    тотожно рівними їм

    виразами ( А –Д).

 

1

(2a - 3)*(3a + 2)

2

(2a - 3)2

3

(3 - 2a)*(3 + 2a)

4

(3 + 2a)2

А

9 + 12a + 4a2

Б

6a2- 5a - 6

В

4a2- 6a + 9

Г

9 – 12a + 4a2

Д

9 - 4a2

1- Б, 2- Г, 3-Д, 4-А

 

  2.До кожного виразу (1 - 4) 

      доберіть тотожно рівний

      йому вираз ( А –Д).

 

1

(a - 8)*(a + 8)

2

(a - 8)2

3

(a - 4)*(a2+4a+16)

4

(a - 4)*(a - 16)

А

a2- 16a + 64

Б

a2- 64

В

a2- 20a + 64

Г

a3 + 64

Д

a3 - 64

 

1- Б, 2-А , 3-Д, 4-В

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

  1.      Розв’яжіть  рівняння  

2 sin 5 х  - = 0.

Відповідь (-1)k + , kZ

  1. Розв’яжіть  рівняння  

2cos 3 х  - = 0.

Відповідь  + , k Z  

  1.       Розв’яжіть  рівняння  

2 sin 5 х  - = 0.

 Відповідь (-1)k + ,kZ

 

 

 

 

 

 

 

Завдання № 15

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = tg x  

 Б. f (x) = cos х    

 В.  f (x) = 

  1.  Г.  f (x) = sin х 
  1. Вкажіть графік якої функції

    зображено на рисунку.

 

 А. f (x) = sin х  Б. f (x) = 

 В. f (x) = tg x    Г. f (x) = x + 1

1.Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = Б. f (x) = sin х   

 В. f (x) = cos х  Г. f (x) =   

2. Яка з наведених фігур не

    може бути паралельною

    проекцією прямокутника?

 

        А.    Паралелограм .

        Б.    Трапеція.

        В.    Прямокутник.

        Г.    Квадрат. 

2. Через яку з наведених фігур

    можна провести площину і до

    того ж тільки одну?

        А.   Три точки .

        Б.    Точку і пряму.

        В.    Дві будь-які прямі.

        Г.    Дві прямі, що мають

                спільну точку.

2.Відомо, що площини і мають одну спільну точку.

  Скільки ще спільних точок

  мають ці  площини  ?

        А.   Жодної .

        Б.    Безліч.

        В.    Тільки дві.

        Г.    Тільки три. 

3.  Чому дорівнює  швидкість

     змінювання функції

 f(t)= t3 – 4t2 у точці  t = 5 ?

       А.     35

       Б.    115

       В.      20

       Г.     70

3.  Чому дорівнює  швидкість змінювання функції 

f (t) = t3+3t2 у точці  t = 4 ?

       А.     48

       Б.   120

       В.      72

       Г.     36

3.   Матеріальна точка

     рухається вздовж осі Ох за

     законом х = х(t). У якому

     з наведених    випадків

     швидкість цієї матеріальної

    точки є сталою?

   А.  х(t) = t2 – 3t ; 

   Б.  х(t) = t3 – 3t2

   В.  х(t) = 3t – t2

   Г.  х(t) = 3t – 32

4.  Значення якого виразу є

     додатним числом ?

А.  sin 300 0    Б.  cos 95 0

 В.  tg 200 0     Г.  ctg 170 0

4.  Значення якого виразу є

     додатним числом ?

А. sin 120 0   Б. cos 210 0

В. tg 100 0     Г. ctg 320 0

4.  Значення якого виразу є

     додатним числом ?

А.  sin 190 0   Б.   cos 300 0

В.  tg  290 0    Г.   ctg 100 0  

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Один з гострих кутів прямо-

    кутного трикутника на 100

    більший від іншого. Знайдіть

    менший з цих кутів.

А. 400;  Б.500;  В.900; Г.100 .

1.Один з гострих кутів прямо- 

    кутного трикутника на 180

    більший від іншого. Знайдіть

    більший  з цих кутів.

А.660;  Б.540;  В.360; Г.480 .

  1. Один з гострих кутів прямо-

    кутного трикутника у 5 разів

   більший від іншого. Знайдіть

   найменший  з цих кутів.

А.900;  Б.450;  В.150 ;  Г.750.

2.   Розв’яжіть нерівність

          2х < 32

А. ;   Б. ;         В.  ;   Г.

2.   Розв’яжіть нерівність

              5х > 5

А. ;       Б. ;         В.   ;      Г.

2.   Розв’яжіть нерівність

     0,7х < 1

А. ;    Б. ;         В.   ;      Г.

 3. Діаметр кулі дорівнює

    10 см.  Знайдіть площу

    поверхні кулі. 

 

   А.  50см2.

   Б.  40см2.

   В.  25см2.

   Г.  100см2

 

3. Площа великого круга кулі дорівнює 4см2. Знайдіть об’єм кулі. 

 

 А.  64см3.

 Б.  16см3.

 В.  32см3.

 Г.  см3

3. Діаметр кулі дорівнює 6 см. 

    Знайдіть площу поверхні

    кулі. 

 

   А.  54см2.

   Б.  36см2.

   В.  72см2.   

   Г.  18см2

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть:  

      *

Відповідь 3

1. Обчисліть: 

   * *

Відповідь 4   

1. Обчисліть:

      *

Відповідь 2   

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

40 %

Б

20 %

В

37,5 %

Г

62,5 %

Д

75 %

     1- Г, 2- Д, 3-В, 4-А

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

40 %

Б

20 %

В

80 %

Г

12,5 %

Д

25 %

          1- Д, 2- А, 3-Г, 4-В

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

60 %

Б

50 %

В

80 %

Г

62,5 %

Д

20 %

 

          1- Б, 2- Д, Г, 4-А

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Розв’яжіть  рівняння      =  x.

Відповідь 4

1. Розв’яжіть  рівняння             = x - 1.

Відповідь5

1.  Розв’яжіть  рівняння      = 4 - x.

Відповідь 2

 

 

 

 

 

 

Завдання № 16

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = x;    Б. f (x) = x + 1;

 В.  f (x) = x + 2;

 Г.  f (x) =  x - 1

  1. Вкажіть графік якої функції

    зображено на рисунку.

 А. f (x) = ;  Б. f (x) = -  x 2;

 В. f (x) = tg x;  Г. f (x) = x + 2

1.Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = x 2;  Б. f (x) = cos х; 

 В. f (x) = - (x – 1)2;

 Г. f (x) = - x 2  

2. Спростіть вираз

      7 - +

А.7;  Б.36 ; В. 5;  Г. 53

2. Спростіть вираз

      5- +   

А. 6;  Б.20 ; В.2;  Г. 52.

2. Спростіть вираз

      6 - +

А. 25;  Б. 7; В.70;  Г. 5

3.  На рисунку зображено прямокутний паралелепіпед ABCDA1B1C1D1. Яка з наведених прямих паралельна площині (ABC)?                                                                         

   А.  DD1.

   Б.  B1D.

   В.  A1C1.

   Г.  C1D.

3. На рисунку зображено куб ABCDA1B1C1D1. Перерізом куба площиною, що проходить через точки A, C, C1, є…                                                   

 А.  Прямокутний

       трикутник.

 Б.  Прямокутник.

 В.  Ромб.

 Г.  Трапеція.  

 

3. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

  наведених прямих паралельна

   площині (AA1B1)?                                                                         

   А.  BC.

   Б.  BD.

   В.  CB1.  

   Г.  C1D.

 

4.  Обчисліть інтеграл:

          

А.; Б. ;  В. ;  Г. 1.

4.  Обчисліть інтеграл:

         

А. ;  Б. ; В. ;  Г. 2.

4.  Обчисліть інтеграл: 

            

А. 19;  Б. 21;   В.;  Г. 20.

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Катет прямокутного трику-

     тника дорівнює 16 см, а

     медіана, що  проведена до

     нього, дорівнює –  2см.

     Знайдіть інший катет

     трикутника.

 А. см;        Б.  8см;

 В   12см ;           Г.  20см.

1.  Катет прямокутного трику-

     тника дорівнює 12 см, а

     медіана, проведена до іншого

     катета, - 13 см.  Знайдіть

     гіпотенузу трикутника.

А   2см;      Б.  5см;             В.  25см ;            Г. 22см.

1.  Катет прямокутного трику-

     тника дорівнює 12 см, а

     медіана, що  проведена до

     нього, дорівнює –  8 см.

     Знайдіть інший катет

     трикутника.

 А.  4см;     Б. 2см;

 В.  8см ;           Г. 8см.

2.   Розв’яжіть рівняння

       log2(3х + 1) = 4

 А. 3;    Б.10 ;   В.5 ;  Г. 1

2.   Розв’яжіть рівняння

       log3(7 - x) = 2

 А. 0;    Б.16 ;   В.7 ;  Г. - 2

2.   Розв’яжіть рівняння

       lg (5х - 15) = 1

 А. 5;    Б.10 ;   В.15 ;  Г. 1

 3.   Діаметр основи конуса

      AB=24 см, а його висота

     SO=9см.Знайдіть твірну

      конуса SB.

  А.  см

  Б.  33см.

  В.  5см.

  Г.  15 см .

 

 

3. Діаметр основи конуса

    AB=8 см, а його висота

   SO=3см.Знайдіть твірну

    конуса SB.

   А.  см

   Б.  10см.

   В.  5см.

   Г.  2 см .

3.   Діаметр основи конуса

     AB=16 см, а його висота 

    SO=6см.Знайдіть твірну

     конуса SB.  

   А.  см

   Б.  10см.

   В.  5см.

   Г.  12 см .

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1.    Обчисліть: 

 

Відповідь 16

1. Обчисліть:     

  Відповідь    

1. Обчисліть:    

 

Відповідь 102   

2. Установіть відповідність

     між функцією (1 - 4) та  її 

    областю визначення ( А –Д).

1

y = x - 4

2

y = x

3

y = x 9

4

y =  x

А

Б

В

Г

Д

 

1- В, 2- А, 3-Б, 4-Д

 

2. Установіть відповідність

    між функцією (1 - 4) та  її 

    областю значень ( А –Д).

1

y = x

 

2

y = x 9

3

y = x -3

4

y = x -4

А

Б

В

Г

Д

1- Б, 2- Г, 3-Д, 4-А

2. Установіть відповідність

    між функцією (1 - 4) та  її 

    областю визначення ( А –Д).

1

y = x 8

2

y =  x

3

y = x -5

4

y =  x

А

Б

В

Г

Д

 

1- Г, 2- А, 3-Д, 4-Б

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1.  Відомо, що cos =   і  <<.Знайдіть sin.

Відповідь

1. Відомо, що sin =   і  <<. Знайдіть cos .

Відповідь

1.  Відомо, що cos =   і  <<. Знайдіть sin.

Відповідь

 

 

 

Завдання № 17

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.  Обчислити:

- 144:(42 – 46) – 12* (-3)   

А  72;   Б 74 ;  В - 71 ;   Г  - 70

 

1. Обчислити:

1,521 : 0,3 – 1,9 * 0,3   

А.0; Б. – 0,063; В) 4,5 ; Г – 0,63

 

1. Обчислити:

- 4,8 : (- 2,6 + 3,4) + 0,8   

А - 7,2;  Б – 5,2 ;  В 5,2;  Г  6,8

 

2.  Знайдіть кутовий коефіцієнт

    дотичної до графіка  функції

     f (x) = 1,5 х2 - 5 у точці

      х0 = 1 ?

  А.  2;   Б. – 1;  В. -2;   Г.  3

2. Чому дорівнює  кутовий коефіцієнт дотичної до графіка  функції  f (x) = 2х - x3

    у точці  х0 = 0 ?

  А.  – 2;  Б. – 1;  В. 0;  Г.  2

 

2.  Чому дорівнює  кутовий коефіцієнт дотичної до графіка  функції  f (x) =  x3 - 2х

      у точці  х0 = 0 ?

   А.  – 2;  Б. – 1;   В. 0;   Г. 1

3. Знайдіть cередню лінію

    трапеції MN, якщо менша 

    основа  BC = 10 см , а більша

    основа AD = 20 см.  

А. 10см; 

Б.  30см;

В. 15см ;

Г.  5см.     

 

3. Середня лінія трапеції

    MN = 12 см, а більша основа

   AD = 14 см. Знайдіть меншу

   основу BC.

А. 2см;

Б. 10см;

В. 26см;

Г. 14см.

3. Середня лінія трапеції

MN = 10 см, а менша основа  BC = 6 см .  Знайдіть більшу основу AD.

 А. 4см;

 Б. 16м;

 В. 12см;

 Г.  14см.   

 

4. Укажіть правильну нерів-

    ність,  якщо а = sin 300,

    b =  cos 300.

   А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

4.  Укажіть правильну  нерів-

     ність, якщо а = sin 1200,

     b =  cos 1200.

    А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

 

4.  Укажіть правильну нерів-

     ність,  якщо а = sin 3000,

     b =  cos 3000.

   А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

              

А.;       Б. ;

В. 4();   Г. ().

 

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

               

А.;        Б. ;

В. 2();   Г. 3().

 

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

              

А.;        Б. ;

В. 10();  Г. ().

 

2.   Знайдіть загальний вигляд

      первісної для функції 

         .

А.  ;               Б.  ; 

В.  ;            Г.  .

2.   Знайдіть загальний вигляд

      первісної для функції 

       .

 А.   ; 

 Б.   ;            

 В.    ;  

 Г.   .

 

2.   Знайдіть загальний вигляд

      первісної для функції 

         .

 А.   ;

 Б.   ;  

 В.  ; 

 Г   .

 3. Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 4см, 6см і 8 см.

А. 10см

Б. 2см

В. 18см.

Г. 18см

 

3. Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 2см, 3см і 6 см.

  А.  49см.

  Б.  36см.

  В.  11см.

  Г.  7см.

 

3.  Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 6см, 8см і 10 см.

А. 10см

Б. 24см.

В. 18см.

Г. 14см .

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1.  Розв’яжіть рівняння

       cos 2х = .

Відповідь:

     + k , k Z

1.  Розв’яжіть рівняння

 

            8 sin х = 7.

 

   Відповідь:

  (-1)k arcsin + k , k Z

  1. Розв’яжіть рівняння

            sin 3 х = .

Відповідь:

      (-1)k + , k Z

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

1

2

3

2*5! – 52

4

3! + 2!

А

215

Б

42

В

60

Г

8

Д

90

 

          1- Б, 2- Д, 3-А, 4-Г

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

1

2

3

4*4! – 42

4

3! + 4!

А

30

Б

40

В

60

Г

80

Д

90

 

        1- Д, 2- В, 3-Г, 4-А

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

1

2

3

3*3! – 32

4

2! + 4!

А

30

Б

40

В

26

Г

56

Д

9

 

           1- Г, 2- Б, 3-Д, 4-В

 

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Наведіть повне розв’язання

   задачі: Кулю, радіус якої 10 см,

   перетнуто площиною, що

   розміщена на відстані 6 см від

   центра. Знайдіть площу

   перерізу.

          

    Відповідь:   64см2.

 

1. Наведіть повне розв’язання задачі: Кулю, радіус якої 5 см, перетнуто площиною, що розміщена на відстані 3 см від центра. Знайдіть площу перерізу.

 

Відповідь:   16см2

1. Наведіть повне розв’язання

   задачі:Кулю, радіус якої 15 см,

   перетнуто площиною, що

   розміщена на відстані 9 см від

   центра. Знайдіть площу

   перерізу.

 

 Відповідь:   144см2.

 

 

 

 

Завдання № 18

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

  1. Розгортка  якого  тіла

       зображена на рисунку.

            

 А. Піраміда;    Б. Призма;

  1.  В. Конус         Г.  Куб
  1. Розгортка  якого  тіла

    зображена на рисунку.

         

 А. Піраміда;    Б. Призма;

 В. Конус         Г.  Куб

  1.   Розгортка  якого  тіла

      зображена на рисунку.

         

 А. Піраміда;    Б. Призма;

 В. Конус         Г.  Куб

 

2.  Яке з наведених чисел не

   належить області  визначення

   функції  f (x) = ?

 А.  – 2;   Б. – 4;   В. 0;    Г. 1.

2. Яке з наведених чисел не

  належить області  визначення

 функції  f (x) = ?

А. 2;   Б.  – 5;   В.  5;     Г.  7

 

2. Яке з наведених чисел не

  належить області  визначення

  функції  f (x) = ?

 А.  1;  Б. 0;    В. – 3;   Г.  – 7 

3. Знайдіть радіус кола, якщо

    довжина кола дорівнює

    46см.

  А. 23см;     Б.  92см; 

  В. 46см ;         Г.  23см.     

 

3. Знайдіть радіус кола, якщо

    довжина кола дорівнює

    24см.

А. 4см;         Б.  48см;             В. 12см ;           Г.  24см.     

 

3. Знайдіть радіус кола, якщо

    довжина кола дорівнює

    32см.

А. 16см;       Б.  16см;             В. 32см ;           Г.  64см.     

 

4. Обчисліть інтеграл: 

     А. 4;  Б. ;  В. ;  Г.0 .

4.  Обчисліть інтеграл:  

     А.1;  Б. ;  В. ;  Г.0 .    

 

4. Обчисліть інтеграл: 

    А. ;  Б.1;  В. ;  Г.0

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Дано вибірку : 3,6;  3,6;  3,5;

    3,1;  3,6;  3,5;  3,4;  3,7. 

   Знайдіть моду цієї вибірки.

 А. 3,6;  Б. 3,7;   В. 3,5;  Г. 3,4.

 

1. Медіаною сукупності

   даних:  2; 7; 9; 11; 15

   є число

  А.  7;  Б.10;  В. 11;  Г. 9

1. Медіаною сукупності

    даних:  5; 7; 9; 11; 13; 15;17

    є число

  А.  12;  Б.9;  В. 11;  Г. 10  

2.   Знайдіть критичні точки

    функції  

  А. 0;           Б.  - 3 і 3;

  В. 0 і 3 ;     Г.    0 і 9.

 

2.  Знайдіть критичні точки 

  функції 

  А. 0;             Б.  - 3 і 1;

  В.  - 1 і 3 ;    Г.    1 і 3.    

 

2.   Знайдіть критичну точку

      функції  

          

  А. - 1;         Б.   1;

  В.   4 ;         Г.   2.

 

3. Діагональ грані  куба  AC = 6см . Знайдіть об’єм куба.                   

   А.  12см3.

   Б.  72см3.

   В.  24см3.

   Г.  216см3.

 

3. Діагональ грані  куба  AC = 4см. Знайдіть об’єм куба.                   

   А.  16см3.

   Б.  64см3.

   В.  4см3.

   Г.  48см3.

 

 

3. Діагональ грані  куба  AC = 5см . Знайдіть об’єм куба.                   

   А.  125см3.

   Б.  50см3.

   В.  10см3.

   Г.  20см3.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Розв’яжіть нерівність: 

          

 Відповідь 

 

  1. Розв’яжіть нерівність:

         

 Відповідь  

 

  1.             Розв’яжіть нерівність:  

          

 Відповідь  

 

 

 

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

+-

2

-+

3

-+

4

--

А

2

Б

3

В

Г

5

Д

7

 

           1-Д, 2- А, 3-Б, 4-В

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

-+

2

+-

3

--

4

+-

А

2

Б

3

В

4

Г

5

Д

6

 

        1- Г, 2- А, 3-Б, 4-В

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

-+

2

-+

3

- -

4

-+

А

2

Б

8

В

4

Г

5

Д

12

 

           1- В, 2-Б , 3-А, 4-Д

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Знайдіть значення виразу 

      cos + ctg (),

     якщо =

                    Відповідь

1. Знайдіть значення виразу 

 4 cos- sin (),

    якщо =

                      Відповідь 3

 

1. Знайдіть значення виразу 

     tg + sin (),

   якщо =

                     Відповідь

 

 

 

Завдання № 19

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Яку формулу використо-

    вують  для обчислення

    об’єму  кулі?

 

А. V =;     Б.V = πR2H; 

В.  V = abc ;      Г.V = πR2H

  1.   Яку формулу використо-

    вують  для обчислення

    об’єму конуса?

Картинки по запросу рисунки по геометрии 10-11 класс

А. V = πR2H;     Б.V = πR2H; 

В.  V = abc ;      Г.  V =

  1. Яку формулу використо-

   вують  для обчислення

   об’єму  циліндра?

А. V = πR2H;     Б.V = πR2H; 

В.  V = abc ;      Г.  V =

2.  Обчисліть:  

  А. ;    Б. ;   В.  ;  Г.

2.  Обчисліть:  

А. ;    Б. ;   В.  ;  Г. .

 

2.  Обчисліть:  

А. ;    Б. ;   В.  ;  Г. .

3. Дослідіть на парність

    функцію   f (x) =  x3 + х6

   А. непарна;         Б. парна;  

   В. ні парна, ні непарна;  

   Г. встановити неможливо 

 

3. Дослідіть на парність  функцію   f (x) =  4x7 - 2х3

  А. непарна;         Б. парна;  

  В. ні парна, ні непарна;  

  Г. встановити неможливо 

3. Дослідіть на парність 

   функцію   f (x) =  x2 - 3х4

  А. непарна;         Б. парна;  

  В. ні парна, ні непарна;  

  Г. встановити неможливо 

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

   А. 670; 

   Б. 230; 

   В. 900;

   Г. 15

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

 

     А. 360; 

     Б.  180;

     В. 720 ;

     Г. 1080 .

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

  А. 690;

  Б.  110; 

  В. 420;

  Г. 1110

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть похідну функції

 f (x) =x5 + x3 + 4х – 2.

   А.   x4 + x2 + х

   Б.   x4 +  3x2 + 4

   В.    x4 +  3 x2 + х

   Г.    x4 +  3 x2 - 2

 

1. Знайдіть похідну функції

f (x) = x3 + x2 – х + 5.

   А.   3x2 +  x – х + 5

   Б.   3x2 +  x – 1

   В.    3x2 +  x – 1

   Г.    3x2 +  2x2 – 1

 

1. Знайдіть похідну функції

f (x) = x4 + 3x3 + х – 2.

   А.   x3 + x2 + х

   Б.   4x3 +  x2 + х – 2

   В.    x3 +  9 x2 + 1

   Г.    x3 +  9 x2 + x

 

  1. Розв’яжіть рівняння:

         log 2  (х+8) = log 2 10  

 

     А. 10;   Б.  8;   В.  2;    Г.  18.

 

2.  Розв’яжіть рівняння: 

           log4(x+2) = 2

 

   А. 18;   Б.  14;   В.  0;    Г.  6.

2.   Розв’яжіть рівняння :

              log3(х-1)=3.

 

      А. 28;   Б. 26;     В. 10;   Г. 8.

 

 3. Знайти повну поверхню

     циліндра з радіусом 4 см і

     висотою 12 см.

   А.  16см2.

   Б.  32см2. 

   В.  268см2.

   Г.  128см2

3. Знайдіть повну поверхню

    циліндра з радіусом 5 см і

    висотою 15 см.

 

   А.  100см2.

   Б.  400см2.

   В.  200см2.

   Г.  150см2

 

3. Знайдіть повну поверхню

    циліндра з радіусом 3 см і

    висотою 10 см.

 

   А.  78см2.

   Б.  300см2.

   В.  250см2.

   Г.  30см2

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Знайдіть скалярний добуток

    векторів і  , якщо: 

,                                                                                

        Відповідь  8                                                                    

 

1. Знайдіть скалярний добуток

    векторів і  , якщо: 

  ,    

Відповідь  14                                                                      

 

1. Знайдіть скалярний добуток

    векторів і  , якщо:

   ,                                                                                 

         Відповідь  5                                                                  

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

 

1

2

3

4

А

1

Б

В

Г

Д

 

           1-А, 2- Д, 3-В, 4-Б

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

2

3

4

А

Б

В

Г

Д

 

        1- В, 2- Г, 3-Д, 4-А

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

 

1

2

3

4

А

Б

 2

В

Г

Д

 

           1- Д, 2-Г , 3-Б, 4-А

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Знайдіть значення виразу     - +

 

         Відповідь 117

1. Знайдіть значення виразу 

 +  +

          Відповідь 36                   

 

1. Знайдіть значення виразу 

++

         Відповідь 22

 

 

Завдання № 20

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

 1.   Яка з наведених рівностей

      правильна?

 А. ;  Б.; 

 В ;    Г .

1.   Яка з наведених рівностей

      правильна?

А.;     Б. ; 

В.;   Г. .

1.   Яка з наведених рівностей

      правильна?

А.;       Б.; 

В. ;  Г..

 2.     Обчисліть:  

         log5125 + lg100

 А. 125;   Б.  25;   В.  5;  Г. 100.

2.    Обчисліть:  

         

А. 100;   Б.  4;   В.  25;  Г.  2.

2.   Обчисліть: 

         log216 – lg1000   

А. 1;   Б.  2;   В.  - 1;  Г.  3.

 3.    Спростіть вираз: 

         .

    А. 1;    Б. 0;    В - 1;   Г.   3.

 3.   Спростіть вираз: 

         .

   А. 1;  Б.  -1;  В. 0;  Г. 3.

3.   Спростіть вираз: 

.

    А.;       Б. ;

    В.  ;     Г. .       

 

 4.     Знайдіть координати середини відрізка АВ – точки К, якщо А(7;4;5) і В(3;2;9).

 

А. К (4;-2;6) ;      Б. К (8;-4;5) ;       В. К (5;3;7) ;        Г. К (8;4;5) .

 4.  Знайдіть координати

середини відрізка АВ – точки К, якщо   А(3;2;9) і В(5;2;3).

 

 А.  К (4;2;6);     Б.  К (8; 4; 12);

В.  К (-1;0; 3);   Г.  К(-2; 0; 6).

4.    Знайдіть координати середини відрізка АВ – точки К, якщо А(10;3;8) і В(6;5;2).

 

А. К (4;-2;6) ;       Б. К (8;-4;5) ;       В. К (16;8;10) ;     Г. К (8;4;5) .

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Знайдіть значення виразу:

   А. 7;   Б.  28;   В.  4;  Г.  1

1   Знайдіть значення виразу:

  А. 11;   Б.  3;   В.  33;  Г.  1.

1.  Знайдіть значення виразу:

  А. 125;   Б.  45;   В.  9;  Г.  5

2   Сплав містить 12 % цинку.

     Скільки кілограмів цинку у

     50 кг сплаву?

     А.  42 кг;        Б.   6 кг; 

       В.  12 кг;        Г. 38 кг.

2.   Сплав містить 6 % олова.

      Скільки кілограмів олова

      міститься в  42 кг сплаву?

     А.  2,52 кг;      Б.   6 кг; 

     В.  36 кг;         Г. 21 кг.

2.   Сплав містить 25 %  міді.

      Скільки кілограмів міді у

      20 кг сплаву?

      А.  25 кг;       Б.  10 кг; 

        В.  5 кг;         Г.   2,5 кг.

3.    Із деякої точки простору на площину проведено похилу, довжина якої дорівнює 5 см, і перпендикуляр, довжина якого 3 см. Знайдіть довжину проекції похилої.

   А.  4 см; 

   Б.  5 см; 

   В.  3 см; 

http://school.xvatit.com/images/8/83/8052011_7.jpg   Г.  8 см.     

 

 

3. З деякої точки А проведена похила, довжина якої 20см, а відстань від даної точки до площини дорівнює 16см. Знайдіть проекцію похилої. 

http://school.xvatit.com/images/8/83/8052011_7.jpg   А.12см;

   Б. 4см; 

   В.см ;

   Г. 36см.          

 

 

http://school.xvatit.com/images/8/83/8052011_7.jpg3.  3.   З точки до площини проведено похилу, проекція якої на площину дорівнює 15см, а відстань від цієї точки до площини становить 8см.  Знайдіть довжину похилої.

   А. 289см;

   Б. 23см; 

   В. 7см; 

   Г. 17см

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

 

  1.   Знайдіть  довжину відрізка

      АВ, якщо А(5; - 6; 7),

     В(8;- 2; 7).

      Відповідь 5

 

1.   Знайдіть  довжину відрізка

     АВ, якщо А(3;4;5),

     В(6;8;5).

 

       Відповідь 5

 

1.   Знайдіть  довжину відрізка 

      АВ, якщо А(2; - 2; - 3),

     В(4;- 2; - 1).

       Відповідь 2  

     

2. Установіть відповідність

   між  рівняннями (1 - 4) та

 множинами їх  коренів ( А –Д)

 

1

2x2 - 7x + 5 = 0

2

2x2 - 5x + 2 = 0

3

x2 + 5x - 6 = 0

4

2x2 – x - 1 = 0

А

Б

В

Ø

Г

Д

 

          1- А, 2- Г, 3-Б, 4-Д

 

2. Установіть відповідність

   між  рівняннями (1 - 4) та

 множинами їх  коренів ( А –Д).

 

1

x2 – 4x + 3 = 0

2

x2 + 2x - 3 = 0

3

x2 + 4x + 3 = 0

4

x2 – 2x - 3 = 0

А

  Ø

Б

В

Г

Д

 

 

        1- Д, 2- Г, 3-Б, 4-В

 

2. Установіть відповідність

   між  рівняннями (1 - 4) та

 множинами їх  коренів ( А –Д)

 

1

3x2 – 2x - 5 = 0

2

2x2 - 5x - 7 = 0

3

3x2 - 7x + 2 = 0

4

x2 – 5x + 4 = 0

А

Б

В

Г

 Ø

Д

 

           1- В, 2- Д, 3-А, 4-Б

 

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Розв’яжіть рівняння

    sin2x – 4sinx + 3 = 0

   Відповідь   + 2πn, n Z

1.  Розв’яжіть рівняння

   3cos2x - 5 cosx + 4 = 0

         Відповідь 2πn, n Z  

1. Розв’яжіть рівняння

   cos2x + 5 cosx - 6 = 0

        Відповідь 2πn, n Z  

 

 

 

Завдання № 21

для проведення комплексної контрольної роботи

з предмета «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

 1.  Яка з наведених

      нерівностей правильна?

   А.  sin 80 0 > 0

   Б.   cos 130 0 > 0

   В.    tg 210 0 < 0

   Г.    ctg 310 0 > 0

 

1.  Яка з наведених

     нерівностей правильна?

   А.  sin 100 0 > 0

   Б.   cos 130 0 > 0

   В.   tg 20 0 < 0

   Г.   ctg 250 0 > 0

1. Яка з наведених

    нерівностей правильна?

   А.  sin 50 0 < 0

   Б.   cos 225 0 < 0

   В.    tg 60 0 < 0

   Г.    ctg 335 0 > 0

 

2. Спростіть  вираз

        (а3)10: а12

А. а5; Б. а18; В. а30 ;  Г. а6

2. Спростіть  вираз

     (а5)8: а17

А. а23; Б. а6; В. а30 ;  Г. а57 

2. Спростіть  вираз

      (а4)12 : а8

А. а2; Б. а6; В. а40 ;  Г. а8

3. Знайдіть значення виразу 

               .

   А.    0,00002

   Б.    0,2

   В.    0,5

   Г.    0,00005

3. Знайдіть значення виразу

            .

 

   А.    0,009

   Б.   

   В.    0,003

   Г.    0,3

3. Знайдіть значення виразу 

         .

 

   А.    0,4

   Б.    0,2

   В.    0,0002

   Г.    0,0004

 

4. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

   наведених прямих перпенди-

   кулярна до площини DCC1?

 

        А.   AA1     

        Б.   A1D1

        В.    D1B

        Г.    BC1

 

4.  На рисунку зображено куб

     ABCDA1B1C1D1. Яка з

     наведених площин перпен-

     дикулярна до прямої  AC?

 

        А.   A1B1C1     

        Б.   ACC1

        В.    BCC1

        Г.    BDD1

 

 

4. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

    наведених прямих перпенди-

    кулярна до площини ACC1?

 

        А.   DD1     

        Б.    B1D1

        В.    BD1

        Г.    DC

 

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть загальний

    вигляд первісних для 

   функції:  

 f(x) = x12 – x5 + x + 4

А      Б ;  

В   Г

 

1. Знайдіть загальний вигляд

    первісних для   функції:

    f(x) = x24 + x16 - x -10

А      Б;  

В ;    Г

1. Знайдіть загальний вигляд

    первісних для   функції:

    f(x) = x10 – x8 + x + 13

А  

Б;  

В ;    Г

 

2. При якому значенні  n

   вектори  (3;-3;n) і (n;5;2) перпендикулярні?

 

       А.     5

       Б.   - 3

       В.   - 5

       Г.      3

 

2. При якому значенні  n

   вектори  (8;n;6) і

(4;2;3) перпендикулярні?

 

       А.     -5

       Б.   - 25

       В.      5

       Г.     25

 

2. При якому значенні  n

    вектори  (3;-5;n) і

 (n;1;2) перпендикулярні?

 

       А.     1

       Б.   - 1

       В.   - 5

       Г.      3

 

3. Обчисліть об’єм конуса, висота якого 4 см, а радіус основи 3 см.

А. 36 см3;  

Б. 4 см3; 

В. 12 см3;    

Г. 12 см3.

 

3. Обчисліть об’єм конуса, висота якого 8 см, а радіус основи 6 см.

А. 36 см3;  

Б.  96 см3; 

В. 48 см3;    

Г. 64 см3.

 

3. Обчисліть об’єм конуса, висота якого 9 см, а радіус основи 5 см.

А. 75 см3;  

Б. 45 см3; 

В. 25 см3;    

Г. 81 см3.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Розв’яжіть нерівність:  

          

 Відповідь

 

  1. Розв’яжіть нерівність: 

          

 Відповідь

 

  1. Розв’яжіть нерівність:

         

 Відповідь

  1.  

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

    його розв’язками ( А –Д).

 

1

sin х = 0

2

cos х = - 1

3

tg х = 1

4

сtg х = 0

А

+k , kZ

Б

+2k, kZ

В

k , kZ

Г

+k ,kZ

Д

+2k, kZ

 

         1- В, 2- Д, 3-А, 4-Г

 

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

   його розв’язками ( А –Д).

 

1

sin х = 1

2

cos х = 0

3

tg х = 0

4

сtg х = - 1

А

+k, kZ

Б

+2k, kZ

В

k , kZ

Г

+k ,kZ

Д

+2k, kZ

 

1- Б, 2- Г, 3-В, 4-А

2. Установіть відповідність

    між  рівнянням (1 - 4) та 

    його розв’язками ( А –Д).

 

1

sin 2х = 0

2

cos 2х = 1

3

tg = 0

4

сtg = 1

А

+k , kZ

Б

2k , kZ

В

k , kZ

Г

+2k ,kZ

Д

,kZ

           1- Д, 2- В, 3-Б, 4-Г

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Наведіть повне розв’язання задачі: Знайдіть довжини      (у м) сторін прямокутної  ділянки землі площею 36 а, щоб для її  огорожі знадобилось

 якнайменше паркану ?

 

       Відповідь 60 м і 60 м.

 

Наведіть повне розв’язання задачі:    Знайдіть довжини    (у м) сторін прямокутної ділянки землі площею 16 а, щоб для її огорожі знадобилось якнайменше паркану ?

 

       Відповідь 40 м і 40 м.

 

Наведіть повне розв’язання задачі:  Яку найменшу кількість метрів паркану потрібно замовити, щоб загородити ділянку землі площею 25 а?

 

 

Відповідь 200 м

 

 

 

Завдання № 22

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = Б. f (x) = sin х   

 В. f (x) = cos х  Г. f (x) =   

1. Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = tg x  

 Б. f (x) = cos х    

 В.  f (x) = 

 Г.  f (x) = sin х 

  1. Вкажіть графік якої функції

    зображено на рисунку.

 

 А. f (x) = sin х  Б. f (x) = 

В. f (x) = tg x    Г. f (x) = x + 1

2.Відомо, що площини і мають одну спільну точку.

  Скільки ще спільних точок

  мають ці  площини  ?

        А.   Жодної .

        Б.    Безліч.

        В.    Тільки дві.

        Г.    Тільки три. 

2. Яка з наведених фігур не

    може бути паралельною

    проекцією прямокутника?

 

        А.    Паралелограм .

        Б.    Трапеція.

        В.    Прямокутник.

        Г.    Квадрат. 

2. Через яку з наведених фігур

    можна провести площину і до

    того ж тільки одну?

        А.   Три точки .

        Б.    Точку і пряму.

        В.    Дві будь-які прямі.

        Г.    Дві прямі, що мають

                спільну точку.

3.   Матеріальна точка

     рухається вздовж осі Ох за

     законом х = х(t). У якому

     з наведених    випадків

     швидкість цієї матеріальної

    точки є сталою?

   А.  х(t) = t2 – 3t ; 

   Б.  х(t) = t3 – 3t2

   В.  х(t) = 3t – t2

   Г.  х(t) = 3t – 32

3.  Чому дорівнює  швидкість

     змінювання функції

 f(t)= t3 – 4t2 у точці  t = 5 ?

       А.     35

       Б.    115

       В.      20

       Г.     70

3.  Чому дорівнює  швидкість змінювання функції 

f (t) = t3+3t2 у точці  t = 4 ?

       А.     48

       Б.   120

       В.      72

       Г.     36

4.  Значення якого виразу є

     додатним числом ?

А.  sin 190 0   Б.   cos 300 0

В.  tg  290 0    Г.   ctg 100 0  

 

4.  Значення якого виразу є

     додатним числом ?

А.  sin 300 0    Б.  cos 95 0

 В.  tg 200 0     Г.  ctg 170 0

4.  Значення якого виразу є

     додатним числом ?

А. sin 120 0   Б. cos 210 0

В. tg 100 0     Г. ctg 320 0

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

  1. Один з гострих кутів прямо-

    кутного трикутника у 5 разів

   більший від іншого. Знайдіть

   найменший  з цих кутів.

А.900;  Б.450;  В.150 ;  Г.750.

1. Один з гострих кутів прямо-

    кутного трикутника на 100

    більший від іншого. Знайдіть

    менший з цих кутів.

А. 400;  Б.500;  В.900; Г.100 .

1.Один з гострих кутів прямо- 

    кутного трикутника на 180

    більший від іншого. Знайдіть

    більший  з цих кутів.

А.660;  Б.540;  В.360; Г.480 .

2.   Розв’яжіть нерівність

     0,7х < 1

А. ;    Б. ;         В.   ;      Г.

2.   Розв’яжіть нерівність

          2х < 32

А. ;   Б. ;         В.  ;   Г.

2.   Розв’яжіть нерівність

              5х > 5

А. ;       Б. ;         В.   ;      Г.

3. Діаметр кулі дорівнює 6 см. 

    Знайдіть площу поверхні

    кулі. 

 

   А.  54см2.

   Б.  36см2.

   В.  72см2.   

   Г.  18см2

 3. Діаметр кулі дорівнює

    10 см.  Знайдіть площу

    поверхні кулі. 

 

   А.  50см2.

   Б.  40см2.

   В.  25см2.

   Г.  100см2

 

3. Площа великого круга кулі дорівнює 4см2. Знайдіть об’єм кулі. 

 

 А.  64см3.

 Б.  16см3.

 В.  32см3.

 Г.  см3

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть:

      *

Відповідь 2   

1. Обчисліть:  

      *

Відповідь 3

1. Обчисліть: 

   * *

Відповідь 4   

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

60 %

Б

50 %

В

80 %

Г

62,5 %

Д

20 %

 

          1- Б, 2- Д, Г, 4-А

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

40 %

Б

20 %

В

37,5 %

Г

62,5 %

Д

75 %

     1- Г, 2- Д, 3-В, 4-А

2. Установіть відповідність 

    між частинами (1 - 4) та

    відсотками А – Д).

1

2

3

4

А

40 %

Б

20 %

В

80 %

Г

12,5 %

Д

25 %

          1- Д, 2- А, 3-Г, 4-В

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1.  Розв’яжіть  рівняння      = 4 - x.

Відповідь 2

 1. Розв’яжіть  рівняння      =  x.

Відповідь 4

1. Розв’яжіть  рівняння             = x - 1.

Відповідь5

 

 

Завдання № 23

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1.Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = x 2;  Б. f (x) = cos х; 

 В. f (x) = - (x – 1)2;

 Г. f (x) = - x 2  

1. Вкажіть графік якої функції

     зображено на рисунку.

 А. f (x) = x;    Б. f (x) = x + 1;

 В.  f (x) = x + 2;

 Г.  f (x) =  x - 1

  1. Вкажіть графік якої

   функції  зображено на

   рисунку.

 А. f (x) = ;  Б. f (x) = -  x 2;

 В. f (x) = tg x;  Г. f (x) = x + 2

2. Спростіть вираз

      6 - +

А. 25;  Б. 7; В.70;  Г. 5

2. Спростіть вираз

      7 - +

А.7;  Б.36 ; В. 5;  Г. 53

2. Спростіть вираз

      5- +   

А. 6;  Б.20 ; В.2;  Г. 52.

3. На рисунку зображено куб

   ABCDA1B1C1D1. Яка з

  наведених прямих паралельна

   площині (AA1B1)?                                                                         

   А.  BC.

   Б.  BD.

   В.  CB1.  

   Г.  C1D.

 

3.  На рисунку зображено прямокутний паралелепіпед ABCDA1B1C1D1. Яка з наведених прямих паралельна площині (ABC)?                                                                         

   А.  DD1.

   Б.  B1D.

   В.  A1C1.

   Г.  C1D.

3. На рисунку зображено куб ABCDA1B1C1D1. Перерізом куба площиною, що проходить через точки A, C, C1, є…                                                   

 А.  Прямокутний

       трикутник.

 Б.  Прямокутник.

 В.  Ромб.

 Г.  Трапеція.  

 

4.  Обчисліть інтеграл: 

            

А. 19;  Б. 21;   В.;  Г. 20.

4.  Обчисліть інтеграл:

          

А.; Б. ;  В. ;  Г. 1.

4.  Обчисліть інтеграл:

         

А. ;  Б. ; В. ;  Г. 2.

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Катет прямокутного трику-

     тника дорівнює 12 см, а

     медіана, що  проведена до

     нього, дорівнює –  8 см.

     Знайдіть інший катет

     трикутника.

 А.  4см;     Б. 2см;

 В.  8см ;           Г. 8см.

1.  Катет прямокутного трику-

     тника дорівнює 16 см, а

     медіана, що  проведена до

     нього, дорівнює –  2см.

     Знайдіть інший катет

     трикутника.

 А. см;        Б.  8см;

 В   12см ;           Г.  20см.

1.  Катет прямокутного трику-

     тника дорівнює 12 см, а

     медіана, проведена до іншого

     катета, - 13 см.  Знайдіть

     гіпотенузу трикутника.

А   2см;      Б.  5см;             В.  25см ;            Г. 22см.

2.   Розв’яжіть рівняння

       lg (5х - 15) = 1

 А. 5;    Б.10 ;   В.15 ;  Г. 1

2.   Розв’яжіть рівняння

       log2(3х + 1) = 4

 А. 3;    Б.10 ;   В.5 ;  Г. 1

2.   Розв’яжіть рівняння

       log3(7 - x) = 2

 А. 0;    Б.16 ;   В.7 ;  Г. - 2

3.   Діаметр основи конуса

     AB=16 см, а його висота 

    SO=6см.Знайдіть твірну

     конуса SB.  

   А.  см

   Б.  10см.

   В.  5см.

   Г.  12 см .

 

 3.   Діаметр основи конуса

      AB=24 см, а його висота

     SO=9см.Знайдіть твірну

      конуса SB.

  А.  см

  Б.  33см.

  В.  5см.

  Г.  15 см .

 

 

3. Діаметр основи конуса

    AB=8 см, а його висота

   SO=3см.Знайдіть твірну

    конуса SB.

   А.  см

   Б.  10см.

   В.  5см.

   Г.  2 см .

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Обчисліть:    

 

Відповідь 102   

1. Обчисліть: 

 

Відповідь 16

1. Обчисліть:     

  Відповідь    

2. Установіть відповідність

    між функцією (1 - 4) та  її 

    областю визначення ( А –Д).

1

y = x 8

2

y =  x

3

y = x -5

4

y =  x

А

Б

В

Г

Д

 

1- Г, 2- А, 3-Д, 4-Б

 

2. Установіть відповідність

     між функцією (1 - 4) та  її 

    областю визначення ( А –Д).

1

y = x - 4

2

y = x

3

y = x 9

4

y =  x

А

Б

В

Г

Д

 

1- В, 2- А, 3-Б, 4-Д

 

2. Установіть відповідність

    між функцією (1 - 4) та  її 

    областю значень ( А –Д).

1

y = x

 

2

y = x 9

3

y = x -3

4

y = x -4

А

Б

В

Г

Д

1- Б, 2- Г, 3-Д, 4-А

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1.  Відомо, що cos =   і  <<. Знайдіть sin.

Відповідь

 1.  Відомо, що cos =   і  <<.Знайдіть sin.

Відповідь

1. Відомо, що sin =   і  <<. Знайдіть cos .

Відповідь

 

 

 

Завдання № 24

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

1. Обчислити:

- 4,8 : (- 2,6 + 3,4) + 0,8   

А - 7,2;  Б – 5,2 ;  В 5,2;  Г  6,8

 

1.  Обчислити:

- 144:(42 – 46) – 12* (-3)   

А  72;   Б 74 ;  В - 71 ;   Г  - 70

 

1. Обчислити:

1,521 : 0,3 – 1,9 * 0,3   

А.0; Б. – 0,063; В) 4,5 ; Г – 0,63

 

2.  Чому дорівнює  кутовий коефіцієнт дотичної до графіка  функції  f (x) =  x3 - 2х

      у точці  х0 = 0 ?

   А.  – 2;  Б. – 1;   В. 0;   Г. 1

2.  Знайдіть кутовий коефіцієнт

    дотичної до графіка  функції

     f (x) = 1,5 х2 - 5 у точці

      х0 = 1 ?

  А.  2;   Б. – 1;  В. -2;   Г.  3

2. Чому дорівнює  кутовий коефіцієнт дотичної до графіка  функції  f (x) = 2х - x3

    у точці  х0 = 0 ?

  А.  – 2;  Б. – 1;  В. 0;  Г.  2

 

3. Середня лінія трапеції

MN = 10 см, а менша основа  BC = 6 см .  Знайдіть більшу основу AD.

 А. 4см;

 Б. 16м;

 В. 12см;

 Г.  14см.   

 

3. Знайдіть cередню лінію

    трапеції MN, якщо менша 

    основа  BC = 10 см , а більша

    основа AD = 20 см.  

А. 10см; 

Б.  30см;

В. 15см ;

Г.  5см.     

 

3. Середня лінія трапеції

    MN = 12 см, а більша основа

   AD = 14 см. Знайдіть меншу

   основу BC.

А. 2см;

Б. 10см;

В. 26см;

Г. 14см.

4.  Укажіть правильну нерів-

     ність,  якщо а = sin 3000,

     b =  cos 3000.

   А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

 

4. Укажіть правильну нерів-

    ність,  якщо а = sin 300,

    b =  cos 300.

   А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

4.  Укажіть правильну  нерів-

     ність, якщо а = sin 1200,

     b =  cos 1200.

    А.  0 < b  < a

   Б.  a  < 0  < b

   В.   0 < a  < b

   Г.   b  < 0  < a

 

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

              

А.;        Б. ;

В. 10();  Г. ().

 

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

              

А.;       Б. ;

В. 4();   Г. ().

 

1.  Звільнитися від ірраціона-

    льності в знаменнику дробу

               

А.;        Б. ;

В. 2();   Г. 3().

 

2.   Знайдіть загальний вигляд

      первісної для функції 

         .

 А.   ;

 Б.   ;  

 В.  ; 

 Г   .

2.   Знайдіть загальний вигляд

      первісної для функції 

         .

А.  ;               Б.  ; 

В.  ;            Г.  .

2.   Знайдіть загальний вигляд

      первісної для функції 

       .

 А.   ; 

 Б.   ;            

 В.    ;  

 Г.   .

 

3.  Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 6см, 8см і 10 см.

А. 10см

Б. 24см.

В. 18см.

Г. 14см .

 3. Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 4см, 6см і 8 см.

А. 10см

Б. 2см

В. 18см.

Г. 18см

 

3. Знайдіть діагональ AC1 прямокутного паралелепіпеда ABCDA1B1C1D1, виміри якого дорівнюють 2см, 3см і 6 см.

  А.  49см.

  Б.  36см.

  В.  11см.

  Г.  7см.

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

  1. Розв’яжіть рівняння

            sin 3 х = .

Відповідь:

      (-1)k + , k Z

 1.  Розв’яжіть рівняння

       cos 2х = .

Відповідь:

     + k , k Z

1.  Розв’яжіть рівняння

 

            8 sin х = 7.

 

   Відповідь:

  (-1)k arcsin + k , k Z

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

2

3

3*3! – 32

4

2! + 4!

А

30

Б

40

В

26

Г

56

Д

9

 

           1- Г, 2- Б, 3-Д, 4-В

 

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

2

3

2*5! – 52

4

3! + 2!

А

215

Б

42

В

60

Г

8

Д

90

 

          1- Б, 2- Д, 3-А, 4-Г

 

2. Установіть відповідність

    між  виразами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

2

3

4*4! – 42

4

3! + 4!

А

30

Б

40

В

60

Г

80

Д

90

 

        1- Д, 2- В, 3-Г, 4-А

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Наведіть повне розв’язання

   задачі:Кулю, радіус якої 15 см,

   перетнуто площиною, що

   розміщена на відстані 9 см від

   центра. Знайдіть площу

   перерізу.

 

 Відповідь:   144см2.

 

1. Наведіть повне розв’язання

   задачі: Кулю, радіус якої 10 см,

   перетнуто площиною, що

   розміщена на відстані 6 см від

   центра. Знайдіть площу

   перерізу.

          

    Відповідь:   64см2.

 

1. Наведіть повне розв’язання задачі: Кулю, радіус якої 5 см, перетнуто площиною, що розміщена на відстані 3 см від центра. Знайдіть площу перерізу.

 

Відповідь:   16см2

 

 

Завдання № 25

для проведення комплексної контрольної роботи  з предмета  «Математика»

 

I варіант

II варіант

III варіант

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

Початковий рівень

за кожну правильну

 відповідь-0,75 б

  1. Яку формулу використо-

   вують  для обчислення

   об’єму  циліндра?

А. V = πR2H;     Б.V = πR2H; 

В.  V = abc ;      Г.  V =

1. Яку формулу використо-

    вують  для обчислення

    об’єму  кулі?

 

А. V =;     Б.V = πR2H; 

В.  V = abc ;      Г.V = πR2H

1. Яку формулу використо-

    вують  для обчислення

    об’єму конуса?

Картинки по запросу рисунки по геометрии 10-11 класс

А. V = πR2H;     Б.V = πR2H; 

В.  V = abc ;      Г.  V =

2.  Обчисліть:  

А. ;    Б. ;   В.  ;  Г. .

2.  Обчисліть:  

  А. ;    Б. ;   В.  ;  Г.

2.  Обчисліть:  

А. ;    Б. ;   В.  ;  Г. .

 

3. Дослідіть на парність 

   функцію   f (x) =  x2 - 3х4

  А. непарна;         Б. парна;  

  В. ні парна, ні непарна;  

  Г. встановити неможливо 

3. Дослідіть на парність

    функцію   f (x) =  x3 + х6

   А. непарна;         Б. парна;  

   В. ні парна, ні непарна;  

   Г. встановити неможливо 

 

3. Дослідіть на парність  функцію   f (x) =  4x7 - 2х3

  А. непарна;         Б. парна;  

  В. ні парна, ні непарна;  

  Г. встановити неможливо 

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

  А. 690;

  Б.  110; 

  В. 420;

  Г. 1110

 

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

   А. 670; 

   Б. 230; 

   В. 900;

   Г. 15

4. Використовуючи властивості

    рівнобедреного трикутника,

    знайдіть кут ABK

 

     А. 360; 

     Б.  180;

     В. 720 ;

     Г. 1080 .

Середній рівень

за кожну правильну

відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

Середній рівень

за кожну правильну

 відповідь-1 б

1. Знайдіть похідну функції

f (x) = x4 + 3x3 + х – 2.

   А.   x3 + x2 + х

   Б.   4x3 +  x2 + х – 2

   В.    x3 +  9 x2 + 1

   Г.    x3 +  9 x2 + x

 

1. Знайдіть похідну функції

 f (x) =x5 + x3 + 4х – 2.

   А.   x4 + x2 + х

   Б.   x4 +  3x2 + 4

   В.    x4 +  3 x2 + х

   Г.    x4 +  3 x2 - 2

 

1. Знайдіть похідну функції

f (x) = x3 + x2 – х + 5.

   А.   3x2 +  x – х + 5

   Б.   3x2 +  x – 1

   В.    3x2 +  x – 1

   Г.    3x2 +  2x2 – 1

 

2.   Розв’яжіть рівняння :

              log3(х-1)=3.

 

      А. 28;   Б. 26;     В. 10;   Г. 8.

 

  1. Розв’яжіть рівняння:

         log 2  (х+8) = log 2 10  

 

     А. 10;   Б.  8;   В.  2;    Г.  18.

 

2.  Розв’яжіть рівняння: 

           log4(x+2) = 2

 

   А. 18;   Б.  14;   В.  0;    Г.  6.

3. Знайдіть повну поверхню

    циліндра з радіусом 3 см і

    висотою 10 см.

 

   А.  78см2.

   Б.  300см2.

   В.  250см2.

   Г.  30см2

 3. Знайти повну поверхню

     циліндра з радіусом 4 см і

     висотою 12 см.

   А.  16см2.

   Б.  32см2. 

   В.  268см2.

   Г.  128см2

3. Знайдіть повну поверхню

    циліндра з радіусом 5 см і

    висотою 15 см.

 

   А.  100см2.

   Б.  400см2.

   В.  200см2.

   Г.  150см2

 

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

Достатній рівень

за кожну правильну

 відповідь-1,5 б

1. Знайдіть скалярний добуток

    векторів і  , якщо:

   ,                                                                                 

         Відповідь  5                                                                  

 

1. Знайдіть скалярний добуток

    векторів і  , якщо: 

,                                                                                

        Відповідь  8                                                                    

 

1. Знайдіть скалярний добуток

    векторів і  , якщо: 

  ,    

Відповідь  14                                                                      

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

 

1

2

3

4

А

Б

 2

В

Г

Д

 

           1- Д, 2-Г , 3-Б, 4-А

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

 

1

2

3

4

А

1

Б

В

Г

Д

 

           1-А, 2- Д, 3-В, 4-Б

 

2. Установіть відповідність

    між  визначеними

    інтегралами (1 - 4) та  їх 

    значеннями ( А –Д).

 

1

2

3

4

А

Б

В

Г

Д

 

        1- В, 2- Г, 3-Д, 4-А

 

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

Високий рівень

за правильну відповідь-3 б

1. Знайдіть значення виразу 

++

         Відповідь 22

1. Знайдіть значення виразу     - +

 

         Відповідь 117

1. Знайдіть значення виразу 

 +  +

          Відповідь 36                   

 

 

 

 

 

 

 

 

 

 

Середня оцінка розробки
Структурованість
4.8
Оригінальність викладу
4.8
Відповідність темі
4.8
Загальна:
4.8
Всього відгуків: 6
Оцінки та відгуки
  1. Нижборська Наталія
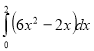
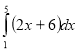
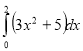
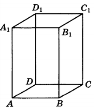
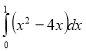
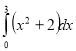
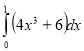
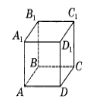
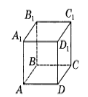
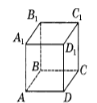
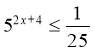
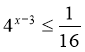
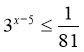
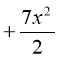
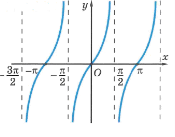
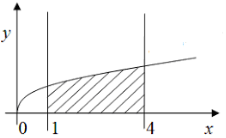
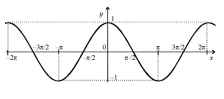
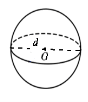
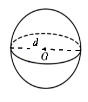
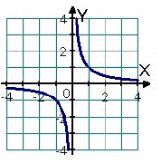
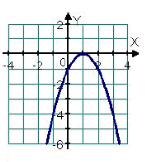
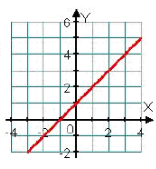
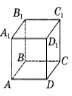
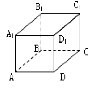
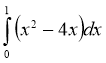
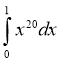
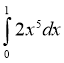
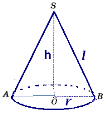
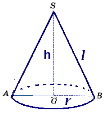
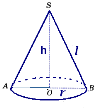
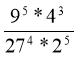
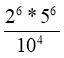
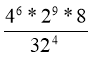
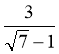
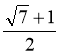
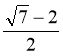
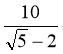
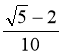
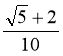
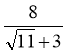
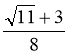
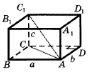
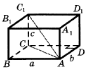
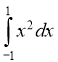
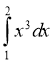
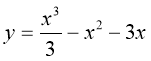
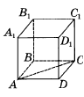
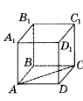
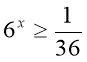
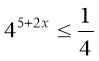
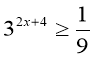
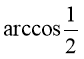
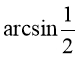
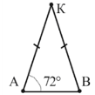
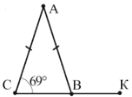
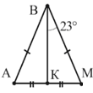
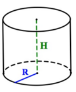
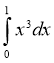
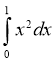
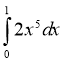
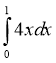
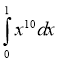
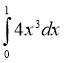
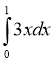
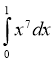
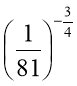
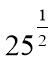
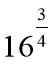
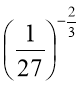
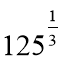
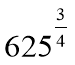
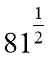
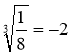
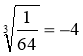
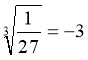
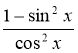
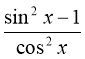
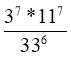
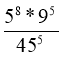
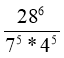
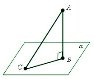
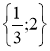
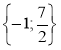
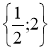
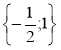
    Нижборська Наталія 17.10.2021 в 16:53
    Світлано Юріївно, дякую за супер-розробку! Низький уклін! Творчості Вам і наснаги!
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
  2. Чижик Наталія Михайлівна
    Чижик Наталія Михайлівна 12.05.2021 в 23:59
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
  3. Бігдан Олена Миколаївна
    Бігдан Олена Миколаївна 15.02.2021 в 22:15
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
  4. Заволокіна Тетяна
    Заволокіна Тетяна 25.11.2019 в 06:09
    Розробка-просто СУПЕР!!! Дякую Вам!
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
  5. Ярощак Ганна Олексіївна
    Ярощак Ганна Олексіївна 15.09.2019 в 13:01
    Загальна:
    4.0
    Структурованість
    4.0
    Оригінальність викладу
    4.0
    Відповідність темі
    4.0
  6. Tanya
    Tanya 25.03.2019 в 11:02
    Загальна:
    5.0
    Структурованість
    5.0
    Оригінальність викладу
    5.0
    Відповідність темі
    5.0
Показати ще 3 відгука
doc
Додав(-ла)
Бойко Світлана Юріївна
Пов’язані теми
Математика, 11 клас, Контрольні роботи
Додано
5 грудня 2018
Переглядів
17840
Оцінка розробки
4.8 (6 відгуків)
Безкоштовний сертифікат
про публікацію авторської розробки
Щоб отримати, додайте розробку

Додати розробку
Рекомендовані матеріали
doc
2617 0
Методична розробка "Прикладні задачі як засіб мотивації навчальної діяльності учнів на уроках математики"
docx
2419 4.7
Факультативний урок .Штучні способи розв’язування рівнянь вищих степенів.
docx
4363 0
Підсумковий урок "Показникові та логарифмічні функції, рівняння та нерівності"
pptx
1283 0
Презентація "Принципи підготовки до ЗНО з математики"
Схожі матеріали
zip
3284 0
Презентація,Впровадження методики
pptx
4478 4.3
Урок -конференція з презентацією на тему «Задачі на знаходження найбільшого та найменшого значень фунції»
ppt
41347 5
Презентація до уроку з математики "Тіла обертання. Циліндр".
doc
4926 5
Застосування визначеного інтегралу до розв’язування фізичних задач
docx
2355 4.3
Математика від А до Я (фрагмент уроку )
Завантажити
Зберегти на потім