Методична розробка "Прикладні задачі як засіб мотивації навчальної діяльності учнів на уроках математики"

Прикладні задачі

як засіб мотивації навчальної діяльності учнів

на уроках математики

Лебедь Ніна Іванівна,

учитель математики Московськобобрицького НВК: ЗОШ І-ІІІ ступенів-ДНЗ

Лебединської районної ради Сумської області

                          « Усі наші задуми, усі пошуки і побудови зводяться                                                          нанівець, якщо немає в учня бажання вчитися»

                                                              В.О. Сухомлинський

Завдання вчителя не доносити істину, а вчити її знаходити. Учня спочатку потрібно зацікавити, навчити хотіти та прагнути, а вже потім – знати і вміти. Процес навчання є своєрідним процесом самостійного «відкриття» учнем вже відомих у науці знань.

Під час навчання математики необхідно систематично збуджувати розвивати і зміцнювати пізнавальний інтерес учнів і як важливий мотив навчання, і як стійку рису особистості. Математика як наука і частина загальнолюдської культури має потужний аксіологічний потенціал, а тому навчання математики у школі має зробити суттєвий внесок у розвиток та соціалізацію особистості учнів, формування їхньої національної свідомості, загальної культури. світоглядних орієнтирів, екологічного стилю мислення і поведінки, творчих здібностей, дослідницьких навичок і навичок життєзабезпечення, здатності до саморозвитку та самонавчання в умовах глобальних змін та викликів.

Навчання математики передбачає формування предметної математичної компетентності. Тобто оволодіння учнями комплексом математичних знань, умінь,навичок, необхідних у повсякденному житті та майбутній трудовій діяльності, достатніх для оволодіння іншими галузями знань і забезпечення неперервної освіти, уміння вчитися впродовж життя.

Тому сучасна українська школа розглядає кожну дитину не стільки як об’єкт. що потребує впливу, скільки як особистість, що інтенсивно розвивається в процесі навчальної діяльності. Реалізація цього не можлива без правильної мотивації навчання та розвитку інтересу до нього. Щоб підтримати іскорку зацікавленості  в учневі, щоб учень займав активну позицію у процесі навчальної діяльності, треба його спонукати робити все з бажанням, а не примушувати, створювати такі умови, які б включали учня до активної пізнавальної діяльності.

Важливу роль у формуванні позитивного ставлення учнів до навчання відіграють як зміст матеріалу, так і його зв'язок з життям та практикою, вміння застосовувати раціональні прийоми під час своєї роботи, проблемний та емоційний характер викладання, організація пошукової., дослідницької пізнавальної діяльності, що дає можливість учням переживати радість відкриття на уроці.

Для багатьох школярів мотиваційним чинником вивчення математики служить її загальновизначна роль у житті та в інших науках. Але є чимало учнів, які на уроці перестають слухати пояснення вчителя, якщо новий матеріал їх не зацікавив з самого початку.

Щоб запобігти байдужості, поява нового матеріалу має відповідати природній допитливості учнів: новий факт не повинен виникати «з нічого» , разом з учнями потрібно з’ясовувати можливість його застосування, а також передбачати його зміст.

Основним засобом здійснення такого підходу є підбір і розгляд на уроці відповідної задачі (вправи, запитання). Класичним прикладом можуть служити прикладні задачі. Задачі прикладного характеру мають важливе значення не тільки для виховання інтересу до навчання, а і для мотивації позитивної навчальної діяльності на уроці та при виконанні домашніх завдань. Розв’язуючи на уроках математики задачі прикладного характеру (економічні, екологічні, фізичні, хімічні, біологічні) та з інших наук і галузей господарства, ми не тільки показуємо важливість математики для науки та повсякденного життя, а й сприяємо появі інтересу до вивчення предмету, спонукаємо до активної навчальної діяльності.

Прикладні задачі виконують:

– освітню функцію, бо їх використання спрямоване на формування у школярів системи знань, умінь, навичок на різних етапах навчання в тому числі і з метою мотивації навчальної діяльності;

– розвиваючу функцію, бо робота з ними розвиває вміння осмислювати зміст понять, застосовувати здобуті знання на практиці, аналізувати результати, розширювати кругозір, робити відповідні узагальнення, порівняння, висновки;

– виховну функцію, бо економічне, екологічне виховання, між предметні зв’язки на уроках математики можуть здійснюватися насамперед через ці задачі.

Крім того, прикладні задачі є одним із основних засобів імплементації наскрізних ліній при вивченні математики.

Застосовуючи прикладні задачі для мотивації навчальної діяльності та враховуючи дефіцит навчального часу, слід дотримуватись таких вимог:

1. задача не повинна бути громіздкою (її розв’язування в класі може займати не більше 5 – 7 хвилин);
2. малюнки та окремі формули мають бути підготовлені на дошці заздалегідь;
3. можна створити комп’ютерну презентацію з метою економії часу та залученням учнів до дослідницької діяльності;
4. оскільки йдеться не про формування навичок, а лише про підведення до нових понять і тверджень, не обов’язково вимагати від учнів повних записів у зошитах розв’язувань таких задач.

Як показує практика, прикладні задачі можна використовувати для мотивації навчальної діяльності на різних етапах уроку математики.

Розглянемо приклади завдань для вмотивування навчальної діяльності учнів при вивченні окремих тем навчального матеріалу з математики.

1. Задача про миттєву швидкість, яка традиційно передує вивченню похідної та демонструє фізичний зміст похідної
2. Задача про дотичну до графіка функції при вивченні геометричного змісту похідної
3. Теоремі про суму кутів трикутника можуть передувати такі проблемні та «провокаційні» запитання до класу:

а) За якої умови трикутник АВС з кутами 58º і 62º, міг би бути рівнобедреним ?

б) В якого трикутника сума кутів більша – у гострокутного чи тупокутного?

4. Вивчення теореми Піфагора можна вмотивувати історичною довідкою про знаменитого древнього вченого та прикладами задач практичного змісту, які доводилося розв’язувати нашим предкам, повідомити, що існує багато способів доведення цієї теореми, запропонувати знайти в різних джерелах інформацію про декілька способів доведення фундаментальної теореми геометрії.
5. Щоб вмотивувати поняття біквадратного рівняння, можна запропонувати учням таку задачу.

Земельна ділянка площею 12 кв.м має форму прямокутника, діагональ якого 5 м. Знайти довжину і ширину ділянки.

6. Введенню поняття логарифма може передувати така задача.

Зараз у колбі 100 бактерій і щодоби їх кількість потроюється. Через скільки діб їх число досягне 24300?.

7. Означенню ірраціонального рівняння  може передувати така геометрична задача.

Фронтон (верхня частина фасаду будівлі) має форму прямокутного   трикутника, сума катетів якого дорівнює 8 м ,а висота проведена з вершини прямого кута., дорівнює 2 м. Знайти площу фронтона.

8. Задачі економічного змісту для мотивації вивчення нерівностей.

Для відпочинку родини влітку потрібно не менше 8000 грн. Кожного місяця сім’я може заощаджувати до 15% сімейного бюджету. Скільки місяців сім’я має відкладати гроші на відпочинок, якщо її щомісячний бюджет  6600 грн. і має поточний рахунок у банку, на який збирається класти заощаджені гроші. Перші півроку із щомісячним нарахуванням 1,5 % від суми, що вкладає у банк?

Задача досить громіздка і тому її можна замінити такою.

Зарплата менеджера з продажу складається: з окладу 500 грн. і 3 % від вартості проданого товару. На яку суму він повинен продати товар, щоб отримати зарплату не менше 2000 грн.?

9. Щоб спонукати учнів вивчати арифметичну та геометричну прогресії, можна запропонувати розв’язати таку задачу.

Робітник обслуговує 16 верстатів-автоматів. Перший він запускає о 8 год., а кожний наступний на 2хв. пізніше. Продуктивність кожного верстата т м/год. Знайти в метрах об’єм продукції, зробленої за 7-годинну зміну.

10. Задачі фізичного змісту допоможуть активізувати навчальну діяльність учнів.

а) при вивченні інтеграла.

Квадратна пластинка зі стороною а  занурена у воду перпендикулярно її поверхні так, що верхня основа пластинки знаходиться на поверхні. Знайти тиск води на пластину.

б)  при вивченні тригонометричних функцій.

Над центром круглого стола радіусом  r  висить лампа. На якій висоті потрібно підвісити цю лампу, щоб на краях стола отримати найбільшу освітленість?.

в)  при вивченні логарифмічної функції.

Якою повинна бути стартова маса ракети, щоб вона досягла космічної швидкості ?.

Коефіцієнт звукоізоляції дерев’яних дверей 20 дБ. У скільки разів вони знижують тиск звуку ?

11. Задачі пов'язані з географічними поняттями можна запропонувати при вивченні тіл обертання.

Радіус Землі 6,4 тис. км. Який шлях проходять за добу внаслідок обертання Землі міста Одеса та Київ, широти яких знайти на карті?

З борту космічного корабля, що перебуває на висоті 400 км над поверхнею Землі, проводиться картографічне знімання певної території. Обчислити:  1) діаметр паралелі, що знаходиться в колі зору космонавта;

2) довжину відповідної паралелі;

3) площу, яку вдається оглянути (вважаючи її спроектованою на площину);

4) кут огляду ( радіус Землі становить 6400 км )

12. Задачі , пов'язані з хімією, допоможуть зацікавити учнів вивчати:

а) Рівняння з двома невідомими.

У процесі повного згоряння вуглеводню маса карбон оксиду, що утворився, втричі більша за масу сполуки, що зоріла. Напишіть формулу вуглеводню.

б)  Відсотки та розв’язувати задачі на відсоткові розрахунки.

Скільки грамів води треба додати до 40 г 25 % розчину сульфатної кислоти, щоб одержати 10 % - й розчин цієї кислоти ?

Приклади залежностей,

 які приводять до поняття показникової функції

“ Деякі види функцій, що найчастіше використовуються,

насамперед показникові, відкривають доступ до багатьох досліджень ”.

                                                                             Леонард Ейлер

Математичними моделями багатьох прикладних задач є показникові рівняння та показникові нерівності. До вивчення показникової функції та її властивостей учнів можуть спонукати приклади залежностей між величинами в різних галузях людської діяльності. Розглянемо прикладні задачі, що підготували учні 11 класу, працюючи над навчальним проектом «Показникові рівняння та нерівності. Методи їх розв’язування»

1. Кількість у мешканців мільйонного міста через  х  років обчислюється за формулою 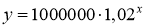(за умови, що щорічний приріст населення 2% ).
2. Температура піску Т масою 100 г, нагрітого до 100º С, змінюється при 0º С залежно від часу  t  за формулою .
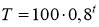3. Під час витікання рідини з циліндричної посудини через тонку трубку в основі циліндра висота h рівня води з часом t змінюється за формулою .
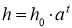4. Моделі “швидкого” та “повільного” зростання.
5. Характеристика обсягу продажу товару визначається за формулою 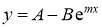, де х – час у роках, у – кількість %, яка визначає частку цього товару на ринку серед інших товарів подібного призначення.

Прикладні задачі математичними моделями

яких є показникові функції, рівняння та нерівності

1.   Задача про радіоактивний розпад

Після скількох періодів піврозпаду з 64 г радіоактивної речовини залишиться 8 г ?

Математична модель .

2.                   Задача про розмноження бактерій

Зараз у колбі 100 бактерій і щодоби їх кількість потроюється. Через скільки діб число бактерій у колбі буде більше 24300 ?

Математична модель .

3.                   Задача про зміну атмосферного тиску

Атмосферний тиск змінюється залежно від висоти  h  над рівнем моря за законом .

Прикладами таких задач є задачі: про вакуумування; про приріст деревини; про реакцію організму людини на дію ліків; про питому радіоактивність рештків організмів при розкопках; про щорічний приріст продукції.

Як показує практика, прикладні задачі можна використовувати для мотивації навчальної діяльності на різних етапах уроку математики: для початку роботи, для мотивації виконання роботи, закріплення та підведення підсумків навчальної діяльності.