ЗБІРНИК ЗАВДАНЬ ДЛЯ ПІДГОТОВКИ ТА ПРОВЕДЕННЯ І ЕТАПУ ВСЕУКРАЇНСЬКИХ ОЛІМПІАД З МАТЕМАТИКИ

 

 

 

 

 

ЗБІРНИК ЗАВДАНЬ

ДЛЯ ПІДГОТОВКИ ТА ПРОВЕДЕННЯ

І ЕТАПУ ВСЕУКРАЇНСЬКИХ ОЛІМПІАД

З   МАТЕМАТИКИ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

           Даний посібник призначений для підготовки та

       проведення І етапу Всеукраїнських олімпіад з

       математики.

           Рекомендовано вчителям математики, керівникам

       методичних об'єднань, молодим вчителям.

 

 

 

 

 

 

РОЛЬ ОЛІМПІАДИ В СИСТЕМІ ПОЗАУРОЧНОЇ РОБОТИ З МАТЕМАТИКИ

 

         Роботу з учнями в позаурочний час можна розмежувати на два типи:

1. Додаткові уроки, що сприяють покращенню засвоєння програмового матеріалу, тобто мають допоміжний характер щодо основних занять.

2. Факультативні та групові заняття, до яких залучаються всі бажаючі учні .

     Незважаючи на необов'язковість  для школяра, другий тип занять заслуговує особливої уваги вчителя. Саме під час  цих занять керівник має змогу залучити учнів до розв'язування нестандартних задач, сприяти успішній участі в математичних олімпіадах.

    На жаль, інколи керівники шкіл вважають, що перемога учнів у математичній олімпіаді повинна бути прямим наслідком гарної роботи вчителя. Насправді ж учитель може лише сприяти успішній участі учнів у таких змаганнях. Учень – відмінник і переможець олімпіади з математики – це зовсім не одне і те ж .

    Для участі в олімпіаді учні повинні мати відповідні знання, бути психологічно та фізично підготовленими, повинні вміти правильно розподіляти час  на виконання завдань, долати можливі труднощі. Разом з тим , такі олімпіади мають велике виховне значення. Вони привчають школярів до організованості, виробляють у них самостійність і гнучкість мислення, зміцнюють віру у свої сили, виховують наполегливість і волю до перемоги.

 

 

 

Але й цього недостатньо. Для досягнення високих результатів у математичних олімпіадах необхідно  мати розвинене нестандартне мислення , чому можуть сприяти факультативні та групові заняття.

    З іншого боку ,складання завдань для математичної олімпіади (або інших типів математичних занять) повинно відповідати певним вимогам.

    Зважаючи на психологічні аспекти треба так складати завдання ,щоб принаймні одну із запропонованих  задач міг розв'язати кожен учасник олімпіади. Але складання варіантів олімпіадних  завдань – це певною мірою мистецтво .

    Збірник складено за паралелями класів. До більшості задач подано відповіді.

   При проведенні шкільної олімпіади доцільно складати завдання з будь-яких п'яти задач даного класу, оцінюючи правильний розв'язок кожної задачі у п'ять балів.

   Посібник рекомендовано вчителям математики, керівникам методичних об'єднань, молодим вчителям, учням 5-11 класів.

 

 

 

 

 

 

 

 

 

                                                              

5  К Л АС         

1. У Марійки 3 брати і 2 сестри. Скільки братів і сестер у її братика Михайлика?

Відповідь: 2 брати і 3 сестри.

2.Знайти суму перших 1000 натуральних чисел.

 Відповідь:499500.

3. Електронний годинник показує два числа: години і хвилини (наприклад: 22:03. Скільки разів на добу ці два числа можуть бути однаковими?

Відповідь: 24р.

4.Андрійкові було 16 років 19 місяців тому, а Миколці буде 19 років через 16 місяців. Хто з них старший за віком? Відповідь: Миколка.

5. Назвемо число «дзеркальним», якщо справа і зліва воно читається так само, як і зліва направо, Наприклад: число 7887 – є «дзеркальним». Знайдіть усі дзеркальні п'ятицифрові натуральні числа , в запису яких використовуються тільки цифри 1 та 0.

6.Скільки прямокутників зображено на малюнку?

 

 

 

7. Петрик купив кілька яблук і приніс їх додому. Сестра запитала його: «Скільки ти заплатив  за ці яблука?» Петрик відповів: «Здогадайся! Я купив у 4 рази більше яблук , ніж ти, але заплатив за кожне яблуко у 3 рази менше». Скільки грошей витратив Петрик , якщо його сестра витратила 6 гривень.

 Відповідь: 8 грн.

8.Різні математичні фігури – це різні цифри, а однакові – однакові цифри. Обчислити:    В+Б+С,  якщо

                          ААБ

   Б

      ВБ5Б

9. Є шестилітрова банка з олією і дві порожні: трилітрова і чотирилітрова. Як налити 1л олії в трилітрову банку?

10.Розшифруйте числовий ребус:  АААА-ВВВ+СС-Д= 1234.

Однакові букви це однакові цифри, різні букви – різні цифри.

 

 

11.На уроці математики Тарас задумав деяке число. Потім поділив його на 7 і до частки додав 7, а результат помножив на 7 і отримав 777. Яке число задумав Тарас?.

Відповідь: 728.

12.Сьогодні неділя. Марічка почала читати книжку у якій 290 сторінок. Вона читає 4 сторінки щодня , крім неділі, коли вона прочитує 25 сторінок. Марічка читає кожного дня. За  скільки днів вона прочитає книжку?

Відповідь:41 д.

13.Уважно вивчи приклади:

  123456789х9=1 111 111 101

  123456789х18=2 222 222 202

Обчисли: 123456789х36=

14. Розв'язати рівняння:  ІхІ -1=5.

 Відповідь: 6; -6.

15. Обчислити : 8 х 9 х 14 + 6 х 12 х 17 +4 х 18  х 19.

Відповідь: 3600.

 

 

16.   Розмістити 10 точок на 5 прямих так, щоб на кожній прямій було по 4 точки.

17.Квиток до музею  коштує 5 грн для дітей і 10 грн для дорослих. У неділю музей відвідали 50 чоловік, які заплатили 350 грн. Скільки дорослих було серед відвідувачів?

Відповідь:20 дорослих.

18.Знайдіть найменше натуральне  число , яке записане тільки одиницями і ділиться на 33.

19.Коли батькові був 31 рік, то сину було 8 років, а тепер батько старший від сина в два рази. Скільки зараз сину років?

Відповідь :23 роки.

20. Промені ОА та ОВ утворюють прямий кут. Петрик провів усередині цього кута промені  ОС та ОД, які утворюють кут 10°. Далі він виміряв усі гострі кути,що утворилися. Виявилося,що сума найбільшого та найменшого з обчислених кутів дорівнює 85°. Знайдіть величини трьох кутів, на які розбивають прямий кут промені ОС та ОД.

Відповідь: 65°, 10° , 15°.

 

                                                  

6  КЛАС

  

1.Перша цифра трьохзначного числа 8. Якщо цю цифру переставити на останнє місце , то число збільшиться на 18. Знайти початкове число.

    Відповідь:890.

 

2.Обчислити : 1-2+3-4+5-6+7-…+1995-1996+1997.  

    Відповідь: 999.

 

3.При якому значенні а рівняння  4 (а-3 ) х = 72 матиме корінь х=6?

 Відповідь:6.

 

4.Довести , що сума двох непарних  послідовних

        чисел ділиться на 4.

 

5.Євген за весну схуд на 20%, потім за літо поправився на 30%, а за осінь знову схуд на 20%, а за зиму поправився на 10%. Поправився чи схуд Євген за рік?.

Відповідь: схуд.

 

6.Доведіть, що сума чисел   і кратна 11.

 

7.Розв'язати рівняння: 2ІхІ + 4=6

 

 Відповідь: 1, -1.

 

 

8.Три роки тому батько був старший за сина в п'ятеро, а тепер – у четверо. Скільки років кожному?

Відповідь: 12р.; 48р.

 

9.Чи можна , маючи  дві посудини 3л і 5л,  набрати з крану 4л  води?

 

10.На біговій доріжці розміщено 12 прапорців на однакових (рівних ) відстанях один від одного. Старт від першого прапорця. Біля восьмого прапорця спортсмен був через 8 секунд після початку бігу. Через скільки секунд при незмінній швидкості він буде біля  дванадцятого прапорця?.

 Відповідь: 12 с.

 

11.Як зміниться дріб, якщо чисельник збільшити на 200%,                   а знаменник зменшити на 50%?

      Відповідь: збільшиться в 6 разів.

 

12.Вага виливки однієї деталі становить 187, 6 кг, а вага обробленої деталі 174 кг. Скільки відсотків ваги виливки становлять стружки металу?

 

 Відповідь:  7,2%.

 

 

 

 

 

13.Учень задумав число. Якщо це число збільшити втроє    і до знайденого добутку додати 0,17, то вийде 2,42. Знайти задумане число.

 

Відповідь: 0,75.

 

14. Обчислити:

+++ + + + + + .

Відповідь:.

15.Довести, що число (3^4п +34) кратне 5.

16.Третина військової роти залишилася на території військової частини, а всі інші її бійці поїхали на стрільби. Бійці цієї роти , що залишилися ,за обідом з'їли четвертину приготовленого борщу, а бійці,що повернулися зі стрільби, отримали порції борщу в півтора рази більші, ніж видавали за обідом. Скільки борщу залишилося для ротної собаки Найди?

Відповідь: для ротної собаки нічого не залишилося.

17.Котра тепер година, якщо до закінчення доби залишилася п'ята частина часу, який пройшов від її початку?

Відповідь: 20 год.

 

18.Стародавня задача. Селянин купив на ярмарку коня, корову та  вівцю. За коня він віддав усіх грошей, за корову -  половину того, що дав за коня, за вівцю останні  5 гривень. Скільки коштує кінь і корова?

 Відповідь: 75грн.

19. Довести,що будь-яке трицифрове число, записане однаковими цифрами ділиться на 37.

20. Простим чи складеним буде число 2002²⁰⁰² +1?

21. Обчислити значення виразу:

-  - -.

Відповідь: 1.

22.Сім'я складається з трьох осіб: батька, матері і сина. На сьогодні сума їхніх років складає 74 роки, а десять років тому ця сума становила 47 років. Скільки зараз років батькові, якщо він старший за сина на 28 років?

Відповідь: 35 років.

23.Різниця двох чисел дорівнює 8 ,а їх сума 42. Знайти ці числа.

Відповідь: 25 і 17.

 

24. Знайдіть останню цифру числа 97531*, якщо  воно  ділиться на 6, але не ділиться на 9.

Відповідь: 8.

 

25.Знайдіть найменше натуральне число, яке ділиться на 12 і має у своєму записі лише цифри 3 та 4 ( кожна з цифр 3 та 4  зустрічається у записі числа принаймні один раз).

Відповідь: 3444.

 

26.У кемпінгу відпочивало М туристів. На обід кожен  турист з'їв половину банки супу, третину банки тушонки та чверть банки квасолі, Відомо, що загалом було з'їдено 156 банок їжі. Скільки всього туристів було у кемпінгу?.

Відповідь: 144.

 

27.Порівняти:

і 

Відповідь:Перший дріб більший.

 

 

7  КЛАС      

1.Спростити:

 2¹⁹х 27³+ 15х4⁹х9⁴  .

   6⁹х10¹⁰+12¹⁰

Відповідь:     7

  2( 5¹⁰+6).

2.Довести ,що сума двох непарних послідовних чисел ділиться на 4.

3.Довести, що число 3^4п+34 кратне 5, якщо п- натуральне число.

4.Периметр трикутника дорівнює 42 см. Медіана ділить його на два трикутника, периметри яких дорівнюють 24см і 28см. Обчислити довжину медіани.

Відповідь: 5см.

5. Розкласти на множники многочлен а⁵ + а +1.

Відповідь: (а²+а+1)(а^3_а²+1).

 

 

6.Довести, що в прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи.

7.Побудуйте графік функції:  У= ІхІ -5.

8.Розв'язати рівняння:    ІхІ =  + 2

Відповідь: х ₁= ; х ₂=4

9. Обчисліть значення виразу:

-+ -+ …+ - .

: -1006.

.Улянка у 27  років мала трьох синів різного віку (вік кожної дитини – натуральне число). Минуло 10 років, і її вік дорівнює сумарному віку її трьох синів. Скільки років нині синам Улянки?

: 11,12 та 14.

 

.Знайдіть усі пари  m і n, які задовольняють рівність

 5m –mn =9n².

: m =12, n =2 або     m = 144, n = 4.

12. Як знайти центр накресленого кола за допомогою креслярського трикутника, що не має сантиметрових

 

рисок,  та олівця ( олівець тільки для проведення прямих ліній).

13. На сторонах АВ, ВС та АС трикутника АВС вибрано точки М, Р і К відповідно таким чином,щоб виконувалися умови ВМ=ВР і СР = СК. Знайдіть величину кута САВ, якщо <КРМ = 40°.

Відповідь: 100°.

 14.Знайдіть число, якщо третина п'ятої частини цього числа менша від третьої частини цього ж  на 60.

Відповідь: 225.

15.Юрко відняв від чисельника і знаменника дробу деякого числа, а Марічка  скоротила дріб, що отримав Юрко, на деяке інше число, отримавши . Яке число відняв Юрко?

Відповідь:11.

16.П'ятеро учасників олімпіади стали її переможцями, отримавши 15,14 та 13 балів, і зайняли відповідно І, ІІ,  ІІІ місця. Скільки учасників зайняли кожне призове місце, якщо разом вони набрали 69 балів?.

Відповідь: 3.

 

17. Я задумав  трицифрове число. Якщо з цифр цього числа скласти можливі двоцифрові числа,а потім їх додати, то третина суми дорівнюватиме задуманому числу. Знайди задумане число.

Відповідь:198.

18.Знайти усі трицифрові числа авс, для яких виконується рівність авс=2(ав+вс+ас).    

Відповідь:134,144,150,228,294. 

19.На дошці записується послідовність чисел 1,2,4,8,16,23,28 і т.д.(кожне наступне число одержується з попереднього, збільшуючи його на суму його цифр). Чи буде записаним на дошці число 11 111 112 003?

Відповідь:Ні.

20. Знайти останні дві цифри числа 21²⁰¹² -11²⁰¹².

Відповідь:20.

21.П'ять цілих чисел записані по колу так, що сума жодних двох чи трьох підряд чисел не ділиться на 3. Скільки чисел серед цих п'яти ділиться на 3?.

Відповідь: 2 числа.

                           

 

     

8  К Л АС             

1.Написавши підряд усі натуральні числа від 1 до 299, утворили число 123456789…297298299. Довести,що воно ділиться на 3.

2.Обчислити суму:

++ ,  якщо хуz=1

Відповідь: 1.

3.Учень задумав двоцифрове  число, в якого цифра десятків на 3   менша від цифри одиниць. Якщо це число поділити на суму його цифр, то в частці буде 4 і в остачі 6. Яке число задумав учень.

 Відповідь: 58.

4.У рівнобедрений трикутник  з кутом 120° при вершині і бічною стороною а вписано коло. Знайдіть радіус кола.

Відповідь: а( – 1,5).

5.Побудувати графік функції у= 4х+ І 2х-6 І.

6. Розкласти на множники: х¹⁰ +х⁵+1.

 

 

7.Розв'яжіть рівняння  4(а²х -1) = 9( а+х) відносно змінної х і вкажіть, при яких значеннях а рівняння має корені.

Відповідь:а, а-1,5

8.Доведіть,що сума чисел хуz+уzх +zху кратна 111.

9.Обчисліть:

(6+1)(6²+1) (6⁴+1)(6⁸+1)(6¹⁶+1) -0,2х6^32.

Відповідь:-0,2.

10.Якою цифрою закінчується сума 54³⁵ +28²¹ ?

Відповідь: 2.

11.Знайти двоцифрове число, коли відомо, що сума його цифр 16, а при перестановці цифр число збільшується  на 18.

Відповідь: 79.

12. Розв'язати систему рівнянь:

Х+У +Z+U =5

У+Z+U+Y=1

Z+U+Y+Х=2

U+Y+Х+У=0

 

Y+Х+У+Z=4

Відповідь: Х=2, У=1,Z =3, U=-1, Y=-2.

13.Розв'язати рівняння:

І х-3І +І х-2 І – І х-4 І =3.

Відповідь: -2; 4..

14.  А  В

 

 Е         С

  Д

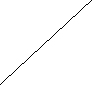
У п'ятикутній зірці, що зображено на малюнку, < АСЕ= <АДБ і <ДБЕ= <ВЕС, ВД=СЕ. Довести , що <АСД= <АДС.

15. Порівняти :      і

16.Знайти усі натуральні значення п, при яких є цілим числом значення виразу  .

Відповідь: 1,2,4,8.

17.У середині трикутника АВС взято точку М,для якої кут МВА =30°, а кут МАВ = 10°. Знайти кут АМС, якщо кут АСВ=80° а АС=ВС.

 

Відповідь:70°

18. Попарно різні числа х,у , u , v задовольняють умову

= . Чому дорівнює сума х + у + u +v ?

Відповідь: 0.

19. Довести що:

- , де п –натуральне число, кратне 17.

20.Знайти усі такі пари натуральних чисел а і в  для якої виконується рівність НСК(а;в) – НСД(а;в) =.

Відповідь: х=20, у=4.

 

 

 

 

 

 

 

 

 

 

 

 

                  

9  К Л АС           

1. Розв'язати нерівність:

| х² – х- 2 | ≥ | х²- 3х – 4 |.

Відповідь: - 2 ; 4.

2. Побудувати графік функції:  У =  .

3.Не розв'язуючи рівняння 5х² – 11х +2 =0 знайти значення виразу х₁³ х₂ + х₁ х₂³, де х₁ і х₂ – корені рівняння.

Відповідь : 8,08.

4.При яких значеннях а рівняння | х² + 6х| = а має два корені?

Відповідь: (9; 0].

5. Обчислити:    -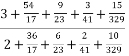 

6. У гострокутному трикутнику АВС довжини всіх сторін виражаються непарними числами. Сторони а і в дорівнюють відповідно 5 і 11. Знайти проекцію сторони с на сторону а.

Відповідь: .

 

 

7.Довести, що  число ціле.    8.Довжини  катетів прямокутного трикутника

дорівнюють а та в. Зовні трикутника на його гіпотенузі як на стороні побудовано квадрат. Знайти відстань від вершини прямого кута трикутника до центра квадрата.

Відповідь:(а+в).

9.Світло на дев'ятому поверсі можна вмикати і вимикати кожним з п'яти вимикачів незалежно один від одного. Вимикачі розміщено  на першому поверсі. Один вимикач не працює. Електромонтер може в будь-якому порядку вимикати та вмикати вимикачі . Як він повинен це робити, щоб електрик на дев'ятому поверсі з'ясував, який вимикач на працює?

10. Одна сторона трикутника дорівнює4 см, а сума двох інших -8 см. Знайдіть невідомі сторони трикутника, якщо довжина кожної з них дорівнює цілому числу  сантиметрів.

Відповідь: 3см, 4 см або 4 см і 4 см.

11.Доведіть , що для будь-яких  додатніх чисел а, в і с виконується нерівність

ав(а+в-2с) +вс(в+с-2а) +ас(а+с-2в)≥ 0.

 

12.Сторони паралелограма дорівнюють а і в, а діагоналі d₁ і d₂ . Відомо, що а⁴ + в⁴ =  d₁ ² d₂ ². Доведіть, що гострий кут паралелограма дорівнює 45°.

13. Відомо,що х₁ і х₂ – корені рівняння  х –( 2а – 3)х +а² -4=0. Знайдіть значення а, при яких виконується рівність 3х₁ +3х₂ =х₁ х₂.

Відповідь: а=1.

14.Розв'яжіть у простих числах рівняння х^z + 1 =y.

Відповідь: х=2, у=5, z=2.

15.Знайдіть таке значення р, щоб один корінь рівняння

 х ²+рх +2р =0 був у двоє більший від другого.

Відповідь: р=0, р=9.

16. На олімпіаді було запропоновано 5 задач і декілька учасників одержали перші премії. Відомо, що ніякі чотири з них не розв'язали в сукупності всі 5 задач, але любі п'ять розв'язали також в сукупності –всі задачі. Скільки чоловік одержали першу премію?

Відповідь : 5.

17.До деякого двозначного числа , яке закінчується на нуль, приписали це саме число. Утворилося нове число, з якого відняли квадрат початкового числа. Різницю

 

поділили на 4% від квадрата початкового числа. У частці отримали половину початкового числа, а в остачі початкове число. Яке число мали на початку?

Відповідь: 50.

18.Довести , що при будь-якому значенні х і у

5у² + 2х² – 4ху -2х – 4у +6 > 0.

19. Спростити вираз:  .

.Попарно різні числа  х,у, u ,v   задовольняють умову 

=

 Чому дорівнює сума х + у+u +v ?

Відповідь: 0.

21.Натуральне число п>18 таке, що числа п-1 та п+1 прості. Доведіть,що п має принаймні вісім натуральних дільників.

 

 

 

 

 

 

 

10  К Л АС                                                 

 

1.У трикутнику з кутом 120° сторони утворюють арифметичну прогресію з різницею 1 . Знайти периметр трикутника.

Відповідь: 7,5 см.

2. Розв'язати рівняння:

( х² – х + 1 )⁴ -10 х²( х² – х +1 )² +9х⁴ =0.

Відповідь:х=2-, х= 2+, х=-1.

3.Розв'яжіть нерівність (х² +1)² – 3( х² +1) <10.

Відповідь: (-2; 2).

4.Попарно різні числа а,в та с задовольняють умову

а² ( в+с) = в²(с+а). Доведіть рівність  с² (а+в ) = а² (в+с).

5. П'ятикутник  АВСДЕ вписаний у коло, при цьому

АВ ІІ АД. Доведіть, що якщо АС² = ВД² + СЕ², то <АВС=90°.

6.Знайти цілі розв'язки нерівності

 

 

х² (х⁴+36) – 6 (х⁴+4)<0.

Відповідь:-1;0;1.

7.Довести, що кожне число виду а⁴+4 є складним , якщо

 а 0.

8. Дано а,в,с і к – натуральні числа. Знайти а,в,с і к якщо

а+=.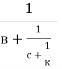

Відповідь:а=87,в=11,с=1,к=1.

9.Обчислити без таблиць і калькулятора:

+.

Відповідь:4.

10.У середині гострого кута лежить точка М . Знайти на сторонах кута такі точки А та В,щоб периметр трикутника МАВ був найменшим.

11.Послідовність 1;4;10;19;31;… має таку властивість, що різниця між сусідніми членами утворює арифметичну прогресію. Знайти п-й член послідовності.

Відповідь:.

 

12.Сторона трикутника дорівнює 10см, а медіани проведені до двох  інших сторін -9см і 12 см. Знайти площу трикутника.

Відповідь:72см².

13.Доведіть , що для будь-якого натурального п значення виразу 4^п + 15п - 1 кратне 9.

14.Доведіть, що для будь-яких додатніх чисел а та в виконується нерівність

(а²+в)( +) ≥4.

15.Побудувати графік функції

У=.

16. У прямокутному трикутнику бісектриса одного з гострих кутів дорівнює  , де с – гіпотенуза.

Відповідь:, с.

17. У рівнобедрений трикутник вписано коло,центр якого віддалений від вершини трикутника на 51см, а точка дотику ділить бічну сторону на відрізки, довжини яких

 

 

відносяться як 8:9, рухаючись від вершини кута при основі. Знайдіть площу цього трикутника.

Відповідь: 3000см^2.

18. У Кіри та Андрія разом 2012 цукерок. Кожну хвилину одночасно Андрій віддає Кірі половину кількості своїх цукерок, а Кіра – усі свої цукерки. Якщо в Андрія стає непарна кількість цукерок,то процес припиняється. Доведіть, що такий процес не може  продовжуватися нескінченно довго.

19.У таблиці 3х3 розставили числа 1,2,3…9 таким чином, що сума чисел у кожному з  дорівнює чотирьох квадратів 2х2 дорівнює S. Знайдіть найбільше можливе значення S.
Відповідь: 24.

20.Дійсний корінь квадратного рівняння ах²+вх.+в=0 помножили на дійсний корінь квадратного рівняння ах²+ах+в=0 і в результаті одержали одиницю. Знайти ці корені.

Відповідь:, або ,.

21. Дано опуклий чотирикутник АВСД такий,що <АВС =90°, АС=СД  і <ВСА=<АСД. Точка Р –середина відрізка АД. Відрізки ВР і АС перетинаються в точці К. Довести, що ВС=СК.

 

                        

     11  К Л АС           

1. Знайти похідну і значення похідної такої функції:

у = х(х-1) (х-2) (х-3)…(х-10) коли х=5

Відповідь: -14400.

2.Знайдіть корінь рівняння: Іх+1І+ІхІ+3Іх-1І-2Іх-2І-х-2=0.

Відповідь:-2, 1.

3.Побудувати графік функції:              у=.

4.Знайдіть усі дійсні числа х і у такі,що х≥у≥1 та

2х² – ху - 3х + у + 1=0.

Відповідь: х=у=1.

5. У правильній чотирикутній піраміді плоский кут при вершині дорівнює. Визначити бічну поверхню піраміди,якщо радіус кола , вписаного в бічну грань, дорівнює

Відповідь: 8tq(+ r).

 

6.Відомо, що  дійсні числа х та у задовольняють умову

+ =4. Чому дорівнює значення виразу ?

.

. Знайдіть усі пари натуральних чисел m та n , що задовольняють рівність  4m+10n= m²+mn+25.

:m=4, n=3.

.На гіпотенузі ВС прямокутного трикутника АВС відмітили точку Р, відмінну від вершин В та С. Коло, описане навколо трикутника АВР,удруге перетинає пряма АС в точці М , а коло, описане навколо трикутника АСР, удруге перетинає пряма АВ у точці К. Доведіть, що точки Р, М, К лежать на одній прямій.

.Для додатніх чисел а,в та с, що задовольняють умову а +в + с ≤, знайдіть найменше можливе значення виразу S= а + в + с +++.

Відповідь: .

10.Довести, що 1²+2²+3²+…+n² =.

 

11.Деяке натуральне число при діленні на 5 і 41 дає остачі , що відповідно дорівнюють 3 і 2. Яка остача буде при діленні цього числа на 205?

Відповідь: 43.

12. З точки А, віддаленої від площини на відстань , проведені до цієї площини похилі АВ і АС під кутом 30° до площини. Їх проекції на площину утворюють кут 120°. Знайдіть ВС.

Відповідь: 3d.

13.Знайдіть усі пари дійсних чисел (х;у), які задовольняють нерівність

    ≤ 3.

Відповідь:(-7;3).

14.Бічна сторона рівнобічної трапеції дорівнює меншій основі. Яким має бути кут при більшій основі трапеції, щоб її площа була найбільша?

Відповідь: 60°.

15.Доведіть ,що >2n+1 , якщо n≥3, n є N.

16.При яких значеннях параметра а нерівність

 

сos ²х- (2а-1)cos + а²- а>0.

Відповідь: а є (-; -1)(2;).

17.Побудувати  графік функції  у =.

Відповідь:Графік – парабола з віками вгору і вершиною в точці (0;1).

18.Знайдіть найменше натуральне число n,для якого виконується рівність

 ++=

Відповідь:105.

19.Нехай АМ і ВР- висоти гострокутного трикутника АВС(<АСВ>45°.) Точки К і Т відкладено на відрізках МА і РВ так, що МК=МВ і РТ=РА. Довести, що КТ=МР.

20.Знайти найменший розв'язок нерівності ≤ +2.

Відповідь: -2.

21.Побудувати графік функції у=(|1+|+|1-|).

 

 

ЗМІСТ

 

Передмова………………………………..

5 клас……………………………………..1-4

6 клас……………………………………..5-9

7 клас …………………………………….10-13

8 клас …………………………………….14-17

9 клас …………………………………….18-21

10 клас …………………………………...22-25

11 клас……………………………………26-29