Зміст і аналіз теми « Тригонометричні рівняння і нерівності» в шкільних підручниках.
Зміст і аналіз теми « Тригонометричні рівняння і нерівності» в шкільних підручниках.
Основним джерелом знань, крім пояснення вчителя, для учнів є підручник. Для того, щоб краще зрозуміти методику вивчення теми «Тригонометричні рівняння і нерівності» потрібно проаналізувати підручники з яких навчаються діти в школі. Проведемо аналіз таких підручників з алгебри та початків аналізу для 10 класу:
- Мерзляк А. Г., Полонський В. Б., Якір М.С. Алгебра і початки аналізу (рівень стандарту) 10 клас.
- Бевз Г. П. Алгебра і початки аналізу (рівень стандарту) для 10-11 класів.
- Нелін Є. П. Алгебра і початки аналізу (рівень стандарту) 10 клас.
- Істер О. С. Математика. Алгебра і початки аналізу та геометрія (рівень стандарту).
- Мерзляк А. Г., Полонський В. Б., Якір М.С. Алгебра і початки аналізу (профільний рівень) 10 клас.
- Мерзляк А. Г., Полонський В. Б., Якір М.С. Алгебра і початки аналізу (рівень стандарту) 10 клас.
- Структура досліджуваної теми.
Тригонометричні рівняння не виділено як окремий параграф, вони включені в параграф «Тригонометричні функції». Окремо виділені такі підтеми:
-
Рівняння
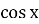 = b;
= b;
-
Рівняння
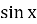 = b і tg x = b;
= b і tg x = b;
- Тригонометричні рівняння, які зводяться до алгебраїчних;
- Виклад теоретичного матеріалу.
На відміну від інших підручників автор подає теоретичний матеріал за схемою: тригонометричне рівняння → обернена тригонометрична функція. Також автор не використовує поняття «найпростіші тригонометричні рівняння» і у параграфах немає визначення, що таке тригонометричне рівняння. У викладі теоретичного матеріалу доцільно використано наочність. Розв’язання тригонометричних рівнянь показано графічним методом за допомогою ілюстрації на графіках тригонометричних функцій, але немає пояснення за допомогою одиничного кола. Також автор не виділяє окремі типи тригонометричних рівнянь, лише наводить приклади окремих рівнянь, що зводяться до алгебраїчних. Підручник недоцільно використовувати для самостійної роботи учнями.
- Система задач
Приклади розв’язування задач наведені після викладення теоретичного матеріалу. До кожної підтеми підібрані завдання для самостійного розв’язування. На мою думку, добір завдань є недостатнім для засвоєння основних понять даної теми. Особливо мало завдань для учнів з середнім рівнем знань. Як відомо, для засвоєння теми потрібно виконати якнайбільше практичних задач, яких в даному підручнику є недостатньо. Що стосується високого рівня , то подано лише декілька однотипних завдань.
- Бевз Г. П. Алгебра і початки аналізу (рівень стандарту) 10 клас.
- Структура досліджуваної теми
Даний підручник адресовано учням класів, у яких на вивчення алгебри і початків аналізу відводиться дві години на тиждень. Тригонометричні рівняння входять до складу теми « Тригонометричні функції». На вивчення даної теми відведено лише один параграф.
- Виклад теоретичного матеріалу
Для ознайомлення учнів з тригонометричними рівняннями автор використав метод наочності і проблемної задачі. Наведено означення тригонометричного рівнянь і лише однієї оберненої тригонометричної функції( арксинуса). Автор не виділяє типи тригонометричних рівнянь, лише дає деякі зауваження щодо складніших рівнянь, що зводяться до найпростіших. Виклад матеріалу подано логічно і зрозуміло. Якщо, для прикладу рівняння ![]() = b учням розповість вчитель, то інші види рівнянь учні зможуть опрацювати самостійно.
= b учням розповість вчитель, то інші види рівнянь учні зможуть опрацювати самостійно.
Недоліком підручника є те, що весь теоретичний матеріал теми «Тригонометричні рівняння» поданий в одному параграфі.
- Система задач.
Після викладу теоретичного матеріалу подано зразки виконання задач «Виконаємо разом» де автори підручника наочно показують виконання завдань, зокрема ілюструють розв’язання на одиничному колі. Недоліком є те, що подано лише по одному завданню різних рівнів складності.
Для подальшого засвоєння матеріалу подано велику кількість завдань для самостійного опрацювання і роботи в класі різних рівнів складності. Варто відмітити практичне завдання №474 і задачі №471, № 472, де потрібно знайти розв’язки рівнянь на графіку.
- Нелін Є. П. Математика. Алгебра і початки аналізу та геометрія, рівень стандарту 10 клас.
- Структура досліджуваної теми.
Тригонометричні рівняння входять до розділу «Тригонометричні функції». На їх вивчення виділено лише один параграф «Найпростіші тригонометричні рівняння». Він поділяється на підпункти:
1) Обернені тригонометричні функції;
2) Розв’язування найпростіших тригонометричних рівнянь;
3) Розв’язування тригонометричних рівнянь, що зводяться до найпростіших.
- Виклад теоретичного матеріалу
Автор подає теоретичний матеріал у вигляді таблиці з основними означеннями. Поняття тригонометричного рівняння вводиться без попереднього пояснення і наочної ілюстрації. Підручник не доцільно використовувати учням для самостійного опрацювання, оскільки він не містить достатніх пояснень матеріалу, не прослідковуються логічні лінії побудови викладу теоретичного матеріалу.
Автор наводить лише один метод для розв’язування рівнянь, що зводяться до найпростіших – метод заміни змінних. Усі інші типи рівнянь і методи їх розв’язування об’єднано в одну групу. Схема розв’язання тригонометричних рівнянь подана за допомогою орієнтирів з зауваженнями і коментарями.
- Система задач.
Після викладу теоретичного матеріалу у кожному параграфі подано приклади розв’язування вправ з вказівками і коментарями. Вправи для виконання в класі і домашнього завдання поділені на рівні. У параграфах достатня кількість завдань різної складності, але немає завдань графічного характеру. Їх мета показати, що у тригонометричних рівнянь – нескінченна кількість розв’язків, що відрізняє їх від усіх інших рівнянь.
- Істер О. С. Математика. Алгебра і початки аналізу та геометрія (рівень стандарту).
- Структура досліджуваної теми
Тригонометричні рівняння вивчаються у розділі «Тригонометричні функції» у параграфі «Найпростіші тригонометричні рівняння». Вивчення теми відбувається за схемою: обернені тригонометричні функції → найпростіші тригонометричні рівняння → рівняння, що зводяться до найпростіших.
- Виклад теоретичного матеріалу
Автор наводить означення обернених тригонометричних функцій, виділяє пояснення до кожного з них. Однак поняття «арккосинус», «арксинус» вводяться без графічної інтерпретації і практичного застосування. Поняття тригонометричних рівнянь і їх розв’язків наведено з допомогою ілюстрації на одиничному колі.
Автор не виділяє окремих методів для розв’язування тригонометричних рівнянь, що зводяться до найпростіших, лише наводить деякі приклади.
- Система задач.
Після кожного означення автор наводить приклади завдань з детальним поясненням розв’язання. У параграфі є достатня кількість завдань і для роботи в класі, і для домашнього завдання, але немає завдань на побудову графіків і інтерпретації розв’язків рівняння на одиничному колі.
- Мерзляк А. Г., Полонський В., Б., Якір М.С. Алгебра і початки аналізу (профільний рівень) 10 клас.
- Структура досліджуваної теми.
Для вивчення тригонометричних рівнянь і нерівностей виділено окремий параграф. Він у свою чергу складається з таких пунктів:
-
Рівняння
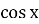 = b;
= b;
-
Рівняння
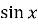 = b;
= b;
- Рівняння tg x= b , ctg x= b;
- Функції y = arcos x, y = arcsin x, y = arctg x, y = arcctg x;
- Тригонометричні рівняння, які зводяться до алгебраїчних;
- Розв’язування тригонометричних рівнянь методом розкладання на множники. Застосування обмеженості тригонометричних функцій;
- Тригонометричні нерівності.
- Виклад теоретичного матеріалу
Для викладу теоретичного матеріалу автор доцільно використав метод наочності. Поняття арккосинуса (арксинуса, арктангенса і арккотангенса) введено з допомогою графічної інтерпретації, що дає змогу сформувати загальне уявлення про нього. Також автор підкреслює особливість тригонометричних рівнянь через нескінченну кількість їх розв’язків, звертає увагу на всі аспекти розв’язання тригонометричних рівнянь.
Виклад матеріалу в даному підручнику є дуже детальним і дає можливість учням самостійно опрацювати тему.
- Система задач.
Після викладу матеріалу наведені конкретні приклади розв’язання задач. Автор надає детальне розв’язання таких прикладів з покроковою інструкцією щодо розв’язання. У параграфі подано багато завдань для розв’язання. Їх добір є дуже різноманітним і для кожного рівня знань є достатня кількість задач. Зокрема є багато вправ достатнього і високого рівнів, що надає змогу учням більше опрацювати і засвоїти кожну тему.
Підручники є важливою складовою навчального процесу і виступають інструментом у руках вчителя. Тому потрібно, щоб усі підручники відповідали навчальним програмам і повністю висвітлювали теоретичний матеріал.


про публікацію авторської розробки
Додати розробку
