МОДУЛЬ ІІ. ПРОСТІ АЛГОРИТМИ.

Лабораторна робота 3. Лінійні алгоритми. (2 год.)

Зміст заняття: Створення першої власної програми, використання операторів read, readln, опис змінних різних типів, форматований вивід.

Задача

Тролейбус рушає з місця з прискоренням a = 1,5 м/с². Яку швидкість він розвине через час t? Яку відстань пройде при цьому?

3.1. Теорія.

Для початку студент повинен знайти розв’язок задачі: зрозуміти, які величини у ній фігурують і розділити їх на дві групи: ті, які відомі, і ті, які невідомі, далі слід визначити послідовність знаходження невідомих величин і, якщо є така потреба, вивести формули для їх розрахунку. У нашій задачі:

v = at; 

S = at²/2 = vt/2.

Далі слід визначити тип і вид даних - величин, що будуть використовуватися при програмуванні задачі. Прості величини діляться на константи і змінні. У свою чергу, всі змінні діляться на типи: тип визначає, у якому вигляді змінна зберігається у комп’ютері і яких значень може набувати.

Деякі прості типи (до складних типів перейдемо згодом):

1.     Цілі типи (ShortInt, Integer, LongInt, Byte, Word).

2.     Дійсні типи (Real, Single, Double, Extended, Comp).

3.     Логічний (Boolean).

4.     Символьний (Char).

5.     Стрічковий (String).

Якщо змінна у процесі виконання програми може набувати дробових значень, використовується у виразах з множенням, діленням, математичними функціями, то її слід описати як змінну дійсного типу; якщо її значення – буква, то це – символьна змінна; якщо значення – слово, то змінна – стрічкового типу. Різниця між типами однієї групи тонка, для початку можна, не вникаючи в деталі, використовувати у якості цілої змінної змінну типу Integer, а у якості дійсної – змінну типу Real.

3.2. Оператори read, readln.

           Оператор read

Оператор read має вигляд:

read(<змінна>, <змінна>, . . . , <змінна>)

Оператор read приймає інформацію з вхідного потоку (клавіатури), інтерпретує її як значення і присвоює ці значення відповідним змінним (при вводі з клавіатури інформація попадає у вхідний потік програми тільки після того, як натиснута клавіша Enter; якщо при наборі зроблено помилку і інформація ще не направлена у вхідний потік, можна скористатися клавішою Backspace для внесення змін, а після натискання Enter змінити значення вже не можна).

Кількість значень і порядок їх появи у вхідному потоці повинні строго відповідати списку змінних в операторі read. Якщо ці значення - числа, кожне з них набирається за правилами запису чисел. Між значеннями у вхідному потоці має стояти один чи кілька пробілів або символів нового рядка (натиснута клавіша Enter). Якщо при зчитуванні даних оператор read не виявляє в рядку числа, він зчитує наступну стрічку і т.д. Якщо ж число набрано невірно або в його записі є неприпустимі символи (наприклад, кома чи крапка з комою), програма припиняє роботу і видає повідомлення про помилку (invalid numeric format).

Оператор readln після вводу інформації переводить курсор у наступний рядок.

Оператор readln; (без аргументів) переводить систему в стан очікування  робота програми переривається і комп’ютер чекає натискання клавіші Enter. Після цього програма продовжує роботу. Цей оператор потрібний для того, щоб після виконання програми ми залишилися у вікні виконання програми (інакше після завершення програми це вікно закривається і система повертається у вікно редагування).

3.3. План програми 

Для написання логічно стрункої та правильної програми слід скласти план – послідовність дій, виконання яких приведе до розв’язку поставленої задачі. Для задачі, що розглядається, він виглядає так:

1.   Описати константи і змінні a, t, v, S.

2.   Ввести значення змінних t, a.

3.   Обчислити значення змінних v, S.

4.   Вивести результати обрахунків v, S.

          програма

program Troll; {pochatok}{v takyx dugkax pywut komentari}

                            

const       {opys nezminnyx danyx - konstant}     a=1.5; 

var         {оpys zminnyx}     t,v,s:real;

begin  {pochatok osnovnogo textu programy chastyny wcho vykonyje diji}   write(‘ vvedit chas t    ’); {“pidkazka" do vvodu}  read(t);                     { vvid }   v:=a*t;   s:=v*t/2;

 writeln(‘Za’,t,’sekund wvydkist trolejbusa v=’,v,’m/s’);           {vyvedennia na ekran}

 writeln(‘ trolejbus projde vidstan S=’,s,’ m’); readln;

end.                     { kinec programy}     

У фігурних дужках для зручності користувача написані коментарі, комп’ютер їх ігнорує (при наборі програми їх можна випустити).  Комп’ютер виконує оператори нашої програми Troll послідовно, один за іншим. Спочатку буде виконуватися перший оператор write. При цьому на екрані з’явиться «підказка» користувачу, будуть виведені слова: vvedit chas t . Потім почнеться виконання оператора вводу з клавіатури: read(t). Комп’ютер при цьому буде очікувати вводу з клавіатури числа (оскільки змінна t – дійсного типу). Після його (числа) вводу і натискання клавіші вводу (Еnter), змінна t набуде значення, введеного з клавіатури. Потім послідовно будуть вирахувані значення змінних v і s. Оператори writeln в кінці програми виведуть на екран змінні t, v, s.

Пригадайте, якщо у операторі writeln набір символів записаний у апострофах (це так звана стрічкова константа), то ці символи будуть виведені на екран без змін, окрім апострофів, якщо ж у списку міститься ім’я змінної (наприклад, t), то буде виведене її значення. Тобто оператор writeln(t); виведе на екран з нового рядка значення змінної t, тобто число, а оператор writeln(‘t’); виведе на екран з нового рядка символ t. Якщо t = 2, то оператор writeln(‘t=’, t) виведе на екран у новому рядку таке: t=2.

Г) Контрольний приклад

a = 1.5     t = 1 v = 1.5    S = 0.75 

2. Запис констант з порядком

Для запису чисел в Pascal'і використовуються три форми. Ціле число записується у вигляді послідовності цифр і знаку мінус (для від’ємних чисел). Наприклад: 345  або  -15. Для запису дробових чисел використовується десяткова крапка: 3.1415926  або  -2.718. Дуже великі числа в алгебрі прийнято представляти у вигляді степенів числа 10. У мовах програмування такий запис теж практикується і називається він нормалізована (експоненційна) форма. Тому дуже великі і дуже малі числа як правило записуються в експоненційній формі: 

Наприклад, число -1.1710⁸ записується як   -1.17E+08 або -1.17E8, при цьому

                      -                                1.17                             Е                      +08

Знак мантиси Мантиса - число від 1 до 10 Символ 10 Порядок зі знаком

Латинські букви "E" і "e" не розрізняються!

Показник степеня, котрий ставиться після латинської літери "Е", може бути тільки цілим. Мантиса (число перед літерою Е) повинна бути обов’язково: число 10⁹ записується як 1е9, а запис е9 сприймається машиною як ім’я, а не як число. Інші приклади: алгебраїчний запис запис на мові Паскаль

9.110-21	9.1E-21
-0.17103	-0.17E3 чи –1.7E2
105	1E5

3.Форматований вивід

Інформація, яку виводить будь-яка програма, повинна легко читатися і бути зрозумілою користувачу. Наприклад, дійсні числа повинні виводитися у звичній формі – як число з крапкою, у записі потрібні пробіли, щоб відділити число від тексту і т.д. З цією метою мови програмування використовують формати.

           Формати виводу даних.

При виводі значень на екран можна вказувати формат, тобто відводити поле для розміщення цих значень. Формати для даних різних типів:

1.               Для стрічкових і символьних даних - формат задається одним числом, що визначає число позицій, котрі відводяться на значення цих даних (тобто на символ чи набір символів).

2.               Для цілих даних - формат задається одним числом, що визначає число позицій, що відводяться на це число.

3.               Для дійсних даних - формат задається або одним числом, що визначає число позицій, що відводяться на це число у експоненційній формі; або двома числами, перше з яких позначає загальний розмір поля, відведеного під це число, друге - число знаків після коми. Приклади використання форматованого виводу показані нижче. Зліва неведена програма, результати її виводу на екран показані справа.

 

Задача 2.

Визначити енергію електрона у атомі водню на орбіті з номером n.

Теорія: Шукана енергія визначається за формулою E = –(m_ee⁴)/(8ε₀²h²)n^-2, де m_e і е – маса і заряд електрона, ε₀ и h- діелектрична стала і стала Планка. В програмі опишем постійні величини як константи, номер орбіти введем з клавіатури:

program energy; const    m=9.109e-31;    e=1.602e-19;    e0=8.854e-12;    h=6.626e-34; var   en:real;   n:integer; begin

  Write('Vvedit nomer orbity');   read(n);

  En:=-m*sqr(e*e/(e0*h*n))/8;   writeln('   E(',n:2,' )=', en:12); end.

4.Самостійна робота

Кожен студент отримує задачу з розділу 1 додатку. Завдання студента - написати і відлагодити просту програму, котра розв’язує цю задачу і містить оператори присвоєння, вводу з клавіатури (якщо потрібно), виводу з форматуванням даних, що виводяться. Ця програма повинна виконувати такі дії: виводити на екран повідомлення про те, для чого вона призначена, наприклад, "Programa dlia znaxodgennia sumy dvox chysel"; зчитувати дані з клавіатури; за заданими значеннями змінних провести розрахунки і вивести результат на екран.

Вимоги при захисті задачі.

1.               Студент повинен придумати і відлагодити контрольний приклад, що демонструє правильну роботу програми. Для прикладу бажано брати прості числа, що рахуються усно.

2.               Студент повинен легко орієнтуватися в програмі, на вимогу викладача вносити в неї невеликі зміни, вміти пояснити роботу операторів вводу-виводу. Наприклад, ввести прискорення з клавіатури, написати оператор, що друкує підказку для вводу і т.д.

Додаток. Розділ 1.

1.1А. Дані два дійсних числа. Знайти їх суму, різницю і добуток.

1.2А.Дано два відмінних від нуля числа. Знайти суму, різницю, добуток і частку їх квадратів.

1.3А.Дано два відмінних від нуля числа. Знайти суму, різницю, добуток і частку їх модулів.

1.4А. Дані сторони прямокутника a і b. Знайти його площу і периметр.

1.5А.Знайти площу і периметр ромба, якщо дано його діагоналі d₁ i d₂.Дано довжину ребра куба a. Знайти його об’єм і площу поверхні.

1.6А.Дані довжини ребер a, b, c прямокутного паралелепіпеда. Знайти його об’єм і площу поверхні.

1.7А. Знайти довжину кола і площу круга заданого радіуса R (=3.14).

1.8А. Дана довжина L кола. Знайти її радіус R і площу S круга, обмеженого цим колом (=3.14). 1.9А. Дана площа S круга. Знайти його діаметр D і довжину L кола, що обмежує цей круг (=3.14).

1.10А.Дані два круги зі спільним центром і радіусами R1 і R2 (R1>R2). Знайти площі цих кругів, а також площу кільця, зовнішній радіус котрого рівний R1, а внутрішній - R2.

1.11А. Дані катети прямокутного трикутника. Знайти його гіпотенузу, периметр і площу.

1.12А.Дані гіпотенуза і катет прямокутного трикутника. Знайти другий катет, радіуси вписаного і описаного кола.

1.13А.Для рівностороннього трикутника з стороною а знайти радіус вписаного і описаного кола.

1.14А. Обчислити відстань між двома точками А(x₁,y₁), B(x₂,y₂).

1.15А.Дані три точки A, B, C на числовій осі. Точка C розташована між точками A і B. Знайти добуток довжин відрізків AC і BC.

1.16А.Знайти скалярний добуток двох векторів, заданих своїми координатами на площині (у просторі).

1.17А. Дані координати двох протилежних вершин прямокутника: (x1, y1), (x2, y2).

Сторони прямокутника паралельні осям координат. Знайти периметр і площу цього прямокутника.

 

У завданнях 1.1Б – 1.10Б: x, y, z - задані дійсні числа. Написати програму, яка обчислює a, b, якщо:

a; b xarctgze^{x3} 



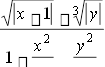
1.1Б.                 2       4                                           ;

                    a        3ey1                  ; b1y x  y x2  y x 3

                                                                                                                             2              3

1.2Б. ;

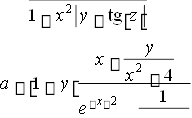 x²  ⁴ _{; b} 1x2₄ cos siny2z2_;

1.3Б.

x   2 z a y ; b1 tg 

2

1.4Б. ;

z2

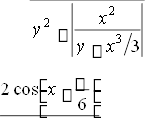a; b1

                                   sin²y          

1.5Б. ⁵ ;

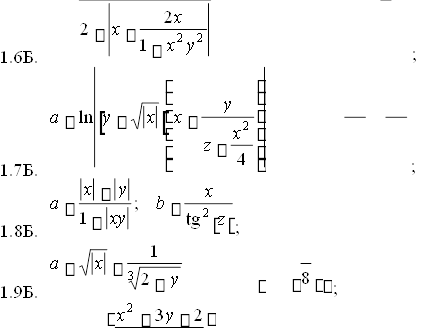a 1 sin ² x y  x; b cos₂ arctg_1__

                                                                                                                     z

                                                                                                                      x3         x5

                                                                                            ; b  x        

                                                                                                                        3      5

; b sinln2z

1.10Б. a  ln      z 1   ; b  3 x 12  5 z 13 .



1.11Б. Тіло маси m здійснює коливання на пружині з коефіцієнтом жорсткості k. Який період цих коливань?

1.12Б. Знайти час падіння каменя на поверхню Землі з висоти Н.

1.13Б. Знайти час польоту каменя, кинутого горизонтально зі швидкістю v₀ з точки на висоті Н над поверхнею Землі. На яку відстань L він переміститься по горизонталі?

1.14Б. Камінь кинули з початковою швидкістю v0 під кутом α до горизонту. Знайти час падіння каменя на Землю, максимальну висоту підйому Н і дальність польоту L.

1.15Б. Швидкість літака v = 900 км/год. Знайти швидкість літака відносно Землі при попутному і зустрічному вітрі. Швидкість вітру вводити з клавіатури.

1.16Б. Швидкість човна у стоячій воді V км/год, швидкість течії річки U км/год (U<V). Час руху човна по озеру T1 год, а по річці (проти течії) — T2 год. Знайти шлях, який пройшов човен.

1.17Б. Локомотив, перебуваючи на відстані L метрів від світлофора при швидкості 72 км/год, почав гальмувати. Чи встигне локомотив загальмувати перед світлофором, якщо він рухався з прискоренням -0.1 м/с²?

1.18Б. Швидкість першого автомобіля V1 км/год, другого — V2 км/год, відстань між ними S км. Визначити відстань між ними через T годин, якщо автомобілі віддаляються один від одного.

1.19Б. Швидкість першого автомобіля V1 км/год, другого — V2 км/год, відстань між ними S км. Визначити відстань між ними через T годин, якщо автомобілі рухаються назустріч один одному.

1.20Б. Знайти час, за який зустрінуться два тіла, що рівноприскорено рухаються назустріч одне одному, якщо відомі початкові швидкості, прискорення і початкова відстань між ними.

1.21Б. Снаряд зенітної гармати, випущений вертикально вгору зі швидкістю 800 м/с, досяг цілі через t секунд. На якій висоті знаходився ворожий літак?

1.22Б. З гармати під кутом α до горизонту вилітає снаряд зі швидкістю 800 м/с. Визначити дальність польоту снаряда. Провівши розрахунок кілька раз, визначте, для якого α дальність польоту є максимальною.

1.1С.Поміняти місцями значення змінних A і B і вивести нові значення A і B (інші змінні не використовувати).

1.2С.Дані змінні A, B, C. Змінити їх значення, перемістивши значення A в B, B — в C, C — в A, і вивести нові значення змінних A, B, C.

1.3С.Дано число A. Обчислити A¹⁵, використавши дві допоміжні змінні і п’ять операцій множення.

1.4С. Дано двозначне число. Знайти суму і добуток його цифр.

1.5С.Дано двозначне число. Вивести число, отримане при перестановці цифр вихідного числа.

1.6С. Дано тризначне число. Знайти суму і добуток його цифр.

1.7С.Дано тризначне число. В ньому закреслили першу справа цифру і приписали її зліва. Вивести отримане число.

1.8С.З початку доби пройшло N секунд (N — ціле). Знайти кількість повних хвилин і годин, що минули.

1.9С.Дні тижня пронумеровані наступним чином: 1 — понеділок, 2 — вівторок, …, 6 — субота, 7 — неділя. Дано ціле число K з проміжку 1–365. Визначити номер дня тижня для K-го дня року, якщо відомо, що в цьому році 1 січня було суботою.

Лабораторна робота 4. Алгоритми з розгалуженням (2 год.)

Зміст заняття: Використання операторів умови IF, вибору CASE для програмування алгоритмів з розгалуженням; оператор безумовного переходу.

1.Задача

1

Знайти значення функції  f (x) ₂                                        

x 3x 15

А) Теорія

Знайти значення функції можна, якщо підставити значення х у формулу для f(x), якщо вона визначена. Розрахунок значення функції можливий, якщо A = х² - 3x - 15 > 0, при A  0 функція не визначена.

Б) План

а) опис змінних x, f, A

б) ввід x

в) розрахунок A= x² - 3x – 15

г)                                     якщо A > 0

                   так :                       |                           ні :

            f = A^-1/2                           |   надрукувати ” при x = … ф-ція не визначена” 

                                                  |                                                        видрукувати значення x, f      |

                                        кінець

2. Умовний і складний оператори

Для реалізації розгалуження дій у програмі можна використовувати умовний оператор:

                    If  <умова>  then  <оператор1>                                     else  <оператор2>;

де умова – це вираз логічного типу (наприклад: а > 0; (d<0) and (c=5) – складна умова; та інше). Якщо ця умова виконується, то програма виконує гілку then, тобто оператор1, якщо умова не виконується – то оператор2.

 Якщо у якійсь гілці розгалуження програма повинна виконати не одну, а кілька дій, тобто потрібно використати кілька операторів, то ці оператори слід об’єднати у складний оператор: 

begin

<оператори> end

Тобто слід помістити їх між службовими словами begin та end, як зроблено у наведеному нижче прикладі програми. У цьому випадку послідовність операторів, об’єднана в групу всередині begin ... end розглядається як один оператор чи блок. Складний оператор використовується у тих випадках, коли за правилами мови можна використати лише один оператор, а дій треба виконати кілька. Складний оператор часто використовується при написанні операторів умови, вибору та циклу.

3. Програма

program rozgalugennia;  var     x, f, A: real; begin

 write(‘Vvedit x ’);  read(x);

 A:=sqr(x) – 3*x – 15;  if A>0 then            begin             f:=1/sqrt(A);

            writeln(‘f(‘,x:2:1,’)=’,f:5:3);           end {pered else krapka z komoju ne stavytsia,}               {adge ce wche ne kinec operatora umovy!!!}         else           writeln(‘pry x=’,x:3:1,’ f-cija ne vyznachena’);  end.

Тут складний оператор стоїть у гілці then оператора умови, і після нього оператор умови не закінчується – адже є ще гілка else, саме тому після end не ставиться крапка з комою (знак кінця оператора).

4. Скорочена форма оператора умови і оператор безумовного переходу

Вітка elseв операторі умови може бути відсутня, тоді це називається скороченою формою оператора умови: 

if <умова> then <оператор1>;

Якщо умова не виконується, то гілка then ігнорується (тобто оператор1 не виконується) і управління передається наступному після іf оператору. Також можна використовувати мітки, що позначають деякі оператори програми, необхідні програмісту. Мітка – це набір цифр чи букв, що відділяється двокрапкою від операторів, які вона мітить (див. програму нижче). У мові Паскаль прийнято перед використанням міток описувати їх, тобто перераховувати через кому у блоці описів після службового слова label. Можна організувати перехід до мітки за допомогою оператора goto m, де m - ім’я мітки. Задачу, що розглядається, можна запрограмувати по-іншому:

program rozgalugennia2;  label 1;  var

  x, f, A: real; begin

 write(‘Vveddit x ’);  read(x);

 A:=sqr(x) – 3*x – 15;  if A>0 then goto 1;

 writeln (‘pry x=’,x:2:1,’ funkcija ne vyznachena’); exit;                       {vyxid z programy}

1:   f:=1/sqrt(A);

writeln(‘x=’,x:3:1,’    f=’,f:6:3); end.

5. Оператор вибору

Якщо для розв’язку задачі необхідно організувати більше, ніж дві гілки, зручно скористатися оператором вибору CASE. Загальний вигляд оператора:

            case <селектор> of

                        значення 1: <оператор1>;                         значення 2: <оператор2>;

                        ………

                        значення N: <операторN>;                         else              <оператор>                 end;

де селектор - це змінна чи вираз цілого або символьного типу, припускається використання і деяких інших типів. Набір значень - це конкретні значення селектора, при яких буде виконано відповідно потрібний оператор. Оператор вибору працює так: спочатку обчислюється значення селектора (якщо це вираз). Потім відбувається перехід до виконання оператора, що відповідає отриманому (чи текучому) значенню селектора. Якщо ж значення селектора не співпало з жодним з вказаних, то виконується гілка else. Тоді нашу задачу можна написати так:

program rozgalugennia3;  var

  x, f, A, n : real; begin

 write(‘vvedit x’);  read(x);

 A:=sqr(x) – 3*x – 15;  n:=A/(abs(A)+1); 

case  round(n)  of   {selektor povunen buty cilogo typu}

     -1:   writeln(‘ funkcija ne vyznachena’);

      1:   begin              f:=1/sqrt(A);

             writeln(‘x=’,x:4:1,’    f=’,f:6:3);           end;

    end;                     {kinec operatora vyboru} end.

6. Самостійна робота

Кожен студент отримує задачу з розділу 2 додатку. 

Вимоги при захисті задачі.

1.               Повинна бути написана і відлагоджена програма, що містить оператори присвоєння, вводу з клавіатури (якщо потрібно), вивід з форматуванням, оператор IF (чи CASE). Студент повинен придумати і відлагодити контрольний приклад, що демонструє правильну роботу усіх гілок програми.

2.               Студент повинен легко орієнтуватися в програмі, вміти обгрунтувати вибір використаних операторів або запропонувати еквівалентний, знати їх роботу.

Додаток. Розділ 2.

2.1А. Дані числа X, Y, Z. Надрукувати ті з них, що менші нуля.

2.2А. Дані числа X, Y, Z. Вибрати з них максимальне, мінімальне і середнє.

2.3А. З’ясувати, чи існує прямокутний трикутник зі сторонами X, Y, Z. Якщо так, знайти його площу.

2.4А. Визначити тип трикутника з довжинами сторін X, Y, Z (прямокутний, гострокутний чи тупокутний).

2.1Б. Написати програму для розрахунку коренів квадратного рівняння ax²+bx+c=0, яка би виводила кількість коренів (2, 1 чи дійсних нема) і їх значення. Ввідні дані - коефіцієнти рівняння.

2.2Б. Визначити, яка з точок A(X₁,Y₁) чи B(X₂,Y₂), розташована ближче до початку координат.

2.3Б. Дано натуральне число N (N<13), що позначає місяць у високосному році. Додати до цього числа відповідне число днів: «29», «30», «31». 

2.4Б. Снаряд вилітає з гармати зі швидкістю V = 300 м/с під кутом  до горизонту. Ціль знаходиться на відстані S метрів. Програма має визначити, чи попав снаряд в ціль (тобто впав на відстані, меншій за 5 метрів від неї), чи був недоліт чи переліт.

2.5Б. Дані числа a, b, c, d. З’ясувати, чи можна прямокутник зі сторонами а, b вмістити всередині прямокутника зі сторонами c, d.

2.6Б. З’ясувати, чи пройде цеглина з ребрами a, b, c у прямокутний отвір розміром x, y.

2.7Б. Дано натуральне число N (N<100), що позначає вік людини у роках. Додати до цього числа відповідне слово: «років», «рік», «роки».

2.8Б. У кіоску продається газета вартістю 1 грн. і журнал за 10 грн. Скласти програму, що запитує користувача про кількість газет та журналів, які він бажає придбати, приймає гроші (сума вводиться з клавіатури) і друкує решту, що належить клієнту.

2.9Б. Визначити, чи лежить точка A(X,Y) на прямій Y = 2x+3. Якщо так, то знайти квадрат відстані від цієї точки до початку координат. Інакше знайти рівняння прямої, що проходить через цю точку паралельно до даної прямої.

2.10Б. Визначити, чи лежить точка A (координати ввести з клавіатури) на прямій Y = 4x-3, вище чи нижче цієї прямої.

2.11Б. З’ясувати, ззовні, всередині чи на колі з центром С (3,4) і радіусом R=5 лежить точка, координати якої вводяться з клавіатури.

2.12Б. Задано дві прямі в декартових координатах y = a₁x+b₁ , y = a₂x+b₂. Написати програму, що виводить координати точки перетину, якщо прямі перетинаються, чи повідомлення, що ці прямі параллельні. Вхідні дані - коефіцієнти рівнянь.

2.13Б. Задано пряму і коло в декартових координатах: y = a₁x+b₁, R² = y²+x². Написати програму, що виводить координати точок перетину, чи точки дотику, чи повідомлення, що вони не перетинаються. Вхідні дані - коефіцієнти рівнянь.

2.14Б. Задано два кола в декартових координатах: R₁² = (y+a₁)² + (x+b)² , R₂² = (y+a₂)² +

(x+b)². Написати програму, що виводить координати точок перетину, чи точки дотику, чи повідомлення, що вони не перетинаються. Вхідні дані - коефіцієнти рівнянь.

2.1С. Лід масою m=1 кг нагрівають від температури Т₁ до температури Т₂. Програма має визначати кількість теплоти, яку треба затратити на цей процес, якщо температура Т₂ може бути більша, рівна чи менша 0^о. Питома теплоємність льоду 2100 Дж/кгград, води 4200 Дж/кгград; питома теплота плавлення льоду q=334 кДж/кг.

Лабораторна робота 5. Циклічні алгоритми. Табулювання функцій (2 год.)

Зміст заняття: Використання операторів циклу FOR, REPEAT, WHILE для табулювання функцій і розрахунку сум.

1.Задача.

Протабулювати функцію f(x) = x³ e^{Sin x} для x [1, 10].

А) Модель

В таких задачах необхідно знайти ряд значень функції f для ряду значень аргумента x, які відрізняються між собою на однакову величину (крок) і вивести таблицю значень аргумента і розрахованих значень функції (це називається протабулювати функцію з певним кроком).

Позначимо граничні значення аргумента x₀ = 1 і x_k = 10. Виберемо крок h = 1, тоді всього у таблиці буде i_k = (x_k - x₀)/h+1=10 стрічок. Позначимо лічильник стрічок таблиці i, тоді значення аргумента в i-тій стрічці можна розрахувати за формулою x_i = x₀ + h*i, тобто x_i

= 1 + 1*i, де i = 0i_к (цей запис означає, що i змінюється від 0 до i_к). Для кожного x_i можна розрахувати значення функції f(x_i).

Б) План

а) описати змінні x, x₀, h, x_к, i, f;

б) ввести x₀, h, x_к;

в) роздрукувати назву таблиці, надрукувати перший рядок – х₀, f(х₀);

г) розрахувати x₁, f(x₁); надрукувати x₁, f(x₁); розрахувати x₂, f(x₂); надрукувати x₂, f(x₂); і так далі, поки x_i  x_к.

Останні пункти плану (ряд однотипних дій) можна запрограмувати з допомогою циклічних структур, передбачених у мові Паскаль.

2. Види операторів циклів

1) Цикл з лічильником

           Загальний вигляд оператора:

           For <лічильник>:=<почзнач> To <кінцзнач> Do <оператор>,

де лічильник циклу (його ще іноді називають параметр) повинен бути одного з наступних типів: цілого, символьного, логічного чи перерахункового. Того ж типу повинні бути початкове (почзнач) і кінцеве (кінцзнач) значення лічильника циклу, які можуть бути виразами, змінними чи константами. У цьому циклі лічильник збільшується на мінімальне значення (для цілого типу – на одиницю). Часто в циклі необхідно повторити не один, а кілька операторів. Пригадаємо собі, що тоді у якості оператора слід використовувати послідовність операторів, об’єднану службовими словами begin і end, тобто складний оператор.

Послідовність виконання оператора for 

Змінній - лічильнику циклу  присвоюється вказане початкове значення, потім перевіряється умова, чи не перевищує лічильник циклу вказане кінцеве значення. Якщо це так, оператор for закінчує свою работу. У протилежному випадку виконується вказаний <оператор>, після чого значення параметра циклу збільшується на одиницю, і цикл повторюється. Якщо початкове значення більше за кінцеве, цикл не виконається жодного разу.

1.   Обчислюються початкове і кінцеве значення лічильника і фіксуються;

2.   Якщо почзнач <= кінцзнач, то виконується оператор;

3.   Якщо значення лічильника  кінцзнач, то значення лічильника циклу зростає (для цілого – на одиницю).

4.   Виконується оператор, перехід до п.3

5.   Цикл виконується останній раз, коли значення лічильника = кінцзнач, потім управління передається оператору наступному після оператора циклу.

В операторі for замість слова to може стояти слово downto: for <лічильник>:=<кінцзнач> downto <почзнач> do <оператор>

В такому випадку при кожному проходженні циклу значення лічильника буде зменшуватися на одиницю. Очевидно, тут почзнач повинно перевищувати кінцзнач або дорівнювати йому, інакше цикл не буде виконуватися.

 

2) Цикл з передумовою

Якщо у задачі кількість повторів наперед невідома, цикл for використовувати незручно і можна скористатись оператором (загальний вигляд):

                              While  умова DO <оператор>,

де умова – логічний вираз, оператор може бути простим чи складним. Порядок виконання оператора

Спочатку перевіряється умова (тому і цикл - з ПЕРЕДумовою): якщо вона виконується (істинна), то виконується оператор. Потім знову перевіряється умова і т.д., поки умова не перестане виконуватися, тобто не виконання умови є причиною виходу з циклу. Якщо умова не виконується (невірна), то оператор ігнорується і управління передається наступному за циклом оператору.

3) Цикл з післяумовою Загальний вигляд оператора:

  Repeat

          <Оператор 1>;

          <Оператор 2>;

             …

          <Оператор N>;

  Until умова; Порядок виконання оператора:

Виконання операторів від 1 до N повторюється, поки умова не почне виконуватися (не стане істинною), тобто виконання умови є причиною виходу з циклу. Таким чином, оператор repeat  until завжди виконається принаймі один раз. 

 

Кожен з цих циклів може бути використаний для програмування поставленої задачі. Нижче приведені три програми, кожна з яких використовує свій вид циклу дл я розв’язання нашої задачі.

3. Застосування циклу з лічильником

program cikl1; var

    x0, xk, x, h, f: real;

    ik, i: integer;  begin

   write('Vvedit x0,xk,h  ');    read(x0, xk, h);    ik:=trunc((xk-x0)/h);    writeln('Tabuliuvannia funkciji');    writeln('____________');    writeln('|    x   |      f     |' );    writeln('___________');      for i:=0 to ik do         begin           x:=x0 + i*h;

          f:= exp(3*ln(x))*exp(Sin(x));           writeln(' | ',x:5:1,' | ',f:10:3,' | ');         end;    writeln('___________'); end.

У цій програмі враховано, що у мові Результат виконання програми: Паскаль немає операції піднесення Vvedit x0,xk,h  1 10 1 до степеня, тому х³ = exp(3 ln(x)). Tabuliuvannia funkciji Ввід трьох значень в операторі _______________

read(x0, xk, h) відбувається через |     x    |           f     | пробіл. Оскільки за правилами мови _______________ Паскаль цілій змінній ik можна  |    1.0 |       2.320 | присвоїти лише ціле значення, для  |    2.0 |     19.861 | отримання       такого         значення  |    3.0 |     31.092 | використовується функція trunc(..),  |    4.0 |     30.027 | що відкидає дробову частину числа,  |    5.0 |     47.913 | отриманого після          виконання   дій  |    6.0 |     63.345 |

(xk-x0)/h.  |    7.0 |   661.637 |

  |    8.0 | 1377.028 |

 |    9.0 | 1100.800 |

 |  10.0 |   580.410 |

       _______________

4. Застосування циклу з передумовою

program cikl2; var

  x, x0, xk, h,f: real; begin

  write('Vvedit x0, xk,h  ');   read(x0, xk, h);

  writeln(‘Tabuliuvannia funkciji');   writeln('________________________');   writeln('|   x   |      f       |' );   writeln('________________________');   x:= x0;

  while x <= xk do {operator pislia do vykonujetsia}     begin         {poky umova x <= xk  vykonujetsia}       f:=exp(3*ln(x))*exp(Sin(x));{tut operatorom je}       x:= x + h;        {skladnyl operator begin...end}       writeln(' | ',x:5:1,' | ',f:10:3,' | ');

    end;

  writeln('________________________'); end.

5. Застосування циклу з післяумовою

program cikl3; var

  x, x0, xk, h,f : real; begin

  write('VVedit x0,xk,h   ');   read(x0, xk, h);

  writeln('Тabuliuvannia funkciji');   writeln('________________________');   writeln('|   x  |   f        |' );   writeln('________________________');   x:= x0;

  repeat    {operatory mig repeat i until vykonujytsia}             {poky umova x>xk ne stane istynnoju}      f:=exp(3*ln(x))*exp(Sin(x));

     writeln(' | ',x:5:1,' | ',f:10:3,' | ');      x:= x + h;   until x>xk;

  writeln('________________________'); end.

6. Самостійна робота

Кожен студент отримує задачу з розділу 3 додатку.

 

Вимоги при захисті задачі

1.               Повинна бути написана і відлагоджена програма, що містить оператори присвоєння, вводу з клавіатури (якщо потрібно), вивід з форматуванням у вигляді таблички, оператори циклу FOR, WHILE чи REPEATE.

2.               Студент повинен легко орієнтуватися в програмі, на вимогу викладача вносити в неї невеликі зміни, наприклад, вміти замінити цикл з передумовою на цикл з після умовою і т.д., а також вміти обґрунтувати вибір оператора циклу в залежності від умов, сформульованих викладачем.

Додаток. Розділ 3.

У завданнях 3.1.- 3.25 потрібно протабулювати функцію ^{f x} на заданому відрізку ^a,b з кроком h. Знайдені значення мають виводитися (вивід повинен бути форматований!) на екран у вигляді таблиці.

                                        x x² 1cosx           ^ex 2^x

3.1A. y(x) = , крок 0,05, х = 1..15

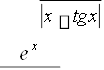                                      (x  5)²               ln(x² 1)

3.2A. Y(x) =                     x ^ tgx                     , крок 0,007, х = 1..2

x3 x2 _1_33x _ e^x

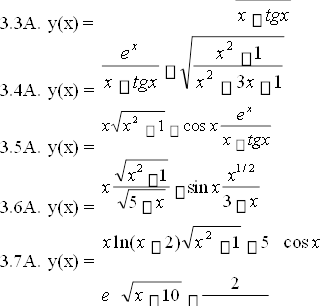
, крок 0,06, х = 1..10

 arctgx

, крок 0,001, х = 2..3

, крок 0,002, х = 3..3,5

, крок 0,005, х = 0..1 x      10

x sin ^x , крок 0,05, х = 0,5..10

x

3.8A. y(x) =                       5  sin ^x , крок 0,003, х = 2..3

                                               1             e3x

^{3 34}^{6x x  5} 10x ex x

3.9A. y(x) =                      ^{3 10} , крок 0,04, х = 0,1..5

3.10A.          y(x) =                       12cos^x , крок 0,04, х = 1..10

3x

                                                             1          tg(x  2)       x

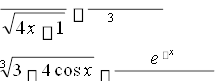 2

3.13A.          y(x) =                      ^{x 10}           , крок 0,005, х = 4..5

 tg(x 5)

3.14A.          y(x) =                          x²  2x ¹⁰                   , крок 0,01, х = 1..4

3.15A.         y(x) = 4 sinx cosx  x3e310x , крок 0,002, х = 0,1..0,5

                                                              3                               33x

x

 , крок 0,025, х = 3..10

3.1Б. Отримати таблицю температур по Цельсію від 0 до 100 і їх еквівалентів по шкалі Фаренгейта і по шкалі Реомюра, користуючись формулами: T_F = 1,4T₀+32, T_R = 0,8T₀. 3.2Б.Надрукувати таблицю відповідності між вагою у фунтах і вагою в кілограмах для значень від 1 до 10 фунтів з кроком 1 фунт (1 фунт = 400 г). 

3.3Б. Надрукувати таблицю переводу відстаней в дюймах у сантиметри (1 дюйм =2.54 см) для значень від 1 до 10 дюймів з кроком 1 дюйм.

3.4Б. Роздрукувати таблицю переводу відстаней в метрах у ангстреми (1Å = 10^-10м) для значень від 0 до 10^-9 метрів (крок 0,5∙10^-10 м).

3.5Б.          Написати програму, що роздруковує таблицю переводу кутів в радіанах у градуси (π радіан = 180 градусів) для значень від 1 до 10 радіан з кроком 0,5 радіан.

3.6Б. Написати програму, котра роздруковує таблицю перетворення відстаней у світлових роках (відстань, яку світло проходить за 1 рік) в кілометри для значень від 1 до 10 світлових років (крок 0.5 св.р.).

3.7Б. Роздрукувати таблицю перетворення сили у Ньютонах в дини (1 дина СГС=10⁵ Н) для значень від 1 до 100 Н з кроком 2 Н.

3.8Б. Написати програму, що роздруковує таблицю переводу тиску в мм.рт.ст. в Паскалі (1 мм.рт.ст. = 1.333∙10^-3 Па) для значень від 650 до 750 мм.рт.ст. з кроком 10 мм.рт.ст.

3.9Б. Роздрукувати таблицю перетворення об’єму в сантиметрах кубічних (від 1000 до 2000 см³ з кроком 50) у метри кубічні та літри.

3.10Б. Написати програму, що роздруковує таблицю переводу потужності у кінських силах в кіловати (1 кВт =1.36 к.с.) для значень від 40 до 100 к.с. з кроком 10 к.с.

3.11Б. Написати програму, що роздруковує таблицю перетворення відстаней в метрах (від 1 до 100 м, з кроком 10 м) у кілометри і в сантиметри.

3.12Б. Світло при падінні на металеву поверхню може вибити з неї електрони, котрі вилітають зі швидкістю V. Електрон вилітає, якщо енергія падаючого кванта перевищує meV 2

роботу виходу даного металу hA. Написати програму, що роздруковує

2

таблицю залежності швидкості електрона, що вилетів з міді (А = 4.4 еВ), від довжини хвилі падаючого світла  для значень від 200 до 500 нм з кроком 30 нм.

3.13Б. Написати програму, котра роздруковує таблицю залежності положення тіла від часу, якщо воно падає з висоти H з початковою швидкістю V0.

3.14Б. Густина повітря зменшується з висотою h за законом: ₀e^zh . Вважаючи, що

₀= 1.29 кг/м³, z=1.25*10^-4 1/м, надрукувати таблицю залежності (h) для значень від 0 до 1000 м, з кроком 100 м.

3.15Б. Камінь масою 200 г кинули під кутом  до горизонту зі швидкістю 20 м/c. Побудувати таблицю залежності координат каменя від часу.

3.16Б. Камінь масою 200 г кинули під кутом  до горизонту зі швидкістю 20 м/c. Побудувати таблицю залежності дальності польоту і максимальної висоти підйому каменя від кута .

3.17Б. Отримати таблицю залежності кута заломлення β від кута падіння , якщо світловий промінь падає на межу поділу двох середовищ з показниками заломлення n₁= 1.33 (вода), n₂= 1.

3.18Б. Протабулювати функцію f (x)  x²  x 6. Програма також має визначити, скільки раз функція змінює знак у заданому проміжку (використовуйте добуток значень функції у сусідніх точках).

3.19Б. Протабулювати функцію f (x)  x /2 sin(x) . Програма також має визначити, скільки раз функція змінює знак у заданому проміжку (використовуйте добуток значень функції у сусідніх точках).

3.20Б. Протабулювати функцію f (x)  x²  x 6. Програма також має визначити, скільки раз функція змінює знак у заданому проміжку (використовуйте добуток значень функції у сусідніх точках).

3.1С. Вводиться послідовність з N цілих чисел. Знайти суму всіх від’ємних чисел.

3.2С. Вводиться послідовність з N цілих чисел. З’ясувати скільки в ній нулів.

3.3С. Вводиться послідовність з N цілих чисел. Знайти найбільше число.

3.4С. Вводиться послідовність з N цілих чисел. Знайти найбільше з усіх від’ємних чисел.

3.5С. Вводиться послідовність цілих чисел, 0 – кінець послідовності. Знайти два найменші числа.

3.6С. Вводиться послідовність цілих чисел, 0 – кінець послідовності. З’ясувати, чи містить послідовність принаймі два послідовних елементи, що рівні між собою.

3.7С. Вводиться послідовність цілих чисел, 0 – кінець послідовності. З’ясувати, скільки разів послідовність змінює знак.

 

 

Лабораторна робота 6. Ряди. (2 год.)

Зміст заняття: Використання операторів циклу для розрахунку сум та послідовностей.

1. Задача

З точністю 10^-6 розрахувати суму ряду S 1_+... 

2. Теорія

Для того, щоб знайти шукану суму, пронумеруємо доданки ряду:  i = 1,   2,  3,…  -номер доданка. Тоді можна вивести формулу для розрахунку i-го члена такого знакозмінного ряду: _сi _ ^(1)i^{i 1} , тоді шукана сума запишеться як _S i^_1_ci , тут c₁ =1,   c₂ = -1/2 і т.д. Цей ряд є безконечним, а комп’ютер може сумувати лише скінчену кількість доданків. У цьому випадку можна або заздалегідь вибрати число доданків N, або (як це вимагається у даній задачі) сумувати члени ряду до досягнення заданої точності. Вважається, що потрібна точність досягнута, якщо черговий доданок | с_i | < =10^-6. Така задача знаходження суми ряду з заданою точністю може бути запрограмована з допомогою циклів з перед- чи післяумовою. У наведеній програмі  позначена як eps, змінна z містить знак чергового доданка.

3.   Програма program Summa; var

 s, c, eps, z, i: real; begin

write(’vvedit tochnist ’);  read(eps);  s:=0;  z:=1;  i:=1;  repeat    c:= z/i;   s:=s+c;   z:=-z;   i:=i+1;  until abs(c) < eps;

 writeln(‘shukana suma s= ’,s:10:6);  writeln(‘prosumovano ’,(i-1):3:0,’ dodankiv’); end.  

4.   Самостійна робота

Кожен студент отримує задачу з розділу 4.

Вимоги при захисті задачі

1.               Повинна бути написана і відлагоджена програма, що містить оператори присвоєння, вводу з клавіатури (якщо потрібно), вивід з форматуванням, один з операторів циклу.

2.               Студент повинен легко орієнтуватися в програмі, на вимогу викладача вносити в неї невеликі зміни, наприклад, вміти замінити цикл з передумовою на цикл з після умовою і т.д., а також вміти обґрунтувати вибір оператора циклу в залежності від умов, сформульованих викладачем.

 

 

 

Додаток. Розділ 4.

4.1А. Знайти суму всіх натуральних чисел від 0 до N і їх середнє арифметичне. Суму порівняти зі значенням, обчисленим за формулою S=N(N+1)/2.

4.2А. Знайти суму квадратів перших N натуральних чисел і їх середнє арифметичне.

4.3А. Знайти суму квадратів перших N непарних чисел і їх середнє арифметичне.

4.4А. Знайти суму перших N членів арифметичної прогресії:   a₁=1, b=5, a_k+1 = b + a_k.

4.5А. Знайти суму перших N членів геометричної прогресії:  a₁=1, b=2, a_k+1 = b*a_k.

4.6А. Розрахувати суму рядів: (n -     задане натуральне число, x -  задане дійсне число).

4.7А.  K             ¹               

                sin1 sin1 sin2 sin1K sinn

                   1         1                            1

4.8А.      K  x xx 1 xx 1Kx  n

                        1      1       1              1

4.9А. x 2  x4 K x₂n

x

4.10А. sinx sin²xK sinⁿx

Знайти безконечну суму з точністю . Порівняти результат наближених обрахунків зі значеннями, отриманими з допомогою стандартних функцій мови Turbo Pascal (використовувати тип extended).

                                                  x2             x4 x6

4.1Б.cosx1   K ; 2! 4! 6! x3 x5 4.2Б.sinx x    ;  3! 5! x3 x5

4.3Б. arctgx    x             ;                          для x 1

                                                     3     5

                      ^x           1x x2  x3 K ;

4.4Б. e 

                                                   2!     3!

                      ^x      1    x  x2  x3      ;

4.5Б. e   2! 3!

                   1     1     1     1     1

4.6Б.                       K

                   e    2!   3!    4!   5!

4.7Б. ln x _ xx^1 _ x2^x1₂²  x₃^_x1₃³        ,   для x _ 1₂;

                                                        x2             x3 x4

4.8Б. ln1xx   K ;

                                                         2      3      4

4.9Б. ^1 1  1  1 K ;

4 3 5 7

2 1 1 1

4.10Б.             6 1 2 ₃2 ₄2 K ;

₂

                                   2                   1      1      1

4.11Б.            12 1 2 ₃2 ₄2 K ;

₂

                       2                   1      1      1

4.12Б.          8 1 2  ₅2  ₇2 K ;

₃

4.13Б.   1 x 1   x    x²    x³    x⁴ ...

                                         ex ex                  x3        x5

4.14Б. sh x    x              ;

                                                2              3!    5!

                                        e +ex x                    x2 x4

4.15Б.  ch x    1            ;

2            2!   4! x    1 x³       1 3 x⁵  1 3 5 x⁷

4.16Б.  arcsin x  arctg x                                            , x 1;

                                                                  1 x²                  2   3      2 4    5       2 4 6     7

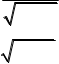
4.17Б.  arsh x  lnx  1 x²   x _ 1 _ x³ _ 1 3_{ } x⁵ _ 1 3 5_                 _ x⁷ _ , x 1;

                                                                                                  2   3      2 4    5      2 4 6     7

                                        ^m                      m m^ 1^{ 2} m m^ 1^m 2^x³  , для |x|<1, m – будь-яке

4.18Б. 1 x_  1 mx              x 

                                                                           1 2                  1 2 3      

дійсне число.

4.19Б. 1 x_^m _{  }1 mx m m^{ }1^ x² _ m m^{ }1^m^ 2^ x³  , m – натуральне.

                                                                               2!                        3!

4.20Б. Скласти програму обчислення чисел Фібоначчі за рекурентною формулою: F₀=1, F₁=1, F_n+1=F_n+F_n-1. Золотий переріз, що використовується у архітектурі, визначається за формулою V_n=F_n/F_n-1. Розрахувати його і порівняти з точним значенням 1.618.

4.21Б. Дано ціле число N (> 1), що є числом Фібоначчі: N = F_K. Знайти цілі числа F_K–1 і F_K+1 - попереднє і наступне числа Фібоначчі.

4.22Б. Дано ціле число N (> 1), що є числом Фібоначчі: N = F_K. Знайти ціле число K – його порядковий номер.

4.23Б. Дано дійсне число  (> 0). Послідовність дійсних чисел A_K визначається так: A₁ = 2,    A_K = 2 + 1/A_K–1,  K = 2, 3, … . Знайти перший з номерів K, для яких виконується умова |A_K – A_K–1| < , і вивести цей номер, а також числа A_K–1 і A_K.

4.24Б. Дано дійсне число  (> 0). Послідовність дійсних чисел A_K визначається так: A₁ = 1,    A₂ = 2,    A_K = (A_K–2 + 2·A_K–1)/3,  K = 3, 4, … . Знайти перший з номерів K, для яких виконується умова |A_K – A_K–1| < , і вивести цей номер, а також числа A_K–1 і A_K.

4.1С. Знайти потенціал електричного поля, створеного в точці А лінійним ланцюжком з M різнойменних зарядів. Відстань між зарядами L=1, між точкою А і найближчим зарядом – N. Значення M і N ввести з клавіатури. q_i /r_i , r_i- відстань від точки A до i-го заряду.

4.2С. Спортсмен-лижник почав тренування, пробігши у перший день 10 км. Кожен наступний день він збільшував довжину пробігу на P відсотків від пробігу попереднього дня (P - дійсне, 0 < P < 50). За заданим P визначити, після якого дня сумарний пробіг лижника за всі дні перевищить 200 км, і вивести знайдену кількість дней K (ціле) і сумарний пробіг S (дійсне число).

4.3С. Дані додатні числа A, B, C. На прямокутнику розміром A  B розташовано максимально можлива кількість квадратів зі стороною C, які не накладаються. Знайти кількість квадратів, розташованих на прямокутнику, не використовуючи операції множення і ділення.