Зразки розв’язування завдань. Нерівності і системи нерівностей

Зразки розв’язування завдань.

Нерівності і системи нерівностей

1.  Розв’язати нерівність .

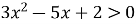Розв’язання:

Прирівняємо дану нерівність до нуля і розв’яжемо її.

Оскільки дана нерівність є квадратною, графіком якої є парабола, повернена вітками вгору, то розв’язками будуть проміжки .

2. Розв’язати нерівність .

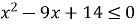Розв’язання:

Прирівняємо дану нерівність до нуля і розв’яжемо її.

Оскільки дана нерівність є квадратною, графіком якої є парабола, повернена вітками вгору, то розв’язками будуть проміжок .

3.  Розв’язати нерівність

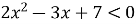
Розв’язання:

Прирівняємо дану нерівність до нуля і розв’яжемо її.

Оскільки дискримінант даного рівняння менший нуля, а парабола, яка є графіком , повернена вітками вгору то графік розташований у верхній півплощині, а нерівність розв’язку не має.

4. Розв’язати нерівність .

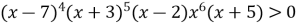Розв’язання:

Прирівняємо дану нерівність до нуля і розв’яжемо її.

      –     +              –              –            +            +

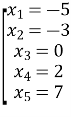
                 -5                        -3                       0                         2                      7

Відповідь: .

5.  Розв’язати нерівність .

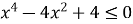Розв’язання:

Прирівняємо дану нерівність до нуля і розв’яжемо її.

Введемо заміну

Відповідь: .

6.  Розв’язати нерівність  .

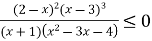Розв’язання:

          +                              +                                 +                             –                         +

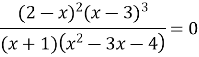
                         -1                                   2                               3                          4

Відповідь:

7.  Розв’язати нерівність  .

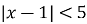Розв’язання:

Розглянемо два випадки

Відповідь: .

8.  Знайти область визначення функції .

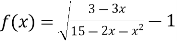Розв’язання:

Щоб знайти область визначення функції, розглянемо нерівність

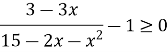
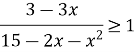
Відповідь:

9.  Розв’язати нерівність .

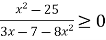Розв’язання:

Розглянемо  два випадки

І випадок:

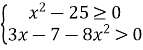
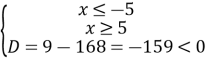
Ø

ІІ випадок:

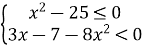
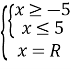
Відповідь: .

10.                    Розв’язати нерівність

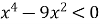
Розв’язання:

Введемо заміну

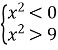
Ø

 або

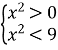
Відповідь: .