"Зростання і спадання функції"

Про матеріал

Підручник Математика Істер О.С., 2018 рік. Конспект уроку під час дистанційного навчання з самостійною роботою.

Перегляд файлу

Алгебра 10клас

Тема: Ознаки сталості. Зростання та спадання функції урок №2

Очікувані результати:

- ознайомитись з правилами знаходження критичних точок,

зростання та спадання функції.

- навчитись розв’язують завдання, застосовувати похідну

для знаходження зростання та спадання функції

Продовжимо вивчати

ознаки сталості

Для цього

потрібно

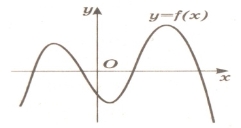
1.На рисунку зображено графік функції у = f(x), яка визначена на проміжку (-). Скільки критичних точок має ця функція? (1 бал)

$C:\Documents and Settings\Admin\Рабочий стол\цвет.jpg$

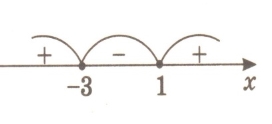
2. Знак похідної функції у = f(x), яка визначена на проміжку (-), змінюється за схемою, зображеною на рисунку (– 3 і 1 – критичні точки). Знайдіть проміжки зростання функції. (1 бал)

$C:\Documents and Settings\Admin\Рабочий стол\цвет 002.jpg$

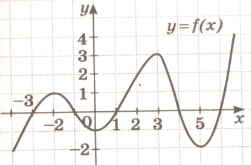
3. Укажіть критичні точки функції у = f(x)

(1 бал)

$C:\Documents and Settings\Admin\Рабочий стол\цвет 001.jpg$

4. Знайдіть точки зростання та спадання функції у = f(x) (1 бали)

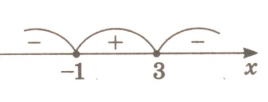
5. Знак похідної функції у = f(x), яка визначена на проміжку (-), змінюється за схемою, зображеною на рисунку (– 1 і 3 – критичні точки). Знайдіть точки зростання та спадання функції. (1 бал)

$C:\Documents and Settings\Admin\Рабочий стол\Копия цвет 002.jpg$

6. Знайдіть проміжки зростання і спадання функції у = х² – 6 (2 бали)

7. Знайдіть проміжки зростання і спадання функції у = х² – 3х + 2 на проміжку [0; 4] (2 бали)

8. Знайдіть проміжки зростання і спадання функції f(x) = х²– 3х

(3 бали) 4 - х

Самостійна робота (№ 1 – 5 писати лише відповідь, можна в таблиці)

docx

Завантажити

Зберегти на потім

Додав(-ла)

Дикун Наталя Григорівна

Пов’язані теми

Алгебра, 10 клас, Розробки уроків

Додано

30 січня 2022

Переглядів

911

Оцінка розробки

Відгуки відсутні