10 клас. Розв’язування ірраціональних рівнянь різними методами.
Тема. Розв’язування ірраціональних рівнянь різними методами
Мета уроку: Познайомити учнів з методами розв’язування ірраціональних рівнянь. Сформувати уміння розв’язувати ірраціональні рівняння різними методами ;провести корекцію знань раніше вивченого матеріалу й умінь учнів; розвивати способи й прийоми раціонального мислення, індивідуальні здібності учнів, їх пізнавальні інтереси; навички колективної та групової роботи; уміння використовувати сформовані знання, навички й уміння у видозмінених умовах; сприяти формуванню культури усного та писемного мовлення та міжособистісного спілкування.
Тип уроку: Первинне формування умінь та навичок з теми; комбінований .
Обладнання: мультимедійний проектор, робочий зошит учня, підручники, комп'ютерна презентація, інтерактивні завдання, розроблені в додатку learningapps, сайту «На урок»; Classroom; GeoGebra.
Структура уроку
І. Організаційний момент. Перевірка домашнього завдання.
Перевірка готовності учнів до уроку, відмітка присутніх (відсутніх), налаштування на роботу. На партах для кожного учня приготовлені робочі зошити з друкованою основою.
ІІ. Мотивація навчальної діяльності й цілепокладання.
Учитель. Добрий день. Я хочу розпочати наш урок із музики. Нехай вона надихне вас на роботу. (учні прослуховують музичний фрагмент) Хто автор композиції ? Підказка - коли композитор писав цю музику, він був глухим.
(Людвіг ван Бетховен, « Ода к радости»1793р.)
Як же він зміг писати музику? Композитор стверджував, що бачить картину й прямує за її лініями. «Музикант відчуває математику, а математик думає музикою», – говорив він. Бетховена називали композитором перемоги , тож і я вам бажаю тільки перемог. Оскільки досягти успіху можна тільки тоді, коли є певна мета, тож і ми озвучмо мету нашого уроку, посилаючись на тему уроку:
- Згадати, що таке ірраціональні рівняння.
- Згадати, як їх розв’язувати.
- Ознайомитися з різними методами розв’язання таких рівнянь.
- Проаналізувати, які з них найбільш зручні для конкретного рівняння.
Учитель. Я пропоную вам такий алгоритм роботи… Які ще види роботи були б цікаві вам? (відповіді учнів)
Учитель. Але спочатку перевіримо засвоєння вами матеріалу, вивченого на попередньому уроці. Бачу, що ви добре підготувалися вдома. Ваша оцінка за домашню роботу на сайті «На урок». Щоправда, дехто припустився помилки при виконанні завдання… Тож скоректуймо наші знання. Як правильно треба було розв’язати рівняння …
Перенесемо вираз (х+1) до правої частини рівняння
У рівнянні є подібні доданки,їх зводять.
Щоб звільнитися від кореня ,обидві частини рівняння підносять до квадрата: 
Зведемо подібні доданки:
Розв’яжемо,утворене квадратне рівняння через теорему Вієта 
;
Зробємо перевірку,підставляючи знайдені корені у дане
рівняння. Перевірка: 
Рівність невірна,тому -2 не є коренем даного рівняння.
-2 називають стороннім коренем даного рівняння. Підставляємо другий корень: 
; 
;
; 2=2
Відповідь: х = 1
ІІІ. Актуалізація опорних знань.
Учитель. Повторімо ті поняття, що ми вже засвоїли з теми «Розв’язування найпростіших ірраціональних рівнянь», і які нам будуть потрібні сьогодні на уроці. Увага на екран.( один з учнів виконує завдання біля дошки)
Завдання 1. Знайдіть, будь ласка, серед запропонованих рівнянь ірраціональні (слайд): https://learningapps.org/display?v=p0hskcv5320
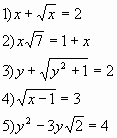
Завдання 2. Знайдіть корені рівняння: https://learningapps.org/15123273
1) 
(81)
2) 
(0).
3) 
(коренів немає )
4)
(83)
III. Опрацювання нового матеріалу.
Учитель. Молодці! Ви впорались із цим завданням. Скажіть, чи може тема «Ірраціональні рівняння» обмежитися розв’язуванням найпростіших рівнянь? Ні. Як ви вважаєте , яка мета нашого уроку? Логічно. Тож сьогодні ми й спробуємо ознайомитися з різними методами розв’язування рівнянь.
Відповідно до кількості можливих методів розв’язування таких рівнянь я об’єднала вас у чотири групи, кожна отримала випереджальне завдання: виробити алгоритми розв’язування ірраціональних рівнянь в залежності від методу, знаходити підказки в рівняннях для вибору методу розв’язування. І сьогодні ви маєте презентувати ваші наробки.
Один учень з групи представляє презентацію із складанням алгоритму розв’язання рівняння за допомогою певного методу.
Теми проектів :
1.Метод піднесення обох частин рівняння до одного степеня.( Якщо обидві частини рівняння піднести до непарного степеня, то отримаємо рівняння, рівносильне даному. При піднесенні обох частин рівняння до парного степеня отримаємо рівняння, яке є наслідком даного.) 
Розв'язання. Схема обчислень таких прикладів наступна:
Переносимо від'ємний доданок за знак рівності й підносимо корені до квадрата. Щоб не виникла ситуація, коли під коренем отримаємо від'ємне значення. У кінці обов'язково перевіряємо відповідь, або знаходимо ОДЗ ,але це приводить до громіздких записів, витрачається багато часу на розв’язання.
Оскільки підкореневий вираз повинен бути додатним, то модулі опускаємо й групуємо подібні доданки:
Отримане квадратне рівняння за теоремою Вієта має корені x=1; x=5.
Спробуймо підставити одиницю в рівняння
Отримали корені з від'ємних чисел. Це в ірраціональних рівняннях недопустимо.
Тепер спробуйте підставити x=5
Отримали тотожність і перевірили єдиний правильний розв'язок ірраціонального рівняння x=5.
2. Метод заміни змінних.( Даний метод зручно застосовувати тоді, коли при піднесенні обох частин рівняння до одного й того самого степеня виникають громіздкі перетворення.) 
Розв’язок полягає в замінні кореневого виразу введенням нової змінної. Потім, розв’язавши утворене раціональне рівняння, маємо відкинути сторонні корені, повернутися до заміни й розв’язати відповідне ірраціональне рівняння.
Дома розвязавши рівняння,знайшов корені.
у= -1,5 не задовольняє умові 
.
Повернемось до заміни
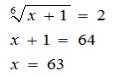
Відповідь : х = 63.
3. Метод розкладання на множники. ( Метод розкладання на множники полягає в розкладанні всіх доданків рівняння на множники, прирівнявши їх до нуля. Потім, знайшовши ОДЗ, маємо розв’язати сукупність множників як окремого рівняння.)
В нашому рівнянні 
є наявний однаковий множник 
, який треба винести за дужки і розкласти ліву частину на множники.
;
або 
Відповідь: х = - 6 ; х= 7.
4. Графічний метод. (Графічний метод базується на побудові графіків відповідних функцій, які стоять в обох частинах рівняння, та знаходженні їхніх точок перетину, що є відповідно розв’язками даного рівняння. Недоліком даного методу, є те , що для більшості функцій ми не зможемо знайти точного розв’язку.) 
.
Рівняння 
розв’язується графічно. Побудувавши графіки функцій 
(вітка параболи) та 
(гіпербола) в одній системі координат, ми отримаємо точку перетину А( 3;1), абсциса якої і є розв’язком рівняння: х=3
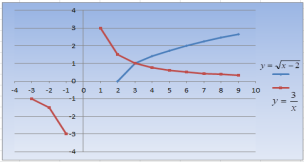
Учитель. Як ви вважаєте , який висновок можна зробити, виконуючи це завдання? При розв’язуванні будь-якого ірраціонального рівняння треба спочатку уважно роздивитися й проаналізувати умову рівняння, а потім визначитися з методом розв’язування рівняння. Цей метод називається – метод « пильного погляду».
(Після презентацій учні класу отримують буклети із алгоритмами розв’язування ірраціональних рівнянь за допомогою розглянутих методів).
IV. Застосування здобутих знань у видозмінених умовах шляхом виконання пробних вправ.
Учитель. Щоб закріпити щойно почуте й побачене, пропоную вам, використовуючи метод, який ви не досліджували вдома, розв’язати ірраціональні рівняння. У кожній групі є консультант, до якого ви можете звернутися за потреби й отримати допомогу, якщо зайшли в глухий кут. (Учні отримають метод вчителем, який вони не готували вдома, працюють у групах.) Увага на екран.
1. Виберіть ірраціональнє рівняння до вашого метода:
- піднесення до степеня – група 4;
- заміна змінної – група 2 ;
- розкладання на множники – група 1 ;
4. графічний – група 3 .
|
Рівняння |
Методи розв’язування |
|||
|
|
1 |
2 |
3 |
4 |
|
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
|
|
|
|
4) |
|
|
|
|
|
Рівняння |
Методи розв’язування |
|||
|
|
1 |
2 |
3 |
4 |
|
1) |
+ |
|
|
|
|
2) |
|
+ |
|
|
|
3) |
|
|
|
+ |
|
4) |
|
|
+ |
|
Після розв’язання рівнянь учні виконують самоперевірку, один з групи коментує біля дошки вибраний метод для даного ірраціонального рівняння.( фото розв’язування завдання один учень з групи відправляє на сайт – Classroom для обговорення).
1 група. Метод розкладання на множники.
У 4 рівнянні 
наявний однаковий множник 
, який треба винести за дужки й розкласти ліву частину на множники.
Розв'язання. ; 
або 
Відповідь : х= 5
Ми вважаємо, що цей метод був виправданим для виконання поставленої мети.
2 група. Метод заміни змінних.
Показники коренів другого рівняння 
2 і 4, 4 у 2 рази більше, ніж 2. Тому треба ввести нову змінну й прийти до квадратного рівняння.
Розв'язання. ; 
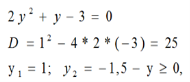
Повертаемося до заміни :
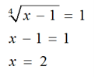Відповідь : х = 2.
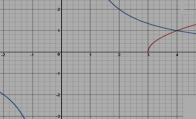3 група. Графічний метод. Ми вважаємо,що для 3 рівняння треба використати графічний метод. 
Побудувавши графіки функцій в програмі GeoGebra :
(вітка параболи) і 
(гіпербола) в одній системі координат, ми отримаємо точку перетину А(4;1), абсциса якої і є розв’язком рівняння: Відповідь: х=4.
На нашу думку, такий метод скорочує час на виконання завдання і є цілком виправданим? Так,але недоліком даного методу, є те, що для більшості функцій ми не зможемо знайти точного розв’язку.
4 група. Метод піднесення обох частин рівняння до одного степеня .
У першому рівнянні 
ми бачємо в лівій і правій частинах корінь другого степеня, тому використовуємо метод піднесення до степеня.
;
Висновок: знання правил, формул і методів розв’язання рівнянь може суттєво скоротити час на виконання завдання.
V.Релаксація.
Учитель. Дякую всім за практичну роботу. Думаю, нам час відпочити. Увага на екран. Сконцентруйтеся на математичних записах. Учні відповідають на питання.
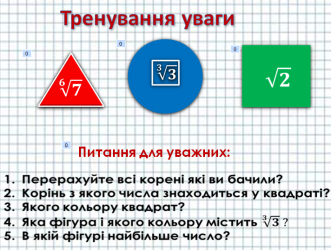
VI.Застосування ірраціональних рівнянь у житті сучасної людини:
Існує думка, що математика, яка вивчається в школи, не має практичного застосування в житті. Але мені не хочеться з цим погоджуватися. Виявляється, ірраціональні рівняння застосовуються не тільки в математиці.
-
2. 
3. 
4.
VII Готуємося до ЗНО.
Учитель. Добре,а зараз розв’яжімо рівняння із матеріалів ЗНО, під час виконання яких могли знадобитися здобуті нами сьогодні знання( учень розв’язує біля дошки)
1.ЗНО 2006 №26
ОДЗ :
;
х= -3 ; х= 2 – сторонній корінь.
Перевіряемо ОДЗ : х= -3; 9- (-3) – 6 = 6 
.
Відповідь: х= - 3.
2. ЗНО 2008 №28. (Учні самостійно розв’язують це рівняння , потім учням треба знайти правильну відповідь на бланках з QR- кодом. Якщо вибір буде правильним, тоді вони почують музику,яка грала на початку уроку)
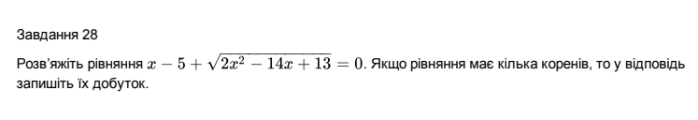
ОДЗ:
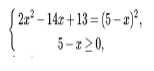
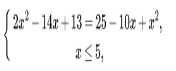
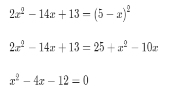
х= 6 – сторонній корінь.
Перевірка:
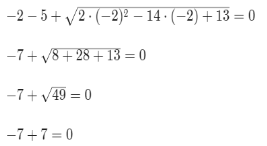
Відповідь: х= - 2.
QR- КОД :
Відповідь: х= - 2. Відповідь: х= 6.
V. Підведення підсумків уроку, оголошення домашнього завдання.
Учитель. На сьогоднішньому уроці ми ознайомилися з алгоритмом розв’язку ірраціональних рівнянь різними методами. Які ваші враження? Скористаймося прийомом незакінчених речень:
- У процесі роботи я зрозумів, що ….
- Обираючи певний метод, треба звертати увагу на….
- Я зрозумів усе, але хотів би, ще попрактикуватися з методом….
- ЗНО – не така вже й страшна річ, якщо…
(Учні завершують речення кількома словами).
Учитель. Молодці!
Засвоєння вами цих понять я перевірю за розв’язанням тестів в домашній роботі.
Якщо ви зрозуміли всі методи розв’язування рівнянь, то виконуете завдання з сайту «На урок» Хто не розібрався до кінця, то спочатку розв’яжіть тренувальні вправи на сайті «learningapps», а вже потім перейдіть на сайт «На урок».
Всім дякую за урок.
1
про публікацію авторської розробки
Додати розробку