6 клас. Математика Тема. Пропорції. Основна властивість пропорції.
Тема: Пропорції. Основна властивість пропорції.
Мета:
сформувати поняття пропорції; домогтися засвоєння основної властивості пропорції; сформувати вміння застосовувати поняття і основну властивість до розв'язування рівнянь;
Розвивати вміння працювати на результат, аргументувати власну думку, вести діалог – розвиток життєвих компетентностей;
Виховувати упевненість у власних силах.
Тип уроку: формування нових знань.


Чільне місце в системі моєї діяльності належить урокам. Саме на уроках учні отримують важливі теоретичні знання з математики, вчаться їх застосовувати на практиці. Конструюючи кожен урок, я враховую різні чинники, які впливають на розвиток уроку, як форму організації навчального процесу. Продумуючи урок, планую ситуацію, яка формує інтерес до вивчення конкретного матеріалу на етапі постановки мети, мотивації пізнавальної діяльності; спонукає до самостійності в процесі оволодіння змістом навчання на етапі осмислення і засвоєння; веде до використання їх у нових ситуаціях. Найчастіше використовую методи: проблемний виклад, пошуковий, дослідницький, евристичний тощо. Засобами реалізації проблеми вибираю роботу з текстом підручника, пошук фактів, асоціативний ряд, вивчення таблиць, графіків, перегляд презентацій, спілкування, короткі перевірочні роботи, математичні диктанти тощо.
Для створення проблемних ситуацій на уроках математики використовую: історичні екскурси, життєві факти, цікаві задачі. Роботу на уроці організовую так, щоб кожен учень працював активно, на повну силу, а наслідок – розвиток пізнавального інтересу, логічного мислення, формування чітких умінь і навичок.
Урок №3
Тема: Пропорції. Основна властивість пропорції.
Мета:
- сформувати поняття пропорції; домогтися засвоєння основної властивості пропорції; сформувати вміння застосовувати поняття і основну властивість до розв’язування рівнянь;
- Розвивати вміння працювати на результат, аргументувати власну думку, вести діалог – розвиток життєвих компетентностей;
- Виховувати упевненість у власних силах.
Тип уроку: формування нових знань.
Методи: словесні: розповідь, евристична бесіда, коментар, використання
ключових слів,
практичні: розв’язування вправ, метод повторення, самоперевірка за
зразком.
Обладнання: роздавальні матеріали, опорний конспект, картки;
Структура уроку:
- Організаційний момент
- Перевірка домашнього завдання
IIІ. Відтворення і коригування опорних знань
IV. Мотивація навчання
V. Сприйняття та усвідомлення нового матеріалу
VІ. Осмислення нового матеріалу
VІІ. Відпрацювання навичок застосовувати нові знання
VIІІ. Підсумок уроку
ІХ. Домашнє завдання.
Хід уроку.
I. Організаційний момент
Гра „Пароль” Вчитель привітавшись, не пропонує сісти, а просить назвати, не повторюючись (ланцюжком), ключове для матеріалу попереднього уроку слово.
Доброго дня, діти! Сьогодні урок розпочнемо з гри. Зараз кожен з вас назве своєрідний допуск до уроку, пароль - математичний термін з матеріалу попереднього уроку.
(Діти називають: частка, відношення, члени відношення, попередній член, наступний член, основна властивість відношення, карта, масштаб, натуральні числа, дробові числа, знак ділення «:», риска дробу, синонім).
II. Перевірка домашнього завдання.
Діти! Народна мудрість говорить «Тільки після невтомної праці з’явиться талант». Тому всіх прошу до роботи! Мисли активно, дій оперативно – ці слова нехай будуть девізом нашої спільної роботи сьогодні.
- Взаємоперевірка (обмінюються зошитами).
- Обговорення розв’язку задачі Мудрої Сови. (визначити кращий і оцінити)
ІІІ. Відтворення і коригування опорних знань.
Емоційна хвилинка :
Махараджа вибирав собі міністра. Він оголосив, що візьме того, хто пройде по стіні навколо міста з глечиком, доверху наповненим молоком, і не проллє навіть краплі. Багато було охочих, але по дорозі їх відволікали і вони розливали молоко. Але ось пішов один чоловік. Навколо нього кричали, стріляли, його по-всякому лякали і відволікали, але він не розлив молока.
- Ти чув крики, постріли? — запитав його потім Махараджа.
- Ти бачив, як тебе лякають?
- Ні, я дивився тільки на молоко — відповів той.
Не бачити і не чути нічого стороннього — от як повинна бути зосереджена
увага! Тепер ми перевіримо вашу увагу.
Записати дату і виконати завдання з дошки. Перевірка здійснюється учнями у парах за відкидною дошкою.
Завдання 1.Знайдіть відношення:
- 45 до 5;
- 4до 24;
-
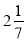 до
до 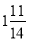 ;
;
- 4,8 до 0,12;
- 1,8 м до 30 см;
- 1 кг до 125 г.
Розв’язання.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5)![]() ;
;
6) ![]() .
.
(Учні, які мають високий і достатній рівень отримують додатково картки.)
Задача 2.У сплаві, маса якого 250 кг, міститься 20 кг міді. У скільки разів маса сплаву більша за масу міді, яку він містить? Яку частину сплаву становить мідь?
Розв’язання.
- 250:20=12,5 разів маса сплаву більша за масу міді, яку він містить.
- 20:250=0,08 частину сплаву становить мідь.
Завдання 3. Збільшиться чи зменшиться і в скільки разів відношення, якщо:
1)попередній член зменшити в 5 разів;
2)наступний член зменшити в 6 разів;
3)попередній член збільшити в 9 разів, а наступний зменшити у 2 рази;
4)наступний і попередній члени збільшити відповідно в 4 і 12 разів?
Розв’язання.
1)Якщо попередній член зменшити в 5 разів, то відношення зменшиться в 5 разів;
2)Якщо наступний член зменшити в 6 разів, то відношення збільшиться в 6 разів
3)Якщо попередній член збільшити в 9 разів, а наступний зменшити у 2 рази, то відношення збільшиться в 18 разів;
4)Якщо наступний і попередній члени збільшити відповідно в 4 і 12 разів, то відношення збільшиться в 3 рази.
(Правильно розв’язані задачі і вправи учні позначають у картках самооцінювання.)
- Фронтальне опитування: методичний прийом „Вірю – не вірю”.
1) Чи вірите ви, що частку двох чисел називають відношенням? (Так)
2) Чи вірите ви, що відношення чисел a і b показує, у скільки разів число a більше за число b або яку частину число a становить від числа b? (Так)
3) Чи вірите ви, що у відношенні а:b а називають наступним членом? (Ні)
4) Чи вірите ви, що у відношенні a:b b називають попереднім членом? (Ні)
4) Чи вірите ви, що відношення не зміниться, якщо його члени помножити або поділити на одне й те саме число, яке не дорівнює нулю? (Так)
5) Чи вірите ви, що відношення дробів не можна замінити відношенням натуральних чисел? (Ні)
6) Чи вірите ви, що швидкість – відношення довжини пройденого шляху до часу, за який пройдено цей шлях? (Так)
7) Чи вірите ви, що масштаб карти –це відношення відстані на карті до відповідної відстані на реальній місцевості? (Так)
8) Чи вірите ви, що ціна - це відношення кількості одиниць товару до відношення вартості товару? (Ні)
9) Чи вірите ви, що продуктивність праці – це відношення обсягу виконаної роботи до часу, за який було виконано цю роботу? (Так)
10) Чи вірите ви, що густина – це відношення маси речовини до її об’єму? (Так)
IV. Мотивація навчання
1) Методичний прийом „Відповідь із рецензією” (один учень відповідає, інший рецензує). Не можна одразу надавати слово тим учням, що перші справилися із завданням. Потрібно надати можливість слабшим учня проявити себе, а сильніші скажуть чи згодні вони, чи може є доповнення. Це дасть змогу товаришеві по класу дати підтримку і всі учні бачитимуть значимість своєї роботи.
- Яке відношення чисел 3,6 і 0,4? (9)
- Яке відношення чисел 1,8 і 0,2? (9)
- Чи можна вважати рівними дані відношення, тобто 3,6:0,4=1,8:0,2?
- Наведіть приклади рівних відношень.
а) 15:20=6:8;
б) 18:6=3:1;
в) 42:7=24:4;
г) 40:80=2:4.
Зробіть висновок.
V. Сприйняття та усвідомлення нового матеріалу
- Методичний прийом «Сторінка довідника». Створення опорного конспекту.
Наголосити учням, що він допоможе при підготовці до уроку вдома і при відповіді на наступному уроці. Опорний конспект треба запам’ятати!
Вчитель: Хто може перекласти на латину слово «співрозмірність»? (Імовірно, що жоден учень не знає відповіді на питання.) Але ви, напевне, чули слово «пропорція», яке і означає латинською співрозмірність.
Пропорція - математичний термін. Сьогодні на уроці ми дізнаємось,що він означає і дізнаємось про її цікаві властивості.
Рівність двох відношень називається пропорцією. У буквеному вигляді пропорцію можна записати так: ![]() або
або ![]() .
.
Наведені записи читають: «відношення а до b дорівнює відношенню c до d» або «а відноситься до b, як c відноситься до d».
Числа a і d називають крайніми членами пропорції, а числа b і c називають середніми членами пропорції.
Середні члени пропорції крайні члени пропорції
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() або
або ![]()
![]() крайні члени пропорції Середні члени пропорції
крайні члени пропорції Середні члени пропорції
2) Методичний прийом „Еврика”.
Вчитель. Які у пропорції 15:20=6:8 крайні члени?
Учні. У пропорції 15:20=6:8 числа 15 і 8 крайні члени.
Вчитель. Які у пропорції 15:20=6:8 середні члени?
Учні. У пропорції 15:20=6:8 числа 20 і 6 крайні члени.
Вчитель. Знайдіть добуток крайніх членів пропорції.
Учні. Добуток крайніх членів пропорції дорівнює 120.
Вчитель. Знайдіть добуток середніх членів пропорції.
Учні. Добуток середніх членів пропорції дорівнює 120.
Вчитель. Яку закономірність можна помітити?
Учні. Добуток крайніх членів пропорції дорівнює добутку середніх членів пропорції.
Вчитель. Ця властивість притаманна будь-якій пропорції. Вона виражає основну властивість пропорції:
Добуток крайніх членів пропорції дорівнює добутку середніх членів пропорції.
Як можна записати основну властивість пропорції у буквеному вигляді?
Учні. Це означає, якщо ![]() , то ad=bc.
, то ad=bc.
Як наведена властивість дає можливість встановити рівність двох відношень?
Учні. Наведена властивість дає можливість установлювати рівність двох відношень, не знаходячи їх значень.
Вчитель. Наведіть приклади.
Учні. Наприклад, щоб встановити, чи утворюють відношення ![]() і
і![]() пропорцію, досить перевірити, чи рівні добутки
пропорцію, досить перевірити, чи рівні добутки![]() і
і ![]() .
.
Отримуємо: ![]() =10,
=10, ![]() =10. Отже, маємо пропорцію
=10. Отже, маємо пропорцію ![]() =
=![]() .
.
Вчитель. Зазначте, які пропорції випливають з рівності ad=bc?
Учні. З рівності ad=bc випливають, наприклад, і такі пропорції: ![]() ,
,![]() .
.
Історична довідка «творчої групи».
Слово пропорція походить від латинського proportio (співвідношення, розмірність). Теорію пропорцій створили давньогрецькі вчені, зокрема Теет (410 – 368 до н. е.) і Евдокс (408 – 355 до н. е.). З пропорціями учні школи Піфагора пов’язували думки про співзвучні акорди в музиці і гармонію у Всесвіті, про порядок у природі. Пропорції використовували з давніх-давен. У стародавні часи пропорції відігравали тим значнішу роль, що задачі розв’язувалися без рівнянь, а якраз за допомогою пропорцій. Крім того, в Стародавній Греції дроби вважалися не числами, а відношеннями чисел. Тому дії над дробами теж приводили до використання пропорцій. Цим пояснюється значна увага, яку приділяли вивченню пропорцій як у стародавні часи, так і в середні віки.
Фізкультхвилинка.
Раз-два! Потягнулись,
І прогнулись, розігнулись.
Ваші м’язи всі проснуться,
Ваші губи усміхнуться.
А тепер - до роботи.
VІ. Осмислення нового матеріалу
1) Методичний прийом „Хто більше?”
Два учні (хто якнайшвидше і найбільше записують пропорції, дописавши відношення до рівності 6:9).
1 учень 2:3=6:9, 12:18=6:9, ![]() =6:9 і т. д.
=6:9 і т. д.
2 учень 24:36=6:9, 2:3=6:9, ![]() =6:9 і т д.
=6:9 і т д.
Вчитель. Скільки можна записати пропорцій?
Учні. Безліч.
2)Методичний прийом „Коментоване письмо” (Учні пишуть під диктовку вчителя потім читають уголос. Сприяє виробленню навичок записувати речення формулою і навпаки).
Запишіть у вигляді пропорції висловлення:
- 2 відноситься до 7, як 6 відноситься до 21;
- Відношення 7,2 до 0,8 дорівнює відношенню 0,09 до 0,01;
-
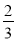 відноситься до
відноситься до 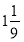 , як
, як 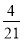 відноситься до
відноситься до 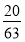 .
.
3) Методичний прийом „Невтручання”.
Складіть усі можливі пропорції, які випливають з рівності ![]() .
.
Розв’язання.
4:18=2:9, 18:9=4:2, 9:18=2:4, 9:2=18:4,
18:4=9:2, 2:4=9:18; 4:2=18:9; 2:9=4:18.
Висновок. Пропорція буде істинна, якщо поміняти місцями крайні члени, поміняти місцями середні члени, одночасно поміняти крайні та середні члени та ліву й праву частини пропорції.
VІІ. Відпрацювання навичок застосовувати нові знання
Методичний прийом „Працюємо за зразком”. Разом з учнями складаємо алгоритм розв’язування рівнянь виду ![]() , де невідомий один із членів.
, де невідомий один із членів.
- Записати основну властивість пропорції – ad=bc.
- Знайти невідомий множник.
(Учні виконують завдання і перевіряють у парах)
Впр. 605 Розв’яжіть рівняння:
1) ![]() ; 2)
; 2) ![]() ;
;
![]() ;
; ![]() ;
;
![]()
![]() ;
; ![]()
![]() ;
;
![]() 5.
5. ![]()
![]() .
.
3)
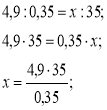
х=490.
4) ![]()
![]()
![]()
![]() 13,5.
13,5.
5) ![]()
![]()
![]() ;
;
![]()
![]() 6.
6.
6) ![]()
![]() ;
;
![]()
![]()
VIІІ. Підсумок уроку
З якою темою познайомилися? Чого навчились?
Запишіть нові терміни, про які ішла мова на уроці.
Підрахунок балів у картках самооцінювання та оголошення оцінок.
ІХ. Домашнє завдання.
п.20 опрацювати
Виконати № 600, № 602, № 606
Скласти повідомлення « Пропорція це..» і розповісти батькам.
Картка самооцінювання
|
1 |
Домашнє завдання |
|
|
2 |
Задачі Мудрої Сови. |
|
|
3 |
Індивідуальні задачі |
|
|
4 |
Завдання 1.Знайдіть відношення: |
|
|
5 |
„Вірю – не вірю”. |
|
|
6 |
Відповідь із рецензією |
|
|
7 |
Виконання вправ |
|
|
|
|
|
![]()


про публікацію авторської розробки
Додати розробку
