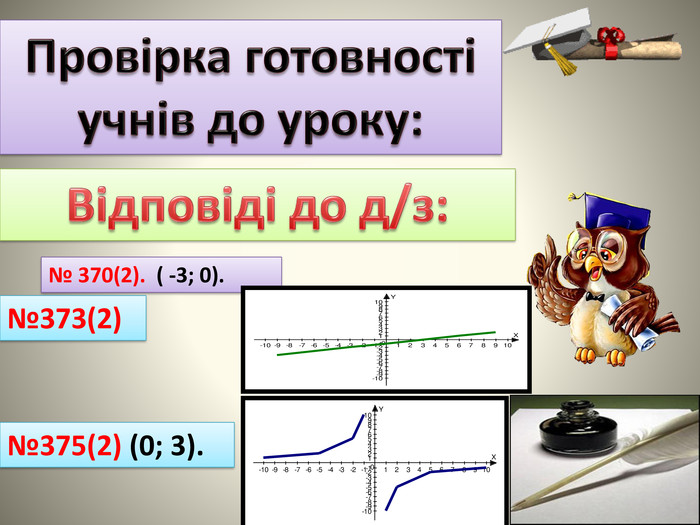
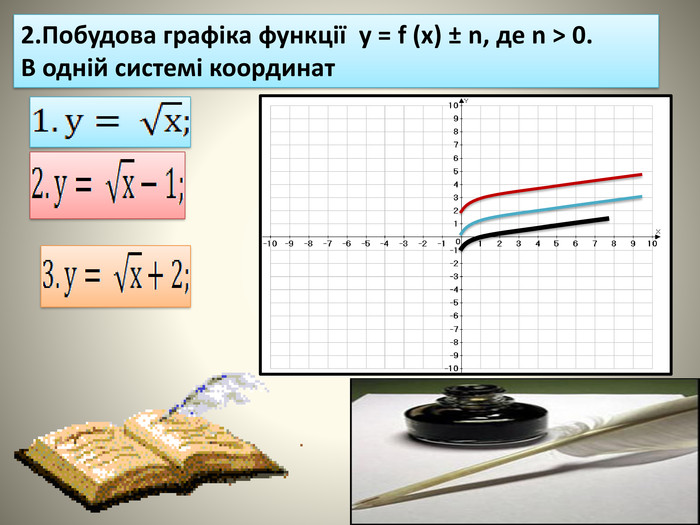
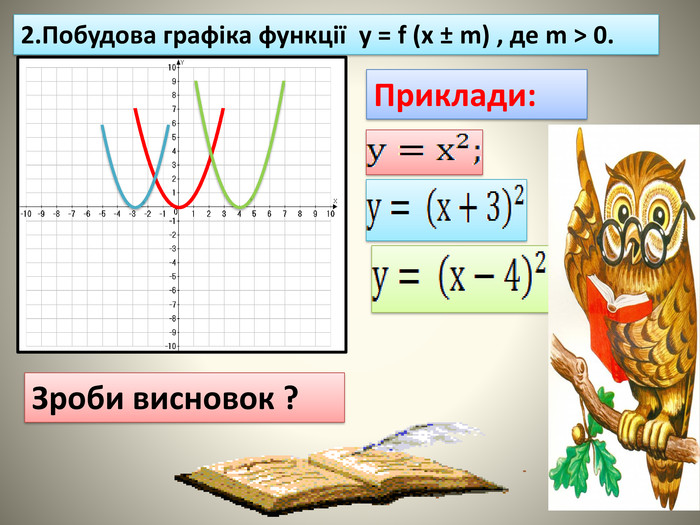
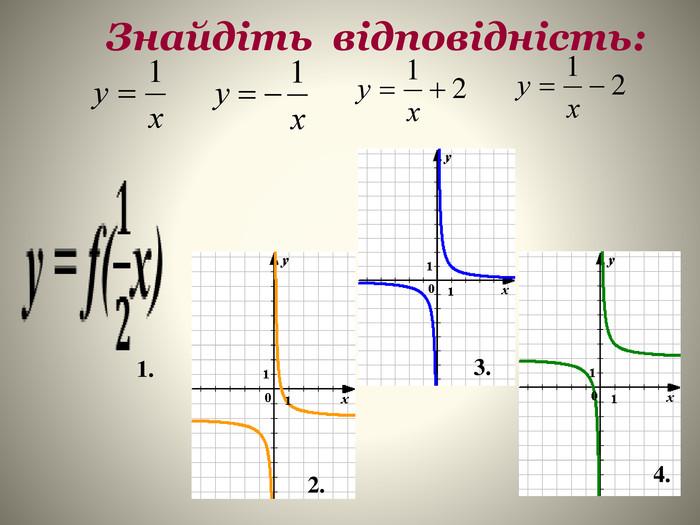
9-кл.Алгебра.Презентація:,, Найпростіші перетворення графіків функції.''
Про матеріал
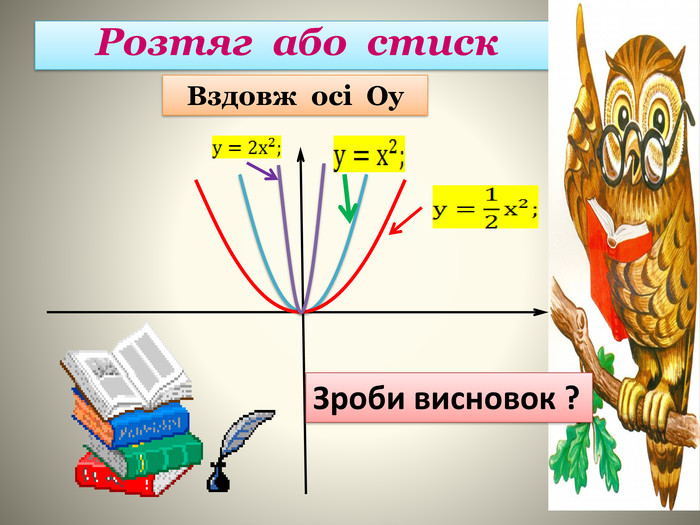
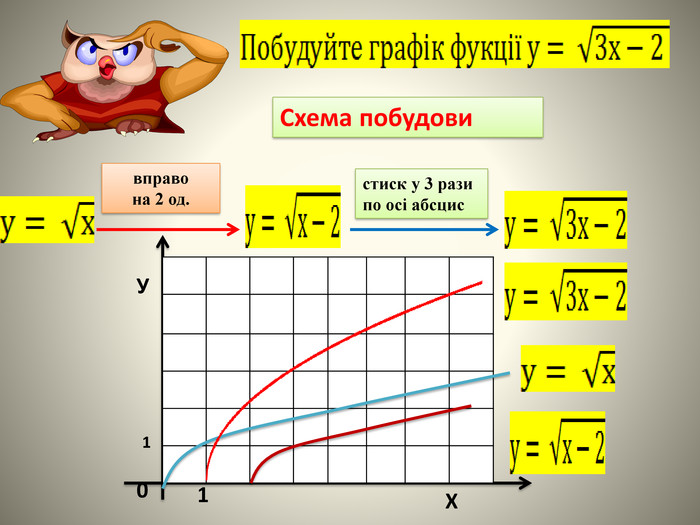
В даній презентації на основі основних видів перетворень фукції показані приклади практичного спрямування для усвідомленя властивостей перетворень та умінь їх застосовувати для розв'язування прикладних задач.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку