Активізація пізнавальної діяльності учнів на уроках математики

Навчання - це праця, що потребує великої напруги сил. І все ж стійкий інтерес учнів до предмету іде через цікавість і допитливість і це значною мірою визначає успіх учнів у навчанні.

Знання, отримані в готовому вигляді, як правило, викликають труднощі учнів у їх застосуванні до пояснення спостережуваних явищ і вирішення конкретних завдань. Одним із суттєвих недоліків знань учнів залишається формалізм, який проявляється у відриві завчених учнями теоретичних положень від уміння застосувати їх на практиці. 

Ставлення учнів до навчання  зазвичай характеризується активністю.  З активністю безпосередньо сполучається ще одна важлива сторона мотивації навчання учнів це самостій-ність,здатність самим вчитися без допомоги дорослих і вчителів. Пізнавальна активність і са-мостійність невід'ємні один від одного: більш активні школярі, як правило, і більш самостійні; недостатня власна активність учня ставить його в залежність від інших і позбавляє самостійності. 
У педагогічній  практиці використовуються різні шляхи активізації пізнавальної діяльності, основні серед них - різноманітність форм, методів, засобів навчання, вибір таких їх поєднань, які у ситуаціях, що виникають, стимулюють активність і самостійність учнів. 
Можна стверджувати, що нові технології самостійного навчання мають на увазі, перш за все підвищення активності учнів: істина, здобута шляхом власного напруги зусиль, має величезну пізнавальну цінність. 
Звідси можна зробити висновок, що успіх навчання в кінцевому підсумку визначається ставленням учнів до навчання, їх прагнення до пізнання, усвідомленим і самостійним придбання знань, умінь і навичок, їх активністю. 

Існують основні способи активізації пізнавальної діяльності: 
1. Спиратися на інтереси учнів і одночасно формувати мотиви навчання, серед яких на першому місці виступають пізнавальні інтереси, професійні схильності; 
2. Включати учнів у вирішення проблемних ситуацій; 
3. Використовувати дидактичні ігри та дискусії; 
4. Використовувати такі методи навчання, як бесіда, приклад, наочний показ; 
5. Стимулювати колективні форми роботи, взаємодію учнів у навчанні. 
Дані способи активізації пізнавальної діяльності здійснюються за допомогою різних методів навчання.

 

Класифікація методів активізації навчально-пізнавальної діяльності

 

Імітаційні методи		Неімітаційні методи
Ігрові	Неігрові	Бесіда	«Асоціатив-ний кущ»
Метод інсценуван-ня	Метод аналізу конкретної ситуації	Прес-конференція	«Мікро-фон»
Ділові ігри	«Мозкова атака»	Дискусія	«Мозаїка»
	Метод круглого столу	Урок із заздалегідь запланованими помилками	Робота в парах
	Моделювання виробничої ситуації	Інтелектуальна розминка	Робота в групах

 

До ігрових належать розігрування ролей і ділові ігри різних модифікацій. Вони суттєво допомагають закріпленню й поглибленню знань, отриманих під час бесід, лекцій, розповідей, семінарів, практичних занять, удосконаленню практичних навичок та вмінь, їх застосуванню, творчому використанню у вирішенні професійних проблем, створенню умов для активного обміну досвідом. Так при вивченні теми «Розв`язування трикутників» можна провести ділову гру «Геодезист»

 

Тема. Розв´язування трикутників.

Мета: засвоїти методи розв´язання задач на розв´язування трикутників, навчитись застосовувати здобуті знання підчас розв´язування практичних задач; активізувати пізнавальну активність учнів; розвивати вміння міркувати, аналізувати і робити висновки; ознайомити учнів з професією геодезиста.

Тип уроку. Ділова гра

 

Хід уроку.

 

І. Мотивація навчальної діяльності.

Є професії, які вимагають дуже часто розв´язувати трикутники. Насамперед цим займаються геодезисти. Яке б велике будівництво не розпочиналось, яка б дорога не будувалась, першими туди йдуть геодезисти, щоб зняти план місцевості та охарактеризувати рельєф. Коли з на основі їх матеріалів у проектних організаціях опрацюють проект, геодезисти знову міряють кути, розв´язують трикутники, забивають кілочки – «прив´язують» опрацьований матеріал до місцевості. А навіщо вони розв´язують трикутники? Щоб визначити потрібні відстані, не вимірюючи їх безпосередньо. Є ще спеціалісти, які розв´язують подібні задачі в шахтах, тунелях,  метро та інших підземних розробках. Це маркшейдери. Їм також часто доводиться розв´язувати трикутники.

 

ІІ. Повідомлення мети і задач уроку.

На уроці кожен з вас уявить себе геодезистом і розв´яже реальну практичну задачу, яка потребує знань з геометрії.

 

ІІІ. Організація роботи. Правила гри

Клас ділиться на групи. Мета кожної групи – якомога швидше і правильно розв´язати практичні задачі, запропоновані вчителем. На обговорення задач дається 10 хвилин. Задачі записуються в зошит. Кожен учень групи повинен пояснити свою задачу. Переможцем буде та група, яка першою правильно виконає розрахунок.

 

ІV. Підготовчий етап

Питання до груп.

1. За допомогою яких приладів вимірюються невеликі відстані, кути?
2. Які основні теореми застосовуємо під час розв´язування трикутників?

 

 

V. Ознайомлення та розв´язування практичних задач

Учні знайомляться з умовами задач, потім розв´язують їх.

Задача 1

Знайти відстань між двома доступними пунктами, якщо між ними безпосередньо вимірювання відстані неможливе.

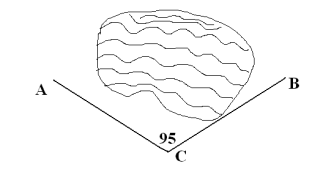
Для вимірювання відстані між опорами А і В високовольтних ліній, які розділені водою, вибрали пункт С і виміряли СА = 40 м, СВ= 30 м, 95⁰. Визначити АВ.

 

Задача 2

Визначити ширину річки, якщо башта, висота якої 65 м, знаходиться на березі річки і її видно з другого берега  під кутом 65^о.

 

 

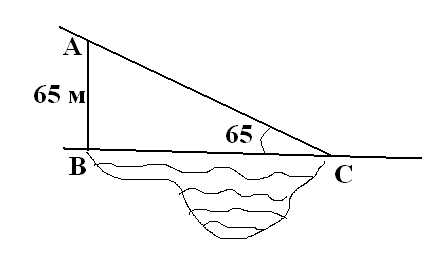
Задача 3.

Знайти відстань між двома недоступними предметами В і С, що знаходяться на протилежних берегах річки, якщо АС = 8 м, ∠С=35^о, ∠А = 70^о.

 

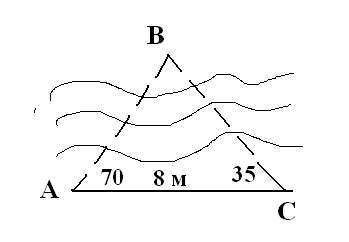
Задача 4.

Знайти відстань від острова В, розташованого на озері до пункту А, який знаходиться на березі, якщо відстань АС =18 м, і кути α = 100^о, β=50^о. (Острів прийняти за точку)

 

 

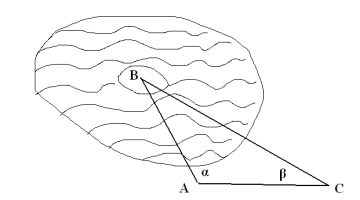
Задача 5.

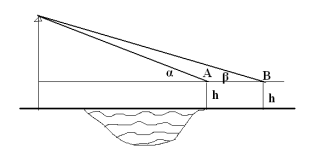
З двох точок А і В, відстань між якими 50 м, вершину вишки видно під кутами α=50^о і β = 30^о. Знайти висоту вишки, якщо зріст людини h = 1,64м

 

VІ. Звіт груп.

Для відповіді біля дошки викликається по 1 учень. Учні іншої групи ставлять питання і виправляють помилки.

 

VІІ. Домашнє завдання

 

VІІІ. Підбиття підсумків уроку

Самооцінка.

Чи кожен учень групи зміг висунути свою пропозицію?

Чи все обговорили?

Чи виконали задачу до кінця?

Підсумок роботи вчителем.

Яка група швидко й правильно виконала завдання?

Як працював клас? Як працювали окремі учні?

Виставлення оцінок.

 

На уроках математики в 5 класі при вивченні тем «Додавання і віднімання натуральних чисел» використовую гру «Магічні квадрати», «Математичні сходинки». В 6 класі на закріплення та перевірку умінь з теми «Прямокутна система координат на площині. Координати точок.» проводжу конкурс художників, як самостійну творчу роботу для учнів. Різноманітні малюнки ,побудовані за допомогою точок із координатами, покажуть не тільки засвоєння теми, а й розумові здібності та творчу уяву учнів .Можна запропонувати й обернену вправу: намалювати самим малюнок за допомогою замкненої ламаної , і записати координати вершин. На геометрії це можуть бути «Конкурс геометрів», «Аукціони знань» та інші. Гру можна розглядати як працю і як творчість .Під час гри діти вчаться бути сконцентрованими, мислити самостійно, розвивається увага, тяга до знань.

Неімітаційні методи активізації навчально-пізнавальної діяльності

Нарівні з імітаційними активними методами навчання в дидактичному процесі повинні широко застосовуватися й неімітаційні, бо, по-перше, не завжди через певні об'єктивні та суб'єктивні причини вдається організувати заняття в ігровій формі, по-друге, традиційні методи навчання потребують пожвавлення, внесення певних нестандартних методичних прийомів.

• Урок-бесіда – «діалог з аудиторією» – найбільш поширена й порівняно проста форма активного залучення учнів до навчального процесу. Вона передбачає безпосередній контакт учителя з аудиторією, що дає змогу зосередити увагу учнів на найбільш важливих проблемах теми, яка вивчається, визначити зміст і темп викладу навчального матеріалу з урахуванням рівня підготовленості та освіти аудиторії.

Участь учнів у бесіді забезпечую різними прийомами, такими як: запитання до аудиторії (спантеличення). Вони носять інформаційний характер, тобто спрямовані не на контроль, а на з'ясування думок і рівнів поінформованості учнів з проблеми, що вивчається, актуалізації знань, необхідних для її розуміння, та визначення ступеня готовності до сприйняття матеріалу лекції. Коли рівень підготовленості слухачів досить високий, можна ставити проблемні запитання, які, вказуючи на сутність навчальної проблеми, спонукають до обмірковування проблемної ситуації. Учні, замислюючись над змістом ситуації, виявляють інтерес до теми уроку, позитивно ставляться до проблем, які підлягають вивченню, намагаються самостійно або разом з педагогом розв'язати проблемну ситуацію. Таким чином, відбувається всебічний і глибокий аналіз проблеми. 

До уроку-прес-конференції залучаються заздалегідь ознайомлені з проблемою учні: тоді вони готують запитання, які групуються за проблемами, і для відповіді на них запрошуються кращі учні. Учні готують питання протягом заздалегідь,  після чого, протягом 3-5 хвилин, один з учнів,готує відповідь та пояснює її іншим . У ролі відповідача може бути також учитель, який по запитаннях пояснює матеріал, а потім  оцінює кращі запитання та узагальненює вивчений матеріал. Далі наведений урок – прес-конфененція, проведений у 9 класі при підведення підсумків вивчення теми «Відсоткові розрахунки»

 

Тема. Відсоткові розрахунки. Розв´язування задач

Мета: узагальнити і систематизувати знання, вміння і навички учнів розв´язувати задачі на відсотки; показати на прикладах практичну спрямованість математичних знань, забезпечити політехнічну підготовку і профорієнтацію учнів; сприяти формуванню економічної грамотності, моральних і ділових якостей учнів; розвивати пам´ять, логічне мислення, мовлення учнів; формувати бажання вчитися.

 

Тип уроку: урок – прес-конференція

 

Хід уроку.

 

На конференції присутні кореспонденти газет, підприємці, промисловці. За столом сидять спеціалісти банку, економісти, хіміки – технологи.

На дошці написано:

Все підлягає обчисленню й вимірюванню. Немає понять загальніших, ніж число і простір.

Д. Дідро

І. Вступне слово вчителя

Україна має безліч економічних проблем, розв´язувати які доведеться вам. Тому кожному громадянину потрібна насамперед фундаментальна загальна підготовка. Сьогодні на уроці ми продовжимо вивчення теми «Елементи прикладної математики» та побачимо як практично використовуються знання і вміння, пов´язані з нашою темою в економіці, банківській справі, хімії.

Давайте пригадаємо найпростіші задачі на відсотки.

1. Як знайти р% від числа а?
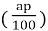
2. Як знайти число якщо р% від нього дорівнює а? (
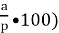
3. Як знайти відсоткове відношення чисел m і n? (

 

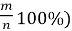
Складніші задачі на відсотки часто доводиться розв´язувати бухгалтерам та економістам, працівникам банків, технологам, які сьогодні присутні на на нашій прес-конференції та дадуть відповіді на запитання присутніх у залі кореспондентів газет, підприємців, менеджерів, спеціалістів у галузі маркетингу, промисловців.

Учні - кореспонденти газет, підприємці, менеджери, спеціалісти у галузі маркетингу, промисловці зарані знайшли і підготовили запитання.

 

ІІ. Прес- конференція

 

Запитання 1.

Підприємець, прізвище, ім´я

Банк приймає гривні під 21% річних а іноземну валюту під 9%річних. Як краще зберегти  на рік 200 000 гривень в гривневому депозиті чи в євро, якщо курс вважати незмінним?

 

Відповідь працівника банку.

В гривнях через рік ви матимете 200 000(1 + 0,21)=242 000 (грн.).

200 000 : 10 = 20 000 (євро);   20 000(1 + 0,09) = 21 800 (євро) ;  21 800*10=218 000(грн.). Якщо ви покладете в гривнях, то матимете на 24 000 грн більше.

 

Запитання 2.

Кореспондент газети «Україна і бізнес»

Говорять, що гетьман Полуботок у 1723 році поклав до англійського банку великий капітал з України. У скільки раз збільшився цей капітал до 2014 року?

 

Відповідь.

Відсоткові гроші нараховуються за формулою А_n = A_0, де n – кількість років, р – відсоток, А₀ – початковий капітал.

В нашому випадку n=290 років ²⁹⁰ = 87029,88, тобто майже в 87 030 раз.

 

Запитання 3.

Кореспондент газети «Податки»

Як оподатковується заробітна плата?

 

Відповідь.

Із заробітної плати утримується 15% прибуткового податку, 1% профспілкових внесків, 3,6% єдиного соціального внеску. Наприклад, заробітна плата 2500 грн.

Прибутковий податок – 375 грн.

Профспілкові внески – 0,01* 2500 =  25 грн.

Єдиний соціальний внесок – 0,036* 2500=90 грн.

2500 – (375 + 25 + 90) = 2 010(грн.)

 

Запитання 4.

Економіст цукрового заводу

З цукрових буряків виходить 12%  цукру. Врожайність буряків у середньому становить 320 ц з гектара. Яку площу потрібно відвести під буряки, щоб отримати 1 т цукру?

 

Відповідь.

1 т = 10 ц,  10: (0,12*320) =0,26 (га) або 26 ар

 

Запитання 5.

Бухгалтер молокозаводу

З молока виходить 25% вершків, а з вершків – 20% масла. Скільки потрібно молока, щоб одержати 10 кг масла?

 

Відповідь.

Вихід масла з молока становить 0,25*0,2=0,05=5%. Кількість молока дорівнює 10 : 0,05 = 200 (кг)

 

Запитання 6.

Кореспондент газети «Порадниця»

Запитання до хіміка-технолога. Скільки треба долити води до 500 г 9% оцту, щоб одержати 6% оцет?

 

Відповідь.

Концентрація оцту дорівнює 0,09*500=45. Нехай потрібно долити х г води, отримуємо рівняння

(500 + х)*0,06 = 500*0,09

х= 250.

Отже, треба долити 250 г води.

 

Запитання 7

Підприємець.

Скільки золота 375-ї проби треба сплавити з 30 г золота 750-ї проби, щоб одержати золото 500-ї проби?

 

Відповідь.

Нехай потрібно х г золота 375-ї проби. Складаємо і розв´язуємо рівняння

0,375х + 30*0,75 = 0,5(х + 30)
          х=60

Відповідь. 60 грам.

 

ІІІ. Підсумок уроку

Оцініть свої враження від уроку.

Не цікаво, нічого не зрозумів ____________________

Все зрозумів, але залишились питання __________________

Все зрозумів, дізнався щось нове __________________

 

ІV. Домашнє завдання

Повторити типи задач на відсотки.      

 

 

Інтелектуальна розминка. Цей прийом можна застосовувати з метою привести учнів в активний «стартовий» стан за допомогою актуалізації їхніх знань, обміну думками, опрацювання загальної позиції та формування мотивації до навчально-пізнавальної діяльності. Водночас педагог має можливість з'ясувати рівень підготовленості учнів до розв'язання певних теоретичних і практичних проблем та набуття знань. Інтелектуальна розминка проводиться у швидкому темпі у формі експрес-опитування: педагог звертається до учнів із запитаннями, на які вони повинні дати коротку, але конкретну і змістовну відповідь. На проведення цього дидактичного заходу відводиться 10-15 хвилин. Розминка може передувати практично будь-яким груповим заняттям.

Серед інтерактивних методів навчання використовую метод побудови «асоціативного куща».

На початку уроку  визначаю одним словом тему, над якою проводитиметься робота, а учні згадують, що виникає в пам'яті стосовно цього слова. Спочатку висловлюються найстійкіші асоціації, потім - другорядні. Це  фіксується  у вигляді своєрідного «куща», який поступово «розростається». Цей метод універсальний, адже може використовуватися під час вивчення будь-якої навчальної дисципліни і на всіх етапах уроку.

Технологія «Мікрофон» надає можливість кожному сказати щось швидко, по черзі, відповідаючи на запитання або висловлюючи власну думку чи позицію.

Робота в парах

Роботу в парах можна використовувати для досягнення будь-якої дидактичної мети: засвоєння, закріплення, перевірки знань тощо. За умов парної роботи всі учні в групі отримують можливість говорити, висловлюватись. Робота в парах дає учням час подумати, обмінятись ідеями з партнером і лише потім озвучувати свої думки перед класом. Вона сприяє розвитку навичок спілкування, вміння висловлюватись, критичного мислення, вміння переконувати й вести дискусію. Під час роботи в парах можна швидко виконати вправи, які за інших умов потребують значної витрати часу

Робота в групах

Робота в групах надає всім учасникам можливість діяти, практикувати навички співробітництва, міжособистісного спілкування (зокрема, відпрацювання прийомів активного слухання, прийняття спільного рішення, узгодження різних поглядів). Роботу в групах слід використовувати тоді, коли необхідно розв'язати проблему, з якою важко впоратись індивідуально та коли одним із очікуваних результатів є набуття навичок роботи в команді.

Всі ці методи допомогають  підтримати в учнів інтерес до навчального матеріалу, їх активність на протязі всього уроку. Адже велике розумове навантаження, об’єм  інформації , викладений у підручнику, відбивають бажання вчитися. Тому потрібно так будувати свій урок, щоб кожний учень працював активно і захоплено .

  Різносторонньо і чітко спланована робота вчителя на кожному уроці –запорука того. що учні не тільки засвоять запропонований матеріал, а й зуміють застосувати його для різного типу задач. Розвивати  та активізувати розумову діяльність учнів на уроках математики можна тільки враховуючи вікові особливості дітей, враховуючи їх ініціативу .Адже знання учнів повинні бути здобуті своїм розумовим мисленням ,а не завчені механічно. Закріплені в результаті виконання творчого завдання чи іншого виду діяльності , вони проростуть в майбутньому шедеврами математичної думки .Важливе значення має формування в учнів умінь різносторонньо розглянути предмет задачі ,виділити необхідні суттєві зв’язки, скласти математичну модель до задачі з практичним змістом ,відчувати і усвідомлювати роль математики в процесі вивчення інших наук.                                                                                                          Римський імператор Цицерон говорив: «Інтелект – це здатність людини керуватися розумом, відчуттям і волею».

Тому учитель математики ,розвиваючи та активізуючи на своїх цікавих уроках розумову діяльність учнів, виховує інтелектуально розвинену особистість.

 

Література.

1. В.Н.Осинський.Активізація пізнавальної діяльності учнів на уроках математики в 9-10класах. Київ.Рад.школа.1980.
2. В.П.ІржавцеваЛ.Я.Федченко.Систематизація і узагальнення знань учнів в процесі вивчення математики.Київ.Рад.школа.1988.
3. Е.Г.Готман.Задача одна – розв’язки різні.Київ.Рад.школа.1988.
4. О.В. Кужель . Контрприклади в математиці. Київ.Рад.школа.1988.
5. Л . С. Карнацевич . Учить мыслить. Київ.Рад.школа.1982.
6. Дидактичні  ігри на уроках математики.                                                                                                                                  Харків. Основа. 2006                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                
7. Г.М .Возняк. К.П.Маланюк. Прикладна спрямованість шкільного курсу математики. Київ.  Рад.школа.1984.
8. В.Г.Коваленко.І.Ф.Тесленко.Проблемний підхід до навчання математики.Київ.Рад.школа.1985.
9. Учитель року – 2004. Цикли уроків з математики. Харків. Основа, 2005.
10. Л.А.Губа. Нетрадиційні уроки математики. Харків. Основа. 2005