Алгебра. 10 клас. Зростання та спадання функції. Екстремальні точки
План-конспект уроку алгебри
для 10 класу на тему:
“Зростання та спадання функції.
Екстремальні точки”
вчителя математики
Новгород-Сіверської державної
гімназії імені К.Д. Ушинського
Заєць Наталії Григорівни
Тема: Зростання та спадання функції. Екстремальні точки.
Мета: 1) навчальна: розкрити зміст даної теми, навчити учнів застосовувати похідну при розв’язанні задач, закріпити й узагальнити набуті теоретичні знання учнів про похідну функції;
2) виховна: виховувати дисциплінованість на уроці, уважність, охайність при виконанні письмових робіт та роботі з дошкою;
3) розвиваюча: розвивати самостійність мислення учнів, розвивати логічне мислення, вміння концентрувати увагу, розвивати інтерес до предмету.
Тип уроку: комбінований.
|
№ |
Етапи уроку |
Час |
ОМВ |
|
1. |
Організаційна частина |
1 – 2 хв. |
|
|
2. |
Актуалізація опорних знань |
4 – 7 хв. |
гра |
|
3. |
Оголошення теми, мети уроку |
1 – 2 хв. |
пояснення |
|
4. |
Вивчення нового матеріалу |
10 –15 хв. |
бесіда |
|
5. |
Закріплення вивченого матеріалу |
15 –20 хв. |
практичні методи, пояснення |
|
6. |
Підведення підсумків |
4 – 5 хв. |
бесіда |
|
7. |
Домашнє завдання |
1 – 2 хв. |
|
Хід уроку
1. Організаційна частина.
Привітання з учнями, перевірка присутніх.
2.Актуалізація опорних знань.
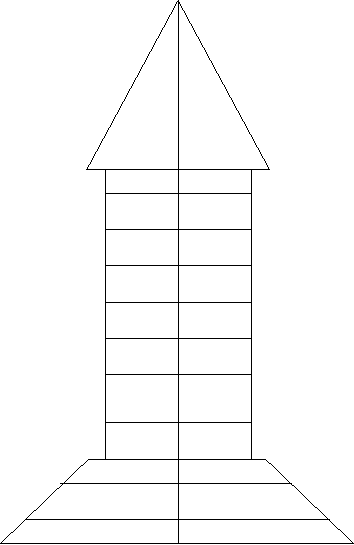 Згадаємо, як АН минулих уроках ми знаходили похідні. Для цього проведемо естафету “Хто швидше сяде в ракету”. На дошці зображено ракету, поділену навпіл. Весь класс ми ділимо на дві команди. Представники команд беруть навмання на столі картку із завданням, розв’язують його на дошці і першу відповідь записують на першій ступерні ракети, потім на другій і т. д. Переможе та команда, що першою заповнить відповідями всі ступені ракети.
Згадаємо, як АН минулих уроках ми знаходили похідні. Для цього проведемо естафету “Хто швидше сяде в ракету”. На дошці зображено ракету, поділену навпіл. Весь класс ми ділимо на дві команди. Представники команд беруть навмання на столі картку із завданням, розв’язують його на дошці і першу відповідь записують на першій ступерні ракети, потім на другій і т. д. Переможе та команда, що першою заповнить відповідями всі ступені ракети.
Завдання: знайти похідну:
1. y = cos 3x
2. y = e3x
3. y = ![]()
4. y = tg ![]()
5. y = cos 2 x
6. y = ![]()
7. y = sin ![]()
8. y = ![]()
9. y = ln 2x
10. y = 23x
11. y = x2 + 1
12. y = ex + ![]()
13. y = sin 2x
14. y = ![]()
15. y = ![]()
16. y = ctg 2x
17. y = 2 sin3 x
18. y = ![]()
19. y = cos 3x
20. y = ![]()
21. y = ln ![]()
22. y = ![]()
23. y = x3 - 4
24. y = e 2x + ![]()
3. Оголошення теми, мети уроку.
Досі ми знаходили похідні функцій. Сьогодні ж ми побачимо, де їх можна застосовувати. Отже, запишіть тему уроку: “Зростання та спадання функції. Екстремальні точки.” .
4. Вивчення нового матеріалу.
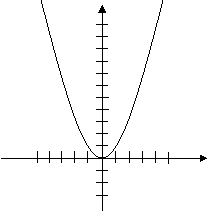
Розглянемо функцію у = x2 . Її графік має вигляд параболи (мал.1). Розглянемо функцію на (-∞;0). Знайдемо значення функції в точках x1 = -2, x2 = -1. Отже, y (-2) = 4, y(-1) = 1. y(-2) › y(-1).
Якщо значення функції в кожній наступній точці менші від значення функції в попередній точці, тоді функція називається спадною:
f (x+1) ‹ f (x).
Отже, функція у = x2 спадає на (-∞;0).
6
4
2
-4 -2 0 2 4 x
Мал. 1
Розглянемо тепер цю функцію на (0;+∞). Знайдемо значення функції в точках x3 = 1, x4 = 2. Отже, y (1) = 1, y(2) = 4. y(1) ‹ y(2).
Якщо значення функції в кожній наступній точці більші від значення функції в попередній точці, тоді функція зростає:
f (x+1) › f (x).
Отже, функція у = x2 зростає на (0;+∞).
Але не завжди просто знаходити значення функції, ми досі обирали точки довільним чином і знаходили в них значення функції. Не завжди модна легко побудувати графік функції і за ним визначити проміжки зростання і спадання функції. Для цього застосовують похідну. Розглянемо приклад.
Приклад 1.
Знайти проміжки монотонності фінкції:
![]()
Для того, щоб знайти проміжки монотонності, треба виконати наступні дії:
- Знаходимо похідну функції:
![]()
- Прирівнюємо похідну до 0:
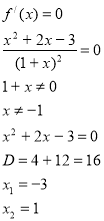
- Наносимо знайдені точки на числову вісь. На кожному з проміжків знайдемо значення похідної. Якщо f/ (x) › 0, тоді функція на даному проміжку зростає, якщо ж f/(x) ‹ 0 – спадає.

-3 -1 1
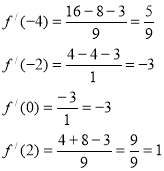
![]() › 0 – функція зростає
› 0 – функція зростає
f / (-2)‹ 0 - функція спадає
f / (0)‹ 0 - функція спадає
f / (2) › 0 - функція зростає
Отже, функція зростає на (-∞;-3)![]() (1;+∞) і спадає на (-3;-1)
(1;+∞) і спадає на (-3;-1)![]() (-1;1).
(-1;1).
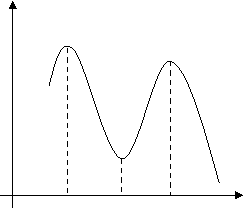
Розглянемо малюнок 2. Точки 1, 2, 3 даної функції є її екстремумами.
Відповідно x1, x3 – точки максимуму, x2 - точка мінімуму
 y
y
1 2
3
0 x1 x2 x3 x
Мал. 2
Екстремальні точки – це точки, в яких функція набуває відповідно найбільного чи найменшого значення порівняно із значеннями функції, яких вона набуває в точках, близьких до екстремальної. Такий екстремум називають локальним.
Не треба плутати локальний максимум (мінімум) з найбільшим (найменшим) значенням функції. Екстремумів функція може мати кілька, а найбільше і найменше значення – лише одне. Є два правила на знаходження екстремумів функції.
Перше правило:
- Знаходимо похідну функції.
-
Шукаємо критичні точки функції, прирівнючи похідну до 0:
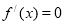 .
.
-
Перевіримо зміну знака похідної у кожній критичній точці. Якщо
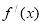 при переході через критичну точку (зліва направо) змінює знак з “+” на “ - ”, то ця точка є точкою максимуму, з “ - ” на “+” – точка мінімуму, не змінює знак – дана точка не є точкою екстремуму.
при переході через критичну точку (зліва направо) змінює знак з “+” на “ - ”, то ця точка є точкою максимуму, з “ - ” на “+” – точка мінімуму, не змінює знак – дана точка не є точкою екстремуму.
Приклад 2.
y = (x+1)2 (x-2)3
1) y/ = 2(x+1)(x-2)3 + (x+1)2 3(x-2)2 = (x+1)(x-2)2 (2x - 4 + 3x + 3) =
= (x+1)(x – 2)2(5x-1)
2) y/ = 0
(x+1)(x – 2)2(5x-1) = 0
x1 = -1 x2 = 2 x3 = ![]()

+ - + +
-1 ![]() 2
2
y/ (-2) = 16 (-11)(-1) › 0
y/ (0) = 4 (-1)1 ‹ 0
y/ (1) = 1 4 2 › 0
y/ (3) = 1 14 4 › 0
x = -1 - точка максимума
x = ![]() - точка мінімума
- точка мінімума
x = 2 - не э точкою екстремума
Друге правило:
- Знаходимо похідну функції.
-
Шукаємо критичні точки функції, прирівнючи похідну до 0:
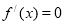
- Знаходимо похідну другого порядку.
-
Знаходимо значення похідної другого порядку в критичних точках. Якщо f // (x)
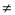 0 і f // (x)›0, то точка x є точкою мінімуму; якщо f // (x)
0 і f // (x)›0, то точка x є точкою мінімуму; якщо f // (x) 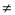 0 і f // (x)‹0, то точка x є точкою максимуму.
0 і f // (x)‹0, то точка x є точкою максимуму.
Приклад 3.
y = x3 – x2
1) y/ = 3x2 – 2x
2) y/ = 0
3x2 – 2x = 0
x1 = 0 x2 = ![]()
3) y // = 6x – 2
4) y // (0) = -2 ‹ 0, тоді x = 0 – точка максимуму
y // (![]() ) = 2 › 0, тоді x =
) = 2 › 0, тоді x = ![]() - точка мінімуму
- точка мінімуму
5. Закріплення вивченого матеріалу.
Дослідити функцію на зростання, спадання:
- y = x4 – 2x2 - 3
у/ = 4x3 - 4x
4x3 - 4x = 0
4x (x2 - 1) = 0
x1 = 0 x2 = 1 x3 = -1

-1 0 1 x
Функція спадає на (-![]() ; -1)
; -1)![]() (0;1), зростає на (-1; 0)
(0;1), зростає на (-1; 0)![]() (1;+
(1;+![]() ).
).
2)

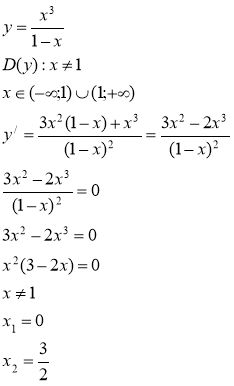
0 1 ![]() x
x
Функція зростає на (-![]() ;1)
;1)![]() (1;
(1;![]() ), спадає на (
), спадає на (![]() ;+
;+![]() ).
).
3)
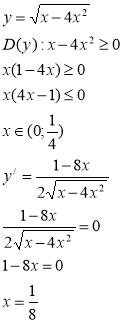
![]()
![]()
![]()
![]()
![]()
0 ![]()
![]()
Функція зростає на (0;![]() ), спадає на (
), спадає на (![]() ;
;![]() ).
).
2. Знайти екстремальні точки за першим і другим правилами:
1) ![]()
І спосіб
D(y): x![]() 0
0
y/ = 1- ![]()
![]()
1- ![]()
![]() = 0
= 0
![]()
x2 – 1 = 0
x1 = 1 x2 = -1

+ _ _ +
-1 0 1
x = -1 – точка максимуму
x = 0 – не є екстремальною точкою
x = 1 – точка мінімуму
ІІ спосіб
D(y): x![]() 0
0
y/ = 1- ![]()
![]()
1- ![]()
![]() = 0
= 0
![]()
x2 – 1 = 0
x1 = 1 x2 = -1
y// = ![]()
y // (1) = 2 › 0, тоді х = 1 є точкою мінімуму
y // (-1) = -2 ‹ 0, тоді х = 1 є точкою максимуму
2) y = 4x2 – x4
y/ = 8x – 4x3
8x – 4x3 = 0
-4x (x2 – 2) = 0
x1 = 0 x2 = ![]() x3 = -
x3 = - ![]()

+ _ + _
- ![]() 0
0 ![]()
x = - ![]() - точка максимуму
- точка максимуму
x = 0 - точка мінімуму
x = ![]() - точка максимуму
- точка максимуму
ІІ спосіб
y/ = 8x – 4x3
8x – 4x3 = 0
-4x (x2 – 2) = 0
x1 = 0 x2 = ![]() x3 = -
x3 = - ![]()
y // = 8 – 12x2
y //(0) = 8 › 0, тоді х = 0 – точка мінімуму
y //( ![]() ) = 8 – 12*2 = 8 – 24 ‹ 0, тоді х =
) = 8 – 12*2 = 8 – 24 ‹ 0, тоді х = ![]() - точка максимуму
- точка максимуму
y //( -![]() ) = 8 – 24 ‹ 0, тоді х = -
) = 8 – 24 ‹ 0, тоді х = - ![]() - точка максимуму
- точка максимуму
6. Підведення підсумків.
Отже, яку тему ми сьогодні вивчали?
Скільки екстремальних точок може мати функція?
Коли функція зростає (спадає)?
Як знайти екстремальні точки функції?
Яким правилом вам зручніше користуватись?
7. Домашнє завдання.
Алгебра і початки аналізу. Профільний рівень. 10 клас Мерзляк А.Г.
№40.7(1,2), №40.11 (1,2*).


про публікацію авторської розробки
Додати розробку
