Урок на тему "Ділення з остачею. Конгруенції та їх властивості"

Цикл уроків з алгебри на тему «Основи теорії подільності»

для 8 класів з поглибленим вивченням математики 

                підготувала вчитель математики

 НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів  - гімназія

 Дем´янюк Ганна Володимирівна

Урок №4

Тема: Ділення з остачею. Конгруенції та їх властивості

Мета: Вдосконалити вміння учнів знаходити неповну частку та остачу, оперувати з конгруенціями; розвивати розумові операції, вміння аналізувати, порівнювати, узагальнювати, класифікувати, розмірковувати за аналогією; виховувати самостійність, організованість і мотиви діяльності.

Тип уроку: урок формування навичок і вмінь

Обладнання: підручник, картки

Хід уроку:

1. Актуалізація опорних знань

(«Мозковий штурм»)

• Сформулюйте теорему про ділення з остачею.
• Яку властивість має різниця цілих чисел a і b. Які при діленні на натуральне число m дають однакові остачі?
• Яку властивість мають остачі при діленні цілих чисел   a і b на натуральне число   m,  якщо ?
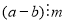• Які числа називають конгруентними за модулем m, де ?
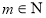• Сформулюйте необхідну й достатню умову того, що цілі числа  a і b конгруентні за модулем m, де .
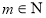• Сформулюйте властивості конгруенцій

2. Розв’язування вправ

  - розв’язування біля дошки з обговоренням, обміном думками, пропозиціями.

1) Непарне число m ділиться націло на 3. Чому дорівнює остача при діленні числа m на 6?

Розв’язання: при діленні цілого числа на 6 можуть бути отримані остачі 0,1,2,3,4,5. Тому будь-яке ціле число можна подати в одному з таких виглядів: .

З цих чисел кратні 3 тільки числа виду . Оскільки число m непарне,то воно може бути тільки виду . Отже, число m при діленні на 6 дає в остачі 3.

2. Доведіть, що серед п’яти послідовних цілих чисел є тільки одне, яке

кратне 5.

Розв’язання. Розглянемо п’ять послідовних цілих чисел: . Оскільки модуль різниці будь-яких двох таких чисел менший від 5 і не дорівнює нулю,то він не ділиться націло на 6. Отже, усі ці п’ять чисел дають різні остачі при діленні на 5. Різних остач при діленні на 5 також 5. Отже, одне з цих чисел при діленні на 5 дає остачу 0.

Міркуючи аналогічно, можна довести, що серед m послідовних цілих чисел є тільки одне, яке кратне m.

3)  Чому може дорівнювати остача при діленні числа на 5, де ?

Розв’язання: Має місце одна з п’яти конгруенцій: , , , , . Піднесемо обидві частини кожної з цих конгруенцій до четвертого степеня: , , , , . Отже, при діленні числа на 5 в остачі можуть бути отримані тільки числа 0 і 1.

4) Доведіть, що при будь-якому натуральному n значення виразу

  кратне 7.

Розв’язання: Маємо: . Очевидно, що . Застосовуючи послідовно властивості конгруенцій, запишемо:

, , , . Права частина останньої конгруенції при діленні на 7 дає в остачі 0. Отже, така властивість притаманна й лівій частині конгруенції.

5) Знайдіть остачу від ділення числа 7²⁹ на 5.

Розв’язання: Задача зводиться до того, щоб знайти ціле число х, яке задовольняє дві умови6: і . Маємо: , , .Отже, шукане число 2.

• робота в групах

1) Доведіть,  що остача при діленні на 3 квадрата цілого числа може дорівнювати тільки 0 або   1.

2) Чому може дорівнювати остача при діленні числа m³ на 7?

3)  Відомо, що (a²+b²)3. Доведіть, що  (a²+b²)9.

4) Використовуючи конгруенції, доведіть, що при будь-якому натуральному значенні n значення виразу: 1)11ⁿ+14*6ⁿ кратне 5;

  2)5²ⁿ⁺¹+2ⁿ⁺⁴+2ⁿ⁺¹ кратне 23;   3) 3²ⁿ+11*5ⁿ кратне 4

5) Знайдіть остачу від ділення числа а на b, якщо   a=5⁹⁹,b=3;

 3. Домашня робота

1) Чи існує ціле числа, яке при діленні на 6 дає остачу 4, а при діленні

 на 9 остачу 5?

2) Доведіть, що квадрат непарного числа при діленні на 8 дає в остачі 1.

3) Чому може дорівнювати остача при діленні числа k³ на 9?

4) Відомо, що (m²+n²)7. Доведіть, що  (m²+n²)49.

5) Використовуючи конгруенції, доведіть, що при будь-якому натуральному значенні n  значення виразу:

  1)17ⁿ+25*4ⁿ кратне 13;                                        4)6²ⁿ+3ⁿ⁺²+3ⁿ кратне 11;

  2)16ⁿ+4²ⁿ⁺¹ кратне 5;                                             5)17*21²ⁿ⁺¹+9*43²ⁿ⁺¹ кратне 8;

 3)15ⁿ+2³ⁿ-30 кратне 7;                                            6)2⁵ⁿ⁺³+5ⁿ*3ⁿ⁺² кратне 17;

Використані джерела:

1. Алгебра підручник для 8 класу з поглибленим вивченням математики,

А.Г. Мерзляк,  В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009

2. Алгебра та початки аналізу 10 клас, профільний рівень

А.Г. Мерзляк, Д.А. Номіровський,  В.Б. Полонський, М.С. Якір, - Харків «Гімназія», - 2010

3. О.Ю. Карік, Матеріали для факультативних занять, спецкурсів, гуртків, математика 5-7, Харків, - «Основа», -  2008