Алгоритми дій при розв'язувані деяких задач

Алгоритм дій під час скорочення звичайних дробів

1. Розкладіть чисельник на прості множники.
2. Розкладіть знаменник на прості множники.
3. Виділіть спільний дільник, відмінний від 1, для чисельника і знаменника.
4. Поділіть чисельник і знаменник на цей спільний дільник.

Алгоритм дій під час розв’язування нерівностей методом інтервалів

1. Зведіть нерівність до вигляду  f(x) < (>) 0.
2. Знайдіть область визначення функції.
3. Знайдіть нулі функції.
4. На числовій прямій позначте область визначення функції.
5. На позначеній  на прямій   області визначення функції  нанесіть нулі функції.
6. Дослідіть знак функції у кожному з отриманих інтервалів. Можна починати з крайнього правого інтервалу. Знак на цьому проміжку такий же, як і знак старшого коефіцієнта. Далі йде чергування знаків, якщо всі корені не парної кратності.
7.  Запишіть відповідь.

Алгоритм дій під час знаходження найбільшого  і     найменшого значення функції         на відрізку.

1. Переконайтеся, що заданий відрізок  входить до області визначення функції.
2. Знайдіть похідну функції.
3. Знайдіть критичні точки:     f ' (x) = 0,  або f ' (x)  не існує.
4. Виберіть критичні точки, які належать заданому відрізку.
5. Обчисліть значення функції в цих критичних точках і на кінцях цього відрізка.
6. Порівняйте одержані значення функції і виберіть із них найбільше і найменше.
7. Запишіть відповідь.

Алгоритм розв’язування раціонального     рівняння.   .

  1.     Переносимо доданки з правої частини рівняння у ліву.

  2.     Зводимо всі доданки лівої частини до спільного знаменника.

  3.     Спрощуємо.

  4.     Складаємо систему користуючись правилом:

       дріб дорівнює 0, тоді, коли чисельник дорівнює 0,

а знаменник  не дорівнює 0.

Алгоритм  розв’язування повних квадратних рівнянь за формулою

                                    ax²+bx+c=0

1.  Обчислити дискримінант  квадратного рівняння           

                                     D = b²—4ac

• Якщо   D>0 , то  =     =

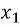• Якщо   D=0 , то  =

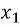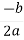
• Якщо   D<0, то   коренів немає