Арифметичний квадратний корінь з добутку, дробу, степеня
Тема. Арифметичний квадратний корінь з добутку, дробу, степеня
Мета: поглибити знання учнів про властивості арифметичного квадратного кореня, вивчені на попередньому уроці, знаннями про властивість квадратного кореня з парного степеня; сформувати вміння відтворювати вивчену властивість, а також застосовувати її для перетворення виразів, що містять арифметичний квадратний корінь як для виразів виду ![]() , так і для перетворення виразів із застосуванням властивостей квадратного кореня з добутку та квадратного кореня з частки.
, так і для перетворення виразів із застосуванням властивостей квадратного кореня з добутку та квадратного кореня з частки.
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Арифметичний квадратний корінь та його властивості».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
З метою ефективної перевірки засвоєння учнями матеріалу попереднього уроку роботу учнів на цьому етапі уроку можна організувати у вигляді виконання тестових завдань, що за змістом подібні до вправ домашньої роботи, або провести перевірку виконання домашнього завдання за зразком.
Тестове завдання
Яка з рівностей є правильною?
а) 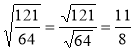 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) 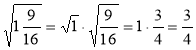 .
.
III. Формулювання мети і завдань уроку
З метою створення мотивації навчальної діяльності учнів на уроці після перевірки виконання домашнього завдання (і відповідно до повторення матеріалу попереднього уроку) вчитель створює проблемну ситуацію — пропонує учням виконати завдання:
Не використовуючи калькулятора та довідкового матеріалу, знайдіть значення виразів:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Спроби розв'язати завдання із використанням означення арифметичного квадратного кореня або властивостей, вивчених на попередньому уроці, не дають жодного результату. Це приводить учнів до усвідомлення існуючого протиріччя між знаннями та вміннями й тими завданнями, що постали перед ними.
Вивчення таких властивостей арифметичного квадратного кореня, що дадуть можливість упоратись із запропонованим завданням, та опанування способів їх застосування вкупі із вивченими на попередньому уроці властивостями - це і є основною метою уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати знання і вміння учнів такі: означення арифметичного квадратного кореня та його застосування для добування квадратного кореня з числа; властивостей степеня з натуральним показником (зокрема степінь степеня); застосування властивостей квадратного кореня з добутку та квадратного кореня з частки (відношення); означення модуля дійсного числа; розкладання цілого числа на прості множники.
Виконання усних вправ
- Чи правильна рівність:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
- Знайдіть значення виразів:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
- Вставте пропущений вираз: а ≥ 0; b >0
![]() ;
; 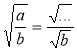 ;
; ![]() ;
; 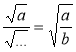 .
.
-
Обчисліть: |-5|; |-2,42|;
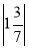 ; |0|.
; |0|.
- Спростіть: |-а6|; |х2|; |-у2 – 1|; |х – 1|.
V. Засвоєння знань
План вивчення нового матеріалу
-
Формулювання і доведення тотожності
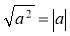 та
та 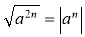 .
.
- Приклади застосування доведених тотожностей.
Опорними для тотожностей, винесених для вивчення на уроці, є означення арифметичного квадратного кореня з числа, основна тотожність для квадратного кореня та означення модуля дійсного числа. Доведення тотожності ведеться за тією самою схемою, що й доведення властивостей квадратного кореня з добутку та квадратного кореня з частки, але для кращого розуміння учнями можна розбити цю тотожність на два випадки: окремо довести її для випадку, якщо а ≥ 0 (останнім часом у загальноосвітній школі доводили тільки цю частину тотожності), а потім довести її для випадку, якщо а ≤ 0 (а < 0).
Закінчити вивчення нового матеріалу уроку логічно було б розв'язуванням прикладів, запропонованих учням на етапі формулювання мети уроку, показавши переваги застосування вивченої тотожності та властивостей, вивчених на попередньому уроці. Ці вправи записуються в зошити учнів як опорні приклади. Звернімо увагу учнів на те, що в обчисленні квадратного кореня з добутку кількох натуральних чисел доцільно розкладати множники в підкореневому виразі на прості множники та працювати з добутком степенів простих чисел. Серед вправ, що запропоновані як опорні, слід розглянути також вправи на спрощення виразів, що мають вигляд ![]() , де А — деякий раціональний вираз; під час розв'язування такого завдання слід одразу зробити акцент (і надалі постійно звертати увагу учнів) на тому, що в застосуванні вивченої на уроці тотожності обов'язково слід визначити знак виразу А.
, де А — деякий раціональний вираз; під час розв'язування такого завдання слід одразу зробити акцент (і надалі постійно звертати увагу учнів) на тому, що в застосуванні вивченої на уроці тотожності обов'язково слід визначити знак виразу А.
VI. Формування вмінь
Виконання усних вправ
-
Обчисліть значення виразу:
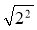 ;
; 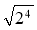 ;
; 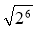 ;
; 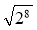 .
.
-
Обчисліть:
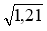 ;
; 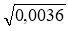 ;
; 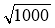 ;
; 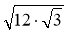 ;
; 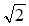 ·
·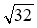 ;
; 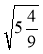 ;
; 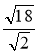 ;
; 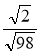 ;
; 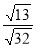 ;
; 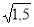 ·
·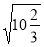 ;
; 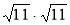 .
.
-
Спростіть:
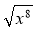 ;
; 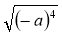 ;
; 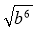 при b ≥ 0;
при b ≥ 0; 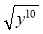 при у ≤ 0.
при у ≤ 0.
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту:
- Знаходження значення числового виразу, що має вигляд арифметичного квадратного кореня з квадрата дійсного числа.
Обчисліть: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж) 2
; ж) 2![]() ; з) 5
; з) 5![]() ; и) 0,2
; и) 0,2![]() .
.
-
Знаходження значень виразів, що містять корінь з парного степеня
дійсного числа.
1) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2) Знайдіть значення виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3) Обчисліть значення виразу (якщо воно має зміст):
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
4) Обчисліть: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
-
Знаходження значень виразів, що мають вигляд кореня з добутку
або частки чисел, які потребують попереднього розкладання на
прості множники.
1) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
-
Спрощення виразів, які мають вигляд квадратного кореня з квадра
та або парного степеня раціонального виразу (або можуть бути по
дані в такому вигляді після виконання тотожних перетворень).
1) Замініть вираз тотожно рівним:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
2) Спростіть вираз: а) ![]() , де у ≥ 0; б)
, де у ≥ 0; б) ![]() ; в)
; в) ![]() , де х < 0;
, де х < 0;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() , де t < 0.
, де t < 0.
3) Виконайте перетворення виразу:
а) ![]() , де х < 0; б)
, де х < 0; б) ![]() , де а ≥ 0; в)
, де а ≥ 0; в) ![]() ; г)
; г) ![]() .
.
4) Спростіть вираз:
а) ![]() , де а ≥ 0, b ≥ 0; б)
, де а ≥ 0, b ≥ 0; б) ![]() , де а ≥ 0, b ≤ 0;
, де а ≥ 0, b ≤ 0;
в) ![]() , де у < 0; г)
, де у < 0; г) 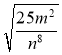 , де т ≥ 0; д)
, де т ≥ 0; д) ![]() , де а < 0;
, де а < 0;
є) ![]() , де х > 0, у < 0.
, де х > 0, у < 0.
-
Логічні вправи та завдання вищого рівня складності для учнів, які
мають достатній та високий рівні знань.
1) При яких значеннях а і натуральних значеннях п є правильною рівність ![]() ?
?
2) При яких значеннях х є правильною рівність:
a) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ?
?
3) Знайдіть пропущений вираз
|
|
|
|
|
|
|
? |
- На повторення: розв'язати завдання на застосування вивчених на попередньому уроці властивостей квадратного кореня. Обчисліть:
а) ![]() ; б)
; б) ![]() ; в)
; в) 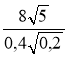 ; г)
; г) 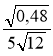 .
.
На уроці продовжується робота з формування вмінь учнів застосовувати вивчені властивості арифметичного квадратного кореня для обчислення значень числових виразів раціональним способом (без-застосування калькулятора та довідкових таблиць). Крім того розпочинається підготовча робота перед вивченням наступної теми «Тотожні перетворення виразів, що містять арифметичний квадратний корінь», а саме робота з підготовки учнів до сприйняття такого поняття, як винесення множника з-під знака кореня.
VI. Підсумки уроку
В якому з випадків правильно виконано дію?
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() , г) a ≤ 0,
, г) a ≤ 0, ![]() .
.
VII. Домашнє завдання
- Вивчити формулювання і способи застосування властивостей арифметичного квадратного кореня, розглянутих на уроках 38, 39.
- Виконати вправи на застосування цих властивостей (змісту, аналогічного до вправ класної роботи).
- Повторити означення арифметичного квадратного кореня з числа, схему розв'язання рівняння х2 = а, а також співвідношення між відомими учням числовими множинами та означення чисел, що входять до кожної з вивчених множин.


про публікацію авторської розробки
Додати розробку
