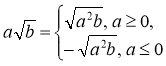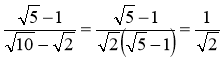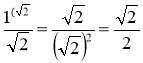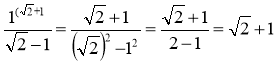Винесення множника з-під знака кореня, внесення множника під знак кореня
Тема 2. Квадратні корені
Урок № 41
Тема. Винесення множника з-під знака кореня, внесення множника під знак кореня
Мета: домогтися засвоєння учнями змісту алгоритму перетворення, що має назву винесення множника з-під знака кореня та змісту алгоритму перетворення, що має назву внесення множника під знак кореня; сформувати вміння учнів виконувати названі перетворення за вивченими алгоритмами, а також застосовувати ці перетворення в розв'язуванні вправ на тотожні перетворення цілих ірраціональних виразів.
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Перетворення ірраціональних виразів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Зібрати зошити учнів для перевірки якості виконання письмової частини домашнього завдання (у тому числі й самостійної роботи).
III. Формулювання мети і завдань уроку
На початку вивчення цього розділу вчитель повідомляє учням про те, що вивчені означення та властивості арифметичного квадратного кореня можуть бути використані для перетворення деяких видів виразів, що містять квадратні корені. З кількома з таких видів перетворень учні мають познайомитись на поточному уроці.
З метою усвідомлення учнями необхідності вивчення матеріалу уроку можна на етапі формулювання мети запропонувати виконати завдання, в результаті чого вони дійдуть розуміння певної проблеми, яку слід розв'язати на уроці.
Завдання 1
Порівняйте значення виразів ![]() і
і ![]() .
.
Завдання 2
Порівняйте значення виразів ![]() і
і ![]() .
.
Завдання 3
Порівняйте значення виразів ![]() і
і ![]() .
.
Якщо з виконанням першого і другого завдань в учнів не виникає проблем (у неявному вигляді застосовується властивість монотонності функції у = х2 на проміжку [0; ∞)), то з третім завданням швидше за все учні не впораються (слід нагадати, що, виконуючи дії з коренями, слід спиратись тільки на вивчені властивості, не вигадуючи неіснуючих властивостей). Порівнявши всі завдання, учні доходять висновку про необхідність оволодіння такими способами дій, що дозволять переходити під час розв'язування вправ, подібних до запропонованих, від «незручних» записів виразів, що містять корені, до «зручних». Таким чином формулюється основна дидактична мета уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття нового матеріалу слід активізувати такі знання і вміння учнів: означення, властивості та основна тотожність для арифметичного квадратного кореня з числа; тотожні перетворення цілих раціональних виразів, а також виконання арифметичних дій з раціональними числами.
Виконання усних вправ
-
Знайдіть значення виразів:
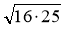 ;
; 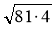 ;
; 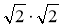 ;
; 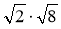 ;
; 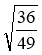 ;
; 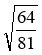 ;
; 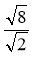 ;
; 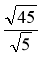 ;
; 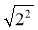 ;
; 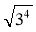 ;
; 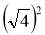 ;
; 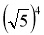 .
.
-
Подайте у вигляді
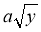 вирази:
вирази: 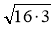 ;
; 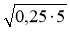 ;
; 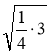 ;
; 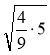 .
.
-
Спростіть вираз: а) 3а – 2а + 5а; б) (а – 2)(а + 3); в) (а – 2);
г) (а + 3)2; д) (а – 3)(а + 3); є) (а – 1)2 + 2а; ж)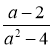 ; з)
; з) 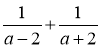 .
.
V. Засвоєння знань
План вивчення нового матеріалу
- Що означає винести множник з-під знака кореня? Як винести множник з-під знака кореня в числовому та буквеному виразах?
- Що означає внести множник під знак кореня? Як внести множник під знак кореня в числовому та буквеному виразах?
- В яких завданнях можна застосовувати ці перетворення? (Зразки завдань).
|
Конспект 11 |
||
|
Перетворення ірраціональних виразів |
||
|
1. Винесення множника з-під знака кореня. |
||
|
|
Якщо b ≥ 0, то |
|
|
2. Внесення множника під знак кореня. |
||
|
|
Якщо b ≥ 0, то |
|
|
3. Арифметичні дії з виразами, що містять арифметичний квадратний корінь. |
||
|
а) Алгебраїчне додавання: |
||
|
б) множення: |
||
|
|
||
|
|
||
|
в) ділення: |
||
|
г) позбавлення від ірраціональності в знаменнику дробу: |
||
|
|
||
Перетворення, що називаються винесенням множника з-під знака кореня та внесенням множника під знак кореня, ґрунтуються на властивості квадратного кореня з добутку та властивості ![]() . Зазвичай під час вивчення цих перетворень у 8 класі не формулюються спеціальні правила виконання вказаних перетворень (способи дій на рівні тотожностей узагальнюються пізніше, під час вивчення кореня n-го степеня та його властивостей), схема перетворень пояснюється на конкретних прикладах. Вивчені попередні теми (означення, властивості та основна тотожність для квадратного кореня) достатньо підготували учнів до сприйняття нової теми. Тому у вивченні нового матеріалу використовуємо пошукові методи роботи: учитель формулює завдання знайти два різні способи розв'язання проблемної ситуації, що виникла на етапі формулювання мети (ці два способи відповідають умові першого і другого завдань). Порівнявши вид записів виразів у першому і другому завданнях, можна запропонувати самим учням (нагадавши їм ще раз, що проблема розв'язується незвичним застосуванням вивчених властивостей арифметичного квадратного кореня) знайти ці способи. Далі, порівнявши спосіб перетворень та вид здобутих після їх виконання виразів, учні мають усвідомити, що назва кожного перетворення відображає його зміст. Після цього вчитель формулює опис кожного з розглянутих перетворень та ще раз, розглянувши приклади виконання кожного перетворення, дає детальний коментар до кожного з них.
. Зазвичай під час вивчення цих перетворень у 8 класі не формулюються спеціальні правила виконання вказаних перетворень (способи дій на рівні тотожностей узагальнюються пізніше, під час вивчення кореня n-го степеня та його властивостей), схема перетворень пояснюється на конкретних прикладах. Вивчені попередні теми (означення, властивості та основна тотожність для квадратного кореня) достатньо підготували учнів до сприйняття нової теми. Тому у вивченні нового матеріалу використовуємо пошукові методи роботи: учитель формулює завдання знайти два різні способи розв'язання проблемної ситуації, що виникла на етапі формулювання мети (ці два способи відповідають умові першого і другого завдань). Порівнявши вид записів виразів у першому і другому завданнях, можна запропонувати самим учням (нагадавши їм ще раз, що проблема розв'язується незвичним застосуванням вивчених властивостей арифметичного квадратного кореня) знайти ці способи. Далі, порівнявши спосіб перетворень та вид здобутих після їх виконання виразів, учні мають усвідомити, що назва кожного перетворення відображає його зміст. Після цього вчитель формулює опис кожного з розглянутих перетворень та ще раз, розглянувши приклади виконання кожного перетворення, дає детальний коментар до кожного з них.
Також важливо на уроці розглянути завдання на застосування вивчених перетворень для виконання порівняння виразів, що містять арифметичний квадратний корінь. Розв'язані приклади завдань учні мають записати в зошити як опорні приклади.
VI. Формування вмінь
Виконання усних вправ
-
Спростіть вираз: а)
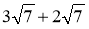 ; б)
; б) 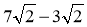 ; в)
; в) 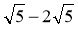 ; г)
; г) 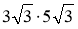 ; д)
; д) 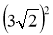 ; є)
; є) 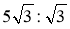 .
.
- Закінчіть розкладання на множники:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ; г)
; г) ![]()
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту:
- Внесення (винесення) числового додатного множника під знак (з-під знака) кореня.
1) Винесіть множник з-під знака кореня: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
2) Внесіть множник під знак кореня:
а) 3![]() ; б) 4
; б) 4![]() ; в) 2
; в) 2![]() ; г) 9
; г) 9![]() ; д) 4
; д) 4![]() ; є) 0,1
; є) 0,1![]() ; ж) 2
; ж) 2![]() ; з)
; з) ![]() .
.
-
Внесення (винесення) буквеного додатного множника під знак
(з-під знака) кореня.
1) Винесіть множник з-під знака кореня: а) ![]() , де х ≥ 0;
, де х ≥ 0;
б) ![]() , де у ≤ 0; в)
, де у ≤ 0; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Винесіть множник з-під знака кореня: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() , де х ≤ 0; г)
, де х ≤ 0; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() , де с < 0.
, де с < 0.
3) Внесіть множник під знак кореня:
а) ![]() , де а ≥ 0; б)
, де а ≥ 0; б) ![]() ; в)
; в) ![]() .
.
- Порівняння значень ірраціональних виразів.
1) Порівняйте значення виразів:
а) 3![]() і
і ![]() ; б)
; б) ![]() і 3
і 3![]() ; в) 5
; в) 5![]() і 4
і 4![]() ; г) 2
; г) 2![]() і 3
і 3![]() .
.
2) Порівняйте значення виразів: а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ;
;
в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() .
.
- Розташування ірраціональних чисел у порядку зростання (спадання). Розташуйте в порядку зростання числа:
а) 3![]() , 2
, 2![]() ,
, ![]() , 4
, 4![]() ; б) 6
; б) 6![]() ,
, ![]() , 3
, 3![]() , 2
, 2![]() .
.
- Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Винесіть множник з-під знака кореня:
а) ![]() , де а < 0; б)
, де а < 0; б) ![]() , де а > 0; в)
, де а > 0; в) ![]() , де а ≤ 0, b ≤ 0;
, де а ≤ 0, b ≤ 0;
г) ![]() ; д)
; д) ![]() ; с)
; с) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
2) Який вираз пропущено?
|
|
|
|
3 |
? |
- На повторення: завдання на перетворення раціональних (цілих та дробових) виразів.
1) Спростіть вираз: а) 3(2х – 1) – 2(х + 5); б) (3х + 5)2 + (2 – 3х)(2 + 3х);
в) 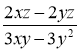 ; г)
; г) 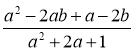 .
.
2) Розкладіть на множники:
а) 8х2у3 – 12х3у; б) 3a + 6b – ca – 2cb; в) (а – b)2 – 2(а2 – b2); г) 8m3 – 27.
3) Чи може значення виразу 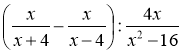 дорівнювати 1?
дорівнювати 1?
Завдання, запропоновані для розв'язування на уроці, можна умовно поділити на дві групи: завдання, в яких прямо говориться про необхідність виконання перетворення — внести (винести) множник під знак (з-під знака) кореня, та завдання, в яких перетворення прямо не називається (учні самі мають вибрати, яке перетворення вони можуть застосувати). Підготовчими для вивчення наступної теми є завдання на повторення: перетворення раціональних виразів.
VII. Підсумки уроку
В якому з випадків правильно виконано дію?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
VIII. Домашнє завдання
- Вивчити теоретичний матеріал уроку.
- Розв'язати вправи на закріплення оперативних умінь, сформованих на уроці.
- На повторення: правила виконання дій з цілими виразами (з одночленами, многочленами — довідник, 7 клас); вправи на застосування повторених правил.
1
С.П.Бабенко Усі уроки алгебри 8 клас Урок № 41


про публікацію авторської розробки
Додати розробку