Тотожні перетворення виразів, що містять квадратний корінь

Урок № 42

Тема.  Тотожні перетворення виразів, що містять квадратний корінь

Мета: домогтися засвоєння учнями схем виконання дій під час пе­ретворення цілих виразів, що містять квадратний корінь; сформувати вміння застосовувати вивчені схеми для розв'язування завдань на пе­ретворення виразів, що містять квадратний корінь, які відповідають вимогам чинної програми з математики.

Тип уроку: застосування знань, умінь та навичок.

Наочність та обладнання: опорний конспект «Перетворення ірра­ціональних виразів».

Хід уроку

I. Організаційний етан

II. Перевірка домашнього завдання

Вчитель організує роботу у формі «Знайди помилку», запропону­вавши учням для перевірки варіанти виконання письмових вправ до­машнього завдання з «допущеними помилками» (для зручності ці розв'язання виконані у формі роздавального матеріалу). По закінченні виконання роботи учні перевіряють правильність виконання «пе­ревірки», отримавши на руки правильні розв'язання. У разі не­обхідності складні та спірні моменти обговорюються.

III. Формулювання мети і завдань уроку

З метою усвідомлення учнями необхідності вивчення матеріалу уроку можна на етапі формулювання мети запропонувати виконати за­вдання, в результаті чого учні дійдуть розуміння проблеми, яку не­обхідно розв'язати на уроці.

Завдання 1

Виконайте дії: 12а + 4а; (a – 1)(a + 1); (1 + 2а)(2 – а) + 3а.

Завдання 2

Виконайте дії: ; ; .

Якщо з розв'язанням першого завдання в учнів проблем не ви­никає, то з другим завданням швидше за все учні не впораються (слід нагадати учням, що, виконуючи дії з коренями, слід спиратись тільки на вивчені властивості та схеми дій). Тому, порівнявши обидва завдан­ня, учні доходять висновку про недостатність знань щодо означення та властивостей арифметичного квадратного кореня, вивчених на попе­редніх уроках; учні мають усвідомити необхідність оволодіння такими способами дій, що дозволять, використовуючи вивчені властивості квадратного кореня та вміння перетворювати раціональні вирази, ви­конувати перетворення виразів, що містять корені.

Таким чином формулюється основна дидактична мета уроку.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття навчального матеріалу слід акти­візувати такі знання і вміння учнів: первинні вміння виносити множник з-під знака кореня та вносити множник під знак коре­ня; виконання тотожних перетворень цілих раціональних виразів; застосування основної тотожності для квадратного кореня.

Виконання усних вправ

1. Знайдіть значення виразу: ; ; ; ; ; ; ; ; ; .
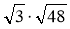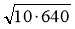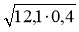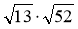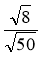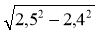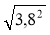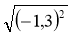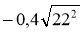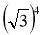2. Подайте у вигляді 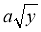вираз: ; ; ; .
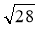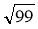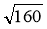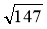3. Спростіть вираз: а) 3а + 2а + 5а; б) (а + 2)(а + 3); в) (а + 2) ; г) (а + 3)²;

д) (а – 3)(а + 3); є) (а – 1)² + 2а; є) ; ж) .

V. Застосування знань

 Насправді на уроці не вивчаються нові теоретичні положення: увесь зміст нового матеріалу представлений опорними прикла­дами розв'язування завдань на перетворення цілих виразів, що містять арифметичний квадратний корінь. Тому план вивчення матеріалу уроку являє собою фактично опис змісту виразів, способи перетворення яких мають опанувати учні на уроці:

• вирази, що мають вигляд многочлена (наприклад, 12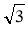+ 4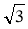), та такі, що зводяться до них шляхом винесення множника з-під знака кореня;
• вирази, що мають вигляд добутку (степеня) одночленів; добутку од­ночлена на многочлен або многочлена на многочлен;
• вирази, що містять усі названі дії та мають степені сум виразів із квадратними коренями;
• окремо виділяємо вирази, в яких слід виконати розкладання на множники.

У роботі над вивченням способів дій за перетворення названих ви­разів дуже доречно буде використовувати аналогію — для кращого ро­зуміння учнями змісту перетворень запропонувати виконати записи у вигляді порівняльної таблиці, в якій розглянути спочатку приклад на перетворення цілого раціонального виразу, а потім приклад на відпо­відне перетворення цілого ірраціонального виразу (виразу, що містить квадратний корінь). Ця таблиця може мати такий вигляд:

І так далі...

VI. Формування вмінь

Виконання усних вправ

1. Спростіть вираз:

а) ; б);  в) ;

г) .

2. Розкладіть на множники:

а) ; б); в) с² – 2; г); д); є) .

Виконання письмових вправ

Для реалізації дидактичної мети уроку на цьому уроці слід розв'я­зати завдання такого змісту:

1. Додавання (віднімання) виразів, що містять арифметичний квад­ратний корінь.

1) Спростіть вираз: а) ; б) ; в) ;

 г) ; д) ; є) .

2) Спростіть вираз: а) ; б) ;

 в) ; г) .

3) Спростіть вираз: а) ; б) .

2. Множення та піднесення до степеня виразів, що містять арифме­тичний квадратний корінь.

1) Спростіть вираз:
а) ; б) ; в) ;

г) ; д) ; є) ; ж) ;

з) ; и) ; к) .

2) Спростіть вираз: а) ; б) ;

в) ; г) ; д) ;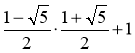

є) .

3) Спростіть вираз:
а) ; б) ;

в) ; г) .

3. Розкладання на множники виразів, що містять арифметичний
   квадратний корінь.

1) Розкладіть на множники.:

а) ; б) ; в) ; г) ; д) ;

є) ; ж) х² – 3; з) 5 – 4а²; и) х – 6, де х ≥ 0.

2) Розкладіть на множники вираз: а) ; б) ; в) ;

г) ; д) ; є) ; ж) ; з) .

4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Доведіть, що: а) ; б) .

2) Доведіть, що значення виразів

і

є натуральними числами.

3) Вставте пропущений вираз:

5. На повторення: завдання на перетворення дробових раціональних виразів. Спростіть вираз:

а) ;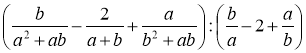

б) ;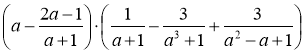

в) .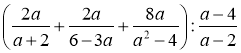

 Завдання, запропоновані для розв'язування на уроці, є досить складними для багатьох восьмикласників, оскільки потребують впевненого володіння об'ємним матеріалом: властивості квадрат­ного кореня, перетворення виразів, що містять корені (винесення множника з-під знака кореня та внесення множника під знак кореня), а також алгоритми перетворення цілих раціональних виразів, вивчені у 7 класі (дії з одночленами, многочленами, різні способи розкладання цілих виразів на множники). Тому, з метою свідомого виконання дій, тобто для уникнення по­милок, під час розв'язування завдань слід вимагати від учнів коменту­вати свої дії. При цьому бажано, щоб учні починали виконувати за­вдання зі з'ясування того, які дії слід обирати за умовою завдання; а потім уже визначали порядок дій та .виконували ці дії у встановлено­му порядку. Зрозуміло, що розпочинати формування вмінь учнів слід на найпростіших прикладах, поступово (якщо учні вдало опановують матеріал) підвищуючи рівень складності завдань.

VII. Підсумки уроку

В якому з випадків правильно виконано дію?

а) ; б) ;

в) ; г) .

VIII. Домашнє завдання

1. Вивчити теоретичний матеріал уроку.
2. Розв'язати вправи на закріплення оперативних умінь, сформованих на уроці.
3. На повторення: правила виконання дій з дробовими раціональни­ми виразами (див. розділ І, 8 клас); вправи на застосування повто­рених правил.