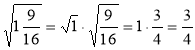Арифметичний квадратний корінь з добутку, дробу, степеня.

Тема. Властивості арифметичного квадратного кореня

Мета:

поглибити знання учнів про властивості арифметичного квадратного кореня, вивчені на попередньому уроці; сформувати вміння застосовувати дані властивості для перетворення  виразів, що містять арифметичний квадратний корінь як для виразів виду , так і для перетворення виразів із застосуванням властивостей квадратного кореня з добутку та квадратного кореня з частки;

стимулювання учнів до висловлювань без побоювань помилитися; формування компетентності спілкування державною мовою;

виховувати наполегливість, інтерес до пізнання нового.

Тип уроку: засвоєння знань та вмінь.

Обладнання  та наочність: конспект уроку,  кубик Блума, підручник А.Г. Мерзляк, ПК (телефон)  з інтернетом,  «Сlassroom», «Google Meet» .

Хід уроку

Учні класу Дитина з ООП

4. Засвоєння знань

Формулювання всіх властивостей

і 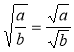(для а ≥ 0, b ≥ 0 та для       а ≥ 0 і b > 0), і .

Головним для тотожностей, винесених для вивчення на уроці, є означення арифметичного квадратного кореня з числа, основна тотожність для квадратного кореня та означення моду­ля дійсного числа.

Звернімо увагу учнів на те, що в обчис­ленні квадратного кореня з добутку кількох натуральних чисел доцільно розкладати множники в підкореневому виразі на прості множники та працювати з добутком степенів простих чисел.

Слід розглянути також вправи на спрощення ви­разів, що мають вигляд , де А — деякий раціональний вираз; під час розв'язування такого завдання слід одразу зробити акцент (і надалі постійно звертати увагу учнів) на тому, що в застосуванні вивченої на уроці тотожності обов'язково слід визначити знак виразу А.

5. Формування вмінь

5.3 Виконання додаткових вправ

Для реалізації дидактичної мети на уроці слід розв'язати за­вдання такого змісту:

1. Знаходження значення числового виразу, що має вигляд арифметичного квадратного кореня з квадрата дійсного числа.

Обчисліть: а) ; б) ; в) ; г) .

2. Знаходження значень виразів, що містять корінь з парного степеня
   дійсного числа.

 Знайдіть значення виразу: а) ; б) ; .

3.   Знаходження значень виразів, що мають вигляд кореня з добутку
   або частки чисел, які потребують попереднього розкладання на
   прості множники.

1) Знайдіть значення виразу: а) ; б) ; в) ; г) .

2) Знайдіть значення виразу: а) ; б) .

6. Підсумки уроку

6.1 Підсумкова бесіда

6.2 Оцінення учнів

7. Домашнє завдання

Повторити параграф 15, розв’язати 482, 488(1-3)