Біуроки. Зарубіжна література та математика.
Біуроки охоплюють матеріал 5-9 класів за новою програмою. Уроки проводять два вчителі – літератури та математики. Тривалість уроку – дві години. Теми біуроків вибрані так, щоб розширити рамки шкільної програми, зробити їх цікавими і змістовними. Мета і завдання таких пар – інтегрувати літературу і математику у цілісну структуру, зробити урок монолітним.
Федорова Людмила Валеріївна, вчитель зарубіжної літератури Ловінський Віктор Михайлович,
Передмова
Відомий спеціаліст в психолого-педагогічній науці В. П. Безпалько у своїй статті «Психологічні парадокси освіти» зазначає: «Пора зрозуміти уже очевидну істину, найвдаліше виражену у формулі А. В. Луначарського: «Кожна людина повинна засвоїти дещо про все і все про дещо»». Ознайомившись з останніми тенденціями в сучасному освітньому просторі, які на нашу думку і відображають формулу А. В. Луначарського, пропонуємо низку біуроків - зарубіжна література та математика. Такі уроки допоможуть вчителям у запровадженні культурологічного підходу до викладання предметів у школі, вміло інтерпретувати понятійним апаратом літератури та математики з метою розширення компетенцій учнів.
Біуроки охоплюють матеріал 5-9 класів за новою програмою. Уроки проводять два вчителі – літератури та математики. Тривалість уроку – дві години. Теми біуроків вибрані так, щоб розширити рамки шкільної програми, зробити їх цікавими і змістовними. Мета і завдання таких пар – інтегрувати літературу і математику у цілісну структуру, зробити урок монолітним.
Важливу роль у підвищенні ефективності біуроків відіграє його навчально-матеріальне та технічне оснащення. В конспектах ми намагалися акцентувати увагу на доцільності застосування мультимедійного та іншого обладнання, приділили увагу вигляду схем, таблиць, портретів, слайдів презентацій.
Біурок у 9 класі
Тема: Таємниця «Пікової дами» О. С. Пушкіна та теорія ймовірностей.
Мета: навчити учнів узагальнювати прочитане, робити висновки, удосконалювати навички роботи з текстом та математичними обчисленнями; розвивати зв’язне мовлення школярів, їх логічне та абстрактне мислення; виховувати творчість, вміння з користю організовувати свій вільний час.
Оформлення та обладнання класу: «гральний стіл» із колодами картами-
завданнями, гральними кубиками, монетами та підсвічником; колаж із зображенням «трійки»-Паскаль-Ферма-Пушкін, «сімки»-Лізи, «туза»-Лапласа, «пікової дами»-графині, «валета»-Германа; аудіо запис початку гри «Що? Де? Коли?», таблиця для обліку конкурсних балів.
Что ни толкуй Вольтер или Декарт, Мир для меня – колода карт.
Жизнь – банк, рок мечет, я – играю,
И правила игры я к людям применяю.
М. Ю. Лермонтов Хід уроку
I. Оголошення теми, мети, структури уроку.
II. Пролог – слово вчителя
Світова література
В XVIII-XIX ст. гра в карти стає невід’ємною частинною життя заможних верст суспільства в Європі. Гра в карти стає модою. Для одних – це забава, для інших – пристрасне захоплення. Про пристрасті, які вирували навколо гральних столів, про підступність Планиди і розповів у повісті «Пікова дама» О. С. Пушкін. Традиційно для творів, що розповідають про карточні ігри («Маскарад» М. Ю. Лермонтов, «Гравці» М.В. Гоголь, «Гравець» Ф. М. Достоєвський), сюжет твору насичений таємничим і містичним. Повість написана в манері Гофмана і Нодьє.
Карти асоціюються із ворожінням і передбаченням. А ці особливості завжди цікавили і зачаровували людську свідомість. Хто з нас не хотів би знати про своє майбутнє, хто з нас не гадав на Андрія чи Різдво? Математика
Хто з нас не хотів би навчитись передбачати результат гри?..
Кому з нас у повсякденні не доводиться оцінювати свої шанси на успіх у тій чи іншій ситуації?..
Мабуть, важко назвати в наш час людину освіченою, якщо вона, хоча б у загальних рисах, не чула про взаємозв’язок між «неминучим» і «випадковим»…
Виявляється, що існує наука, яка займається оцінкою настання того чи іншого. На перший погляд, в назві цієї науки об’єднані два несумісні слова: «теорія ймовірностей»…
Думаю, що питаннями теорії ймовірності переймався і О. С. Пушкін, бо як пояснити той факт, що перше популярне видання основ теорії ймовірностей з’явилося в Росії саме на сторінках «Современника» (журнал видавався О.Пушкіним; автором статей був П. Б. Козловський – високоосвічений дипломат). А його пристрасть до карт – це перевірка законів теорії ймовірностей. До чого може призвести така перевірка тих, хто не знайомий з її основами, – ось ще який підтекст захований у повісті О. С. Пушкіна «Пікова дама».
III. Енциклопедична пауза – «історичний» кон
Учні отримали випереджувальне завдання: знайти і підготувати доповіді про історію зародження теорії ймовірностей та історію написання О.С. Пушкіним повісті «Пікова дама» (див. додаток 1, 2); клас ділиться на дві команди: І – «цифра», ІІ – «герб»; підкидання монети визначає право першого ходу, а підкидання кубика – кількість балів за історичні екскурси; вчителі слідкують за логічним ходом відповідей та підраховують бали.
IV. Другий кон – «сюжетний»
Вчитель літератури
Кожна команда витягує з колоди по три карти-запитання за сюжетом повісті
(див. додаток 3); підкидання монети визначає право першого ходу, а підкидання кубика – кількість балів за відповідь на карту-запитання; вчитель літератури слідкує за логічним ходом відповідей, а вчитель математики підраховує бали
V. Третій кон – «понятійний апарат теорії ймовірностей»
Вчитель математики
Спробуємо оцінити шанси Германа на успіх, застосовуючи теорію ймовірностей. Для цього введемо основні її поняття.
Підкидання монети чи грального кубика називатимемо випробуванням. Результат випробування: випадання «герба» чи «цифри», витягування певної карти із колоди, випадання грані кубика із числом балів – елементарна подія. Для випробування, наприклад, підкидання грального кубика можливі такі елементарні події: випадання одиниці, двійки, трійки, четвірки, п’ятірки або шістки. Множину все можливих варіантів елементарної події назвемо
простором елементарних подій випробування. Якщо розглянути випробування підкидання монети, то зазвичай випадає або «герб», або «цифра» - вірогідна подія і ніколи не випаде «ребро» монети – неможлива подія. Підмножина простору елементарних подій називається подія. Наприклад, коли витягувати із колоди туза, то можливих варіантів є чотири (кількість тузів у колоді), тобто можливі чотири елементарні події: піковий туз, бубновий туз, червовий туз і хрестовий туз. Подія, яка під час випробування може як здійснитися, так і не здійснитися, називається випадковою.
Лаплас (поч. ХІХ ст.) – числова оцінка «вірогідної події» (класичне означення ймовірності)
m
n ,
де
Р(А) – ймовірність події А, m – число випадків події А, n – число усіх випробувань.
Спробуємо оцінити ймовірність випадання «герба» («цифри») при одноразовому підкиданні монети:
m1,n 2,P(A) 
0,5 50%.
А тепер оцінимо ймовірність витягування туза із колоди у 36 карт за перший раз:
m
4,n 36,P(A)
0,110% .
Як бачимо, ймовірність настання події у другому випадку порівняно з першим зменшилась у п’ять разів.
Щодо кількісної оцінки ймовірності виграшу Германа, то вона набагато порядків менша і залежить від кількості гравців та карт, що беруть участь у грі. Оцінити точніше його ймовірність виграти за допомогою класичного означення ми не зможемо, для цього існують більш складніші формули, які розглядатимемо у старших класах.
Натомість розглянемо цікаву задачу для любителів гри в кості: яка ймовірність випадання 9-ти очок при підкиданні двох кубиків одночасно? Розв’язання. m – 4;
|
грані |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
1\1 |
2\1 |
3\1 |
4\1 |
5\1 |
6\1 |
|
2 |
1\2 |
2\2 |
3\2 |
4\2 |
5\2 |
6\2 |
|
3 |
1\3 |
2\3 |
3\3 |
4\3 |
5\3 |
6/3 |
|
4 |
1\4 |
2\4 |
3\4 |
4\4 |
5/4 |
6\4 |
|
5 |
1\5 |
2\5 |
3\5 |
4\5 |
5\5 |
6\5 |
|
6 |
1\6 |
2\6 |
3\6 |
4\6 |
5\6 |
6\6 |
n – 36;
4 1
Р(А)=
- з
повтореннями.
36 9
VI. Четвертий кон - «задача Германа»
Вчитель математики
Для того, щоб оцінити, хоча б приблизно, ймовірність виграшу Германом, розглянемо таку задачу: знайти ймовірність випадання підряд «трійки», «сімки», «туза» із колоди у 52 карти з першого разу.
Розв’язання. Для знаходження числа випадків події: m P3!1236.
Для знаходження числа усіх випробувань:
n
C523 52!
1
2
3
...49 505152
505152
22100.
(523)!3! 1 2 3 ...49 6 6
Отже,
P(A) 
.
Перефразовуючи отриманий результат, можна сказати, що у Германа було шість шансів із двадцять двох тисяч ста можливих.
Вчитель літератури
Бесіда
Чи варто «жертвувати необхідним в надії придбати надмірне», коли такий мізерний шанс на виграш?
Бажання легкої наживи спричинило «що найменше три злодійства». Які це злодійства?
VII. Гра «Що? Де? Коли?» - бліц турнір
На столі дванадцять секторів із конвертами-завданнями. Шість із завданнями (по три завдання з кожного предмета (див. додаток до уроку 4)) та шість секторів – перехід ходу до команди суперника. Дзиґа визначає сектор. На виконання завдання дається одна хвилина. Якщо завдання виконано не правильно або не повністю, то хід переходить до суперника.
VIII. Рефлексія
Література – робота з епіграфом за питаннями:
1. Філософсько-матеріалістичні погляди Вольтера та Декарта.
2. Зв'язок між неминучим і випадковим.
3. Хороші і погані сторони гри.
Математика – моделювання та розв’язування задач-викликів:
1. Обчислити ймовірність, що тебе запитає вчитель, якщо в класі 10 учнів.
Розв’язання. m1,n10,P(A) 
0,110%.
2. Обчислити ймовірність отримання слова «рок» із карток, на яких написані літери «р», «о», «к».
Розв’язання. m1,n 3! 6,P(A) 
.
3. Обчислити ймовірність випадання семи очок при підкиданні двох кубиків одночасно.
Розв’язання. m 6,n 36,P(A)
.
IX. Домашнє завдання Література: скласти кросворд або створити колаж «Пікова дама».
Математика: скласти та розв’язати задачі на знаходження ймовірності випадкової події.
X. Підведення підсумків уроку
визначення переможців;
виставлення оцінок;
враження від уроку.
додаток 1
У 1830 р. в Москві доля звела Пушкіна з серпуховським поміщиком Огонь-Догановським В.С., досвідченим гравцем в карти. Одного разу в азарті гри поет програв майже 25 тисяч. Сплатити таку велику суму відразу він не міг і випросив розтермінування на чотири роки. Про цей випадок пліткували в московських салонах. Він мало не призвів до розриву заручин Пушкіна з Гончаровою. Виплати Огонь-Догановському ще довго обтяжували його душу. Безумовно одне – програш, що мало не став роковим у долі Олександра Сергійовича, став поштовхом до створення повісті «Пікова дама».
О. Пушкін Герман Ілюстрація до твору Сен-Жермен Голіцина
Коли повість вийшла в світ, Пушкін зробив запис у щоденнику: «Моя «Пиковая дама» в большой моде. Игроки понтируют на тройку, семёрку и туза. При дворе нашли сходство между старой графиней и кн. Наталией Петровной и, кажется, не сердятся…». Близькі друзі Пушкіна, Нащокіни, розповідали, що, за словами самого Олександра Сергійовича, головна зав’язка повісті не вимисел. Стара графиня – це Наталя Петрівна Голіцина, дійсно проживала в Парижі в тому статусі, як описав Пушкін. Там вона зустрічалась із графом Сен-Жерменом і справді змогла повернути статок, який програв її чоловік. Граф Сен-Жермен був знаменитою і колоритною постаттю в Парижі. Він вважав себе алхіміком, винахідником еліксиру безсмертя. ЇЇ внук Голіцин розповів Пушкіну, що одного разу програвшись в карти, прийшов до баби просити грошей. Грошей вона йому не дала, а відкрила таємницю «трьох карт» графа Сен-Жермена. «Спробуй», - сказала бабця. Онучок поставив карти і відігрався. Всі інші події сюжету – це вимисел.
Нащокін вказував Пушкіну на більшу зовнішню схожість графині з повісті на Наталію Кирилівну Загряжську, ніж на Голіцину. Пушкін погодився з цим і відповів, що йому простіше було зобразити Загряжську, ніж Голіцину.
додаток 2 Імовірнісні уявлення використовувалися людством дуже давно. Підтвердженням цього служать висловлювання давньогрецьких філософів:
«Ніщо не більше таке, ніж таке» або «Не більше так, ніж інакше» - ісономія (рівновіддаленість) – Демокріт
«…бо не більш істині чи хибні, але все одно» - що істинно, що хибно, неясно – Арістотель.
Демокрит Аристотель Паскаль Ферма
Як наука теорія ймовірностей почала розвиватися із середини XVII ст., цьому сприяла практика азартних ігор, а також страхування. Вважають, що основи теорії ймовірностей були закладені листуванням, яке виникло в 1654 р. між Блезом Паскалем та П'єром Ферма. У1657 р. Христіан Гюйгенс (1629—1695) опублікував свою роботу «Про розрахунки при грі в кості», яка стала першим виданням з теорії ймовірностей.
Кавалер де Мере, один із пристрасних гравців XVII ст., під час гри в кості помітив деякі закономірності і звернувся до найвизначнішого математика Франції того часу Блеза Паскаля з такими питаннями: «Коли гральний кубик підкинути 4 рази поспіль, що отримаємо в результаті? Найімовірніше, випаде шістка хоча б один раз чи шістка так жодного разу і не з'явиться? А при двадцяти чотирьох підкиданнях на що вигідніше ставити: що хоч раз випадуть зразу дві шістки чи цього взагалі не
станеться?»
Розв'язування цих і подібних задач такими математиками, як Б. Паскаль, П. Ферма, Х. Гюнгенс, Я. Бернулі, Т. Байок, С. Пуасон сприяло розробці основних понять і загальних принципів теорії ймовірностей. Крім того, зазначена наука багато чим зобов'язана працям наших співвітчизників П.Л.Чебишева, А. А. Маркова, О. Я. Хінчина, А. М. Колмогорова,
Б.В.Гнеденка.
додаток 3
Карти-запитання до сюжету
додаток 4 Літературні запитання
1. Що залишилося у Германа на згадку про Лізу, окрім листів?
2. Де зустрічалися графиня з Сен-Жерменом?
3. Коли графиня відкрила таємницю карт Герману?
Запитання із теорії ймовірностей
1. Що ймовірніше в нашому конкурсі: випадання питання чи переходу?
2. Де потрібно розмістити задачі з математики на столі, щоб урівноважити шанси?
3. Коли реальніше виграти у лото: 5 із 36 чи 6 із 36?
Біурок у 7 класі
Тема: Дедуктивний метод – як конститутивний для головних персонажів і читачів детективних оповідань Е. По і А. Конан Дойля та застосування його для дослідження геометричної інтерпретації формул скороченого множення.
Мета: навчити учнів узагальнювати прочитане, висувати гіпотези та підтверджувати їх фактами, удосконалити навички роботи з текстом та аналітичними виразами математичних формул; розвивати логічне та абстрактне мислення; виховати допитливість та практичність учнів.
Оформлення та обладнання класу: мультимедійне обладнання для демонстрації презентацій.
Справді це загадково, – зауважив Ватсон.
– Як ви думаєте, що це могло означати?
Поки що у мене немає фактів, – сказав Холмс. – Будувати ж теорію, не маючи фактів, –
велика помилка. Мимоволі починаєш
підганяти факти під теорію замість того, щоб пояснити теорію фактами.
А. Конан Дойль «Шерлок Холмс»
Хід уроку
I. Оголошення теми, мети, структури уроку. II. Вступне слово вчителя
Література
Брати Гонкури писали: «Детективна література водночас і божевільна, і математична». Творчість Е. По та А. Конон Дойля цілком підтверджує визначення Гонкурів. Хіба не зводить з розуму розслідування найзаплутаніших життєвих ситуацій та злочинів в творах класиків детективного жанру. І як тут обійтися без відомого дедуктивного методу – одного із методів математики. Легран і Холмс зачаровують читача чіткою логікою цього методу – підтвердження загального частковим.
Математика – робота з епіграфом
З чого розпочинається вивчення будь-якої теми?
(Означення об’єктів вивчення – «раціональні вирази»,
«одночлени», «многочлени») Розглядаються властивості об’єктів та їх взаємозв’язки.
(Закони, правила, формули, теореми) Застосування теорії на практиці.
(Розв’язування прикладів та задач) «Пояснюємо теорію фактами» - суть дедуктивного методу.
III. Математичний фрагмент – евристична бесіда
Для чого ми використовуємо формули скороченого множення на уроках математики? (мал. 1 – всі малюнки проектуються на мультимедійну дошку)
Виявляється, що в цих формулах зашифровані знання про геометричні тіла та співвідношення між величинами, що їх характеризують. Застосуємо
дедуктивний метод для розшифровки
вже відомих нам формул скороченого множення в геометричній
c d інтерпретації. З якими
мал. 2
поняттями з геометрії у вас
асоціюється «число», його «квадрат», «куб»? (довжина відрізка, площа квадрата, об’єм куба).
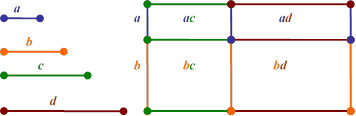
Поставимо у відповідність кожній букві формули 1, довжину відповідного відрізка (мал. 2). Як можна бачити, на малюнку зашифрована формула, що дозволяє обчислити добуток двох двочленів. Геометрична інтерпретація формули 1 дає можливість матеріалізувати теоретичні знання з алгебри.
Спробуйте самостійно (в зошитах) виконати малюнок до геометричної інтерпретації формули 2. Хто буде готовий представити свій результат, той
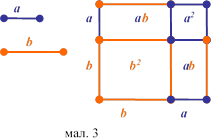
зможе отримати частинку
«скарбу Леграна» у вигляді «монети» номіналом, що відповідатиме оцінці. Вперед
за «скарбами», що зашифровані у формулах (мал. 3).
b > a
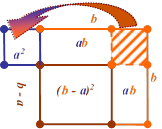
Тепер разом зобразимо a b - a a
геометричну інтерпретацію 
формули 3 (мал. 4). b
Для зображення мал. 4 b - a a геометричної інтерпретації
формули 4 прочитаємо її справа наліво, тобто знайдемо площу прямокутника зі сторонами (a + b) та (a -
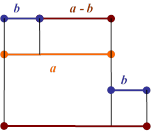b b) (мал. 5). Як видно з
малюнка 5 його площа дорівнює різниці площ квадратів із сторонами a,
a + b b, причому a > b.
мал. 5
Чи існує геометрична
інтерпретація (a - b), якщо a < b?
Чи можна матеріалізувати (зобразити) відрізок із від’ємною довжиною або квадрат із від’ємною площею, або куб із від’ємним об’ємом?
Тепер перейдемо до суми та різниці кубів (формула 6). Розглянемо геометричну інтерпретацію для різниці кубів, причому a > b (див. мал. 6).
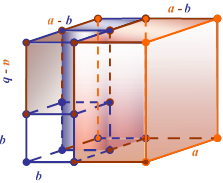V1 = a3 V2 = b3
a a3 - b3 = (a - b) • (a2 + ab + b2) =
(a - b) • a2 + (a - b) • b2 + (a - b) • ab
мал. 6
Спробуйте самостійно (в зошитах) виконати малюнок до геометричної
a3 + b3 = (a + b) • (a2 - ab + b2) = (a + b) • a2 + (a + b) • b2 - (a + b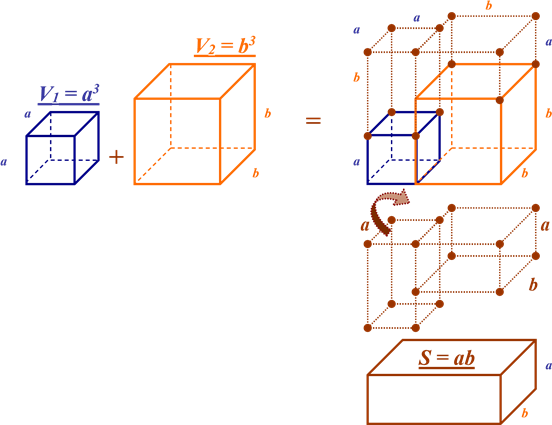) • ab
a b
S = a2 S = b2
2 b
V = (a + b) • a
V = (a + b) • b2 V = (a + b) • ab
мал. 7 a + b
інтерпретації формули 5. Хто буде готовий представити свій результат, той зможе отримати частинку «скарбу Леграна» у вигляді «монети» номіналом, що відповідатиме оцінці. Вперед за «скарбами», що зашифровані у формулах (мал. 7).
IV. Рефлексія – застосування дедуктивного методу
Задача 1. Пірат Кід на клаптику пергаменту зашифрував формулу (мал. 8).
Використаємо дедуктивний метод Холмса, щоб розшифрувати запис.
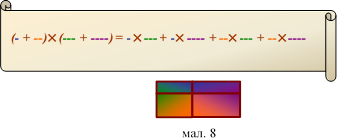Розв’язання.
Для розшифровки використаємо геометричну інтерпретацію формули 1. Отже, на папірусі зашифрована формула добутку
суми двох одночленів:
(a + b)(c + d) = ac + ad + bc +bd.
Задача 2. Лагран знайшов чотири прямокутні куски папірусу розміром 3Ï4; 4Ï5; 3Ï7; 5Ï7.
Чи є вони частинами цілого куска прямокутної форми.
Розв’язання. Застосуємо формулу з попередньої задачі для розв’язання даної.
Запишемо їх розміри у вигляді суми множників:
3 4 + 4 5 + 3 7 + 5 7 = 4 (3 + 5) + 7 (3 + 5) = (3 + 5) (4 + 7).
Оскільки сума записується у вигляді добутку, то робимо висновок, що ці куски є частинами цілого.
V. Літературний фрагмент – бесіда за питаннями:
Що таке «художня деталь» (повторення літературного поняття)?
«Мій метод ґрунтується на тому, що слід спостерігати дрібниці», - суть дедуктивного методу словами Холмса.
«Будувати ж теорію, не маючи фактів, – велика помилка» - обговорення слів епіграфа.
VI. Робота в групах з подальшою перевіркою
(для перевірки демонструється таблиця)
(вчитель літератури)
|
Записати деталі, які допомагають: |
||
|
І група – «Золотий жук» - розшифрувати таємницю скарбів Кіда |
ІІ група – «Пістрява стрічка» - розкрити таємниче вбивство |
ІІІ група – «Спілка рудих» - зрозуміти рід занять потерпілого |
|
золотий жук; човен; пергамент; малюнок жука і його обриси; нагрітий і очищений пергамент: зображення черепа, кота, шифр у вигляді знаків і цифр. |
блюдце з молоком; ліжко, міцно прикріплене до підлоги; вентиляційний отвір виведений в іншу кімнату; «псевдо» шнур для виклику; залізна шафа; батіг із петлею. |
права рука більша від лівої; шпилька для краватки із зображенням дуги і кола; вигляд правої манжети; витерте сукно на лівому лікті; татуювання у вигляді рибки; китайська монета на годинниковому ланцюжку. |
VII. Задача Леграна.
(вчитель математики)
Склавши куски, що в задачі 2 в прямокутник, Легран нагрів їх і побачив дивний напис (мал. 9). Розшифруй та отримай частинку «скарбу Леграна» у вигляді «монети» номіналом, що відповідатиме оцінці.
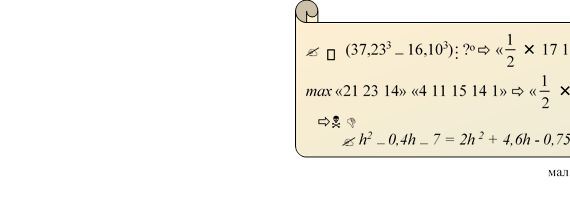
Розв’язання. Розглянемо першу стрічку (з презентацією на мультимедійній дошці):
?
(37,233 – 16,103)M?о ð «
Ï 17 11 27»2 + «21 24 11 6».
? (37,233 – 16,103)M?о – обчисливши, якому числу кратний вираз, дізнаємось кут спрямовання погляду над горизонтом. Використаємо формулу
6:
(37,233 – 16,103) = (37,23 – 16,10)(37,232 +237,2316,10 + 16,102) = = 21,13(37,232 +237,2316,10 + 16,102) M 21,1321o13.
ð «
Ï 17 11 27»2 + «21 24 11 6»
- для розшифровки складемо таблицю:
|
Знак |
Значення |
|
ð |
напрямок |
|
«…» |
рамки слова |
|
|
пів |
|
Ï |
об’єднання двох слів в одне |
|
17 |
н |
|
11 |
і |
|
27 |
ч |
|
21 |
с |
|
24 |
х |
|
6 |
д |
|
«…»2 |
повтор слова |
|
+ |
об’єднання двох слів |
Отже, читаємо:
«напрямок північ-північ-схід».
VIII. Самостійна робота в групах (по чотири учні) – мозковий штурм.
Далі учні працюють над розгадкою зашифрованого самостійно. Після чого презентують хід розслідування. Дають повний текст зашифрованого запису на папірусі:
«кут над горизонтом 21о 13/ напрямок північ-північ-схід найгрубіший стовбур сьома гілка на південь від черепа вертикально вниз на висоті 2,5».
IX. Скласти досьє – учні отримують роздруковані вклейки та заповняють їх самостійно за варіантами (див. зразок) – вчитель літератури.
зразок вклейки записи за варіантами
|
|
|
X. Гра – «відгадай науку за цитатою»
(вчитель літератури зачитує цитату з тексту, а учні за її змістом визначають науку, знання з якої застосовують Легран та Холмс)
«Золотий жук»
«…споконвіку існували …препарати для невидимих записів на папері або пергаменті – прочитати їх можна лише після нагрівання.» (Хімія)
«Простягши… рулетку від стовбура дерева до кілочка, він відміряв ще п’ятдесят футів по прямій і таким чином установив нову кінцеву точку…» (Геометрія)
«… напрямок я визначив за кишеньковим компасом, а тоді, піднісши трубу під кутом десь так у двадцять один градус, став водити нею вгору-вниз…» (Географія, геометрія)
«У цьому легко пересвідчитись, підставляючи на порожнє місце одну по одній усі літери абетки.» (Знання мови) «Спілка рудих»
« - Дайте мені роздивитися, - сказав Холмс, зупинившись на розі й уважно розглядаючи один за одним будинки. – Я хочу запам’ятати, в якому порядку розташовані будинки.» (Геометрія – просторова уява)
«… постукавши палицею по бруківці… я дізнався, в який бік робиться підкоп…» (Музичний слух) «Пістрява стрічка»
«- Болотяна гадюка! … - Найсмертоносніша індійська змія! Він помер через десять секунд після укусу.» (Зоологія)
«… вдатися до отрути, якої не можна знайти хімічним шляхом. Перевагою цієї отрути … було й те, що вона діє миттєво.» (Медицина)
«- Гм! – буркнув він, задумливо почухуючи підборіддя. – Моя первісна гіпотеза не підтверджується фактами. Коли віконниці зачинені, у ці вікна не влізти… Добре, подивимось, чи не вдається нам з’ясувати що-небудь, оглянувши кімнату зсередини.» (Будівництво, архітектура) XI. Підведення підсумків.
XII. Домашнє завдання
Підготуватися до тематичних контрольних робіт.
Біурок у 5 класі
Тема: Л. Керролл – письменник, математик-рекреаціоніст*.
Мета: навчити учнів більш глибше сприймати вивчений матеріал, вдумуватись у зміст слів та математичних формул; розвивати увагу, логічне та абстрактне мислення; виховати інтерес до пізнання.
Оформлення та обладнання класу: мультимедійне обладнання для демонстрації презентацій.
— Мистер Доджсон,— сказал любопытный малыш,— Я на лбу твоем вижу морщины.
Но так остро и весело ты говоришь! В чем же дело?
Открой мне причину.
— В ранней юности,— Доджсон ему отвечал,— Математиком был я, признаюсь,
Чтобы разум мой робким, как Кролик, не стал Или диким, как Мартовский Заяц.
— Ты мудрец, Льюис Кэрролл,- продолжил малыш,— В древнем Колледже ты обитаешь.
Но, коль разум твой ясен, как ты говоришь,— Ты, должно быть, истории знаешь?
— В ранней юности,— Кэрролл ему отвечал,— Я рассказывал много, не спорю.
И тогда-то мой ум, как ребенок, играл.
Елінор Фарджол, Англія
(Переклад О. Сєдакової)
Хід уроку
I. Оголошення теми, мети, структури уроку.
II. Словникова робота
Математика (завдання на слайді 1)
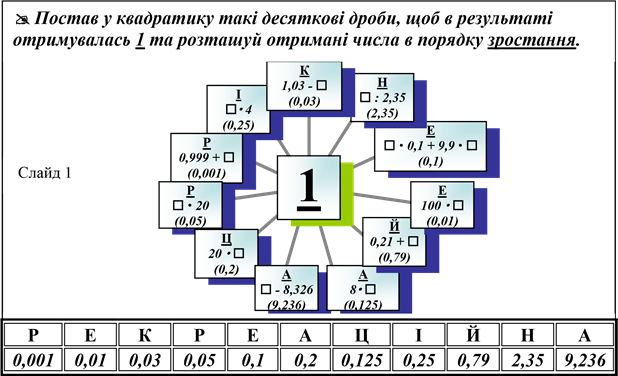
Література
* Рекреаційна математика (від англ. recreation – розваги, ігри) – математичні головоломки, ігри.
III. Гра словами
Література
«Гра в слова словами»
«My tale is long and sad», - сказала мишка.
(«Моя розповідь довга і печальна»)
«Her tail is long. It is clear, but why is it sad? », - подумала Аліса.
(«Її хвіст довгий. Це ясно, але хіба він сумний?»)
Весь текст казки – це суцільний каламбур. Так автор намагається показати багатозначність слів або словосполучень. Манера письма заставляє уважніше ставитися до слів, бо вони часто означають більше, ніж здається на перший погляд.
Робота над текстом
Знайдемо уривки з тексту, де Аліса розмірковує над значенням слова придушення або коли Герцогиня шукає у всьому мораль.
Щоб розвинути в себе змістовне ставлення до слів, зіграємо у гру Керролла «гра в слова словами». Потрібно, змінюючи ланцюжком лише одну букву в слові, отримати із вихідного слова зовсім інше. Пригадаємо, як в голові Аліси перетворюються кішка в мишку або дитина герцогині в порося (див. слайд 2).
|
кішка ð кишка ð мишка son ð sow ð saw ð say ð pay ð pat ð pit ð pig Спробуємо перетворити крик грифона на скрип грифеля: грифона ð гри фон я ð гра фон я ð гра фен я ð гри фен яð грифеля море в сушу: море ð горе ð гора ð кора ð кома ð кума ð сума ð суша. Самостійно карти в нарди: карти ð (парти ð нарти) ð нарди загнати мишу в нору: миша ð(тиша ð туша ð душа ðдума ð дама ð ð рама ð раса ð роса ð рота ð нота )ð нора злови рибу в морі: риба ð (рима ð рама ð рада ð вада ð вода ð мода ð ð мора ð тора ð нора ð гора ð горе) ð море |
||
|
|
Слайд 2 |
|
Розповідь вчителя
Гра для Керролла – звичайний стан, а розваги для нього на кшталт споживання їжі.
В своїй статті «Пожива для розуму», письменник встановлює правила харчування для розуму, приймаючи за основу правила харчування для шлунку.
«Сніданок, обід, чай. В гіршому випадку перший сніданок, другий сніданок, обід, пообідник, вечеря і стакан чогось гарячого перед сном. Яку турботу ми проявляємо про раціон для нашого щасливого тіла! Хто з нас приділяє стільки уваги своєму розуму? В чому причина такої різниці? Невже з двох – тіла і розуму – перше суттєво важливіше за друге? Ні! Я вважаю за доцільне вивести правила харчування для розуму.
По-перше, ми повинні турбуватися про те, щоб наш розум отримував їжу належного ґатунку: споживаючи наперед не придатний для цього роман, ми обов’язково отримуємо дурний настрій, небажання працювати, байдужість і т.д.
Наш розум почуватиметься жахливо.
По-друге, ми повинні ретельно слідкувати за тим, щоб наш розум отримував поживну їжу в належній кількості. Розумове переїдання або читання надмірної кількості літератури призводить до послаблення здатності засвоювати їжу і в деяких випадках втрати апетиту.
По-третє, якщо навіть їжа доброякісна, а порції помірні, то все одно не слід споживати надто різноманітну їжу за раз. Після того, як ми встановили потрібний ґатунок, кількість і різноманітність їжі для розуму, нам лишається дотримуватись належних інтервалів між послідовним споживанням їжі, і, не поспішаючи, ковтати їжу, тоді, коли ми ретельно її пережуємо (обміркуємо), щоб вона повністю засвоїлась.»
Для Керролла «людина розумна» значить «людина грайлива». Тому і всі персонажі його казок грають в різні ігри, загадують один одному загадки, шаради, розв’язують логічні задачі. Вони заманюють нас з вами в цей чудернацький світ так, як Білий Кролик заманив Алісу в нору, в подорож по карточній країні. Математика (проводиться у формі евристичної бесіди)
Застосування властивостей арифметичних дій до обчислень з десятковими дробами
Чому по карточній країні?
Бо саме карти – це древня гра з чітко визначеними правилами, які давно описані математичними формулами. Невипадково комп’ютери спочатку навчили грати у карти, а тоді вже у всі інші ігри.
В які ще ігри грає людина з комп’ютером?
|
а + b = b + a; a b = b a; c (a + b) = ac + bc; c (a - b) = ac – bc. |
Зіграймо і ми в гру із застосуванням властивостей арифметичних дій (див. слайд 3). Але спочатку перевіримо, наскільки вміло ви застосовуєте ці закони для обчислення виразів, що містять
Слайд 3 десяткові дроби.
Задача1. Аліса в результаті послідовних перетворень змінилась у зрості:
перший раз у 0,1, другий – у 100 раз, третій у 0,1. Який зріст мала Аліса після трьох перетворень, якщо її нормальний зріст – 1 м (див. слайд 4).
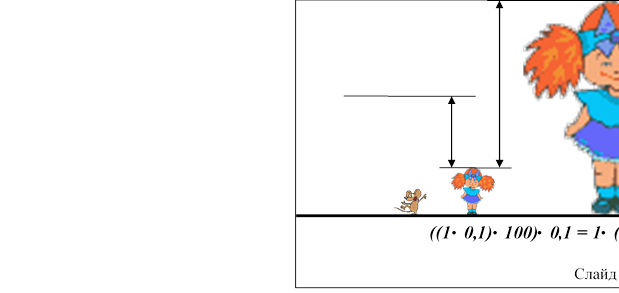
Задача 2. В перегонах по колу брали участь: птахів та звірів – по 0,543 і 0,332 від усіх учасників відповідно та Аліса з черепахою. Скільки було всіх учасників гри?
Розв’язання. Позначимо всіх учасників перегонів Х. Тоді птахів - 0,543Х, а звірів - 0,332Х. Отримуємо рівняння:
0,543Х + 0,332Х + 1 + 1 = Х; (0,543 + 0,332)Х + 2 = Х; 0,875 Х + 2 = Х; Х – 0,875 Х = 2;
0,125 Х = 2;
Х = 2 : 0,125; Х = 16.
Відповідь. 16.
Застосування властивостей арифметичних дій у грі – «створи слово»
Спробуємо перетворити сполучення слів у інші слова, застосовуючи властивість розподільного закону (див. слайд 5).
|
три (тон È нога È член) = тритон È тринога È тричлен; кіт (плюс È ГУР) = плюскіт È гуркіт = шум.
Самостійно: три (зуб È кутник) = [тризуб È трикутник = герб]; фото (граф È апарат) = [фотограф È фотоапарат = світлина]; вік (чоло È тор) = [чоловік È Віктор = козак]; блок (пост È Ада) = [блокпост È блокада = буфер] |
||
|
|
Слайд 5 |
|
IV. Перетвори вірш у каламбур (див. слайд 6)
|
|
||||||
|
|
Слайд 6 |
|
||||
V. Самостійна робота (див. слайд 7, 8)
Слайд 7 |
||||
Слайд 8 |
VI. Домашнє завдання:
література – перефразувати вірш; перетворити «слово словами».
математика – записати перетворення слів за розподільною властивістю; розгадати секрет фокуса (див. слайд 9)
|
Магія десяткових дробів Виконай послідовно: 1. Задумай трьохзначний десятковий дріб, що складається з одиниць, десятих та сотих; 2. Запиши його навпаки та від більшого відніми менший; 3. Запиши різницю навпаки та додай. Наприклад:
2,54 - 4,52 1,98 + 8,91 10,89 Слайд 9 |
Біурок у 8 класі
Тема: Філософські аспекти поетичної і математичної спадщини Омара Хайяма.
Мета: навчити учнів виявляти актуальність творів, вічність порушених у них проблем; розвивати логічне та абстрактне мислення; виховати інтерес до творчої спадщини філософа.
Оформлення та обладнання класу: мультимедійне обладнання для демонстрації презентацій.
Я тільки й знаю, що знання шукаю, В найглибші таємниці проникаю.
Я думаю вже 72 роки –
І бачу, що нічого я не знаю.
Омар Хайям
Хід уроку
I. Пролог (вчитель літератури)
В одній медресе́
навчалося троє юнаків. В стінах школи вони потоваришували і, як годиться
справжнім друзям, дали один одному клятву: той, хто першим доб’ється успіху в
житті, допоможе іншим. Ніхто з них тоді не знав, що один з друзів стане
візиром, другий очолить релігійну секту, а третій прославиться як великий
вчений і
поет. Це були Нізам аль Мулк, Хасан ас-Саббах і Омар Хайям.
Першим добився успіху Нізам. Він став візиром сельджукського султана Малик-шаха, який правив у Персії. Пам’ятаючи клятву, він допоміг друзям. Хасану він дав місце при дворі. Але з часом він поїхав в Єгипет, де став послідовником ісмаїлітів (релігійної течії в ісламі). Омара, якого не цікавили високі пости і багатство, він забезпечив належними засобами, щоб той міг безбідно жити в рідному місті, займатися науками і писати рубаї.
II.
Оголошення теми, мети, структури уроку.
III. Енциклопедична пауза (вчитель математики) Філософські концепції – ідеї і думки про людське буття.
До 1080 року належить перша праця Омара Хайяма — «Трактат про буття і повинність».
Трактат був написаний у відповідь на лист імама
та судді ан-Насаві, який пропонував «царю філософів Заходу і Сходу Абу-льФатгу ібн Ібрагіму Хайяму» висловитися в питаннях «про мудрість творця у створенні світу й особливо людини, і про необхідність людям молитися». До цього трактату належить також «Відповідь на три питання: необхідність
протиріч у світі, детермінізму (вирішального фактору) та довговічності», у передмові до якої Хайям зазначив, що він не чекав, що «йому поставлять питання, де міститься такий сумнів».
Спробуємо побачити в спадщині О. Хайяма його філософські позиції. IV. Літературна сторінка
Вчитель літератури
В літературі Омар Хайям відомий завдяки своїм рубаї. Але через труднощі перекладу, а також через велику
кількість метафор, використаних автором, не
всі його твори перекладено правильно. Деякі навіть стверджують, що Хайям
засуджував Аллаха, несправедливість життя та був п’яницею
та розбишакою, адже писав про вино і любов до жінок.
Насправді, це хибно. Просто автор використовував образи, порівняння та тонкий
підтекст. Насправді він був глибоко духовною та мудрою людиною, вірив у Бога. Про
це свідчать багато джерел, наприклад, Чарльз Хортон у передмові до «Рубайят»,
випущеного у Лондоні у 1917 році, писав:
«У Персії нема суперечок щодо віршів Омара і їх
значення: автор шанується як великий релігійний поет. Його возвеличення вина і любові представляють собою класичні суфійські метафори: під вином розуміється духовна радість, а любов – радісна вірність Богу... Омар не виставляв свої знання напоказ, а камуфлював їх. Абсурдно відноситися до подібної людини як до п’яниці та нероби, однак його глибокі вірші, які здаються на перший погляд поверхневими, вводять в оману.»
Юначе, підведись — горить зоря ясна!
В прозорі келихи налий вогню-вина!
В цім тліннім закутку живеш ти мить… а потім, Хоч як жадатимеш, не вернеться вона.
Російський поет, драматург С. Я. Маршак так відізвався про поета:
Четыре строчки источают яд,
Когда живёт в них злая эпиграмма, Но раны сердца лечит Рубайят –
Четверостишия старого Хайяма.
Авторський переклад:
Чотири стрічки випускають яд,
Коли живе в них жовчна епіграма, Та рани серця лічить Рубайят – Чотиривірші мудрого Хайяма.
Поетичний калейдоскоп – читання поезій напам’ять; групування за змістом та висвітлення філософських питань буття
Про проблеми довговічності: що життя коротке, а час швидкоплинний, що треба жити сьогоднішнім днем, радіти кожній миті.
I юних, і старих – всіх поглинає час, I невеликий нам дається днів запас.
Ніщо не вічне тут: ми підемо так само, Як ті, що вже пішли й що прийдуть після нас.
Що ти вартий на світі без волі небес?
Ти помреш – і не станеться жодних чудес. Краще жити сьогоднішнім щастям химерним, Ніж чекати біди, як зіщулений пес.
У колисці – дитина, покійник – в труні.
Ось і все, що про долю відомо мені.
Скільки віз не наповнюй пожитком-скарбами, Все одно до межі добредеш впорожні.
Хайям закликає бути людей добрими, чесними, не вихвалятися своїми багатствами та знаннями. Тобто, у будь-якій ситуації треба залишатися Людиною. Ти до зла не хились, а роби лиш добро!
Бо не зло тобі друг, а добро, лиш добро. Якщо зло і добро тобі в друзі прибились, Вибирай однозначно - добро, лиш добро!
Марнославцем, для влади придатним, не будь.
Будь бальзамом. Отруті подібним не будь. Якщо прагнеш життя не прожить як нікчема, Не збивай на дурне і злостивим не будь.
Не годиться вдаватись до лайки й образ, А люб'язність тримати лише про запас. Не розумно хвалитись нажитим багатством, Не годиться знання виставлять напоказ.
Йди з добром до людей – і воздасться тобі. Скромним будь - і не згубишся ти у юрбі.
Із маленьким муравликом краще зріднися,
Аніж з тим, хто в гордині погруз і чваньбі.
Про необхідність протиріч у світі.
Весь оцей небозвід видається мені
Мов великий ліхтар із вогнем в вишині,
Той вогонь — наше сонце, а світ — ніби сцена, Ми — немовби танцюючі тіні смішні.
Джерело ми розваги і смутку копна, В нас — Всевишній живе і живе сатана, Бо людина, як світ цей, багатоманітна, Ми — провалля і ми ж таки — височина!
Для достойних немає достойних відзнак, Я достойному дам свій останній мідяк.
Хочеш знати, чи пекло існує насправді?
Суще пекло — це жити в гурті вовкулак.
Мене всі недруги філософом зовуть.
Бог свідок, що обрав собі я іншу путь. Прийшовши з безвісті у цю долину горя, Принаймні знаю я, ким сам я хочу буть.
Про вчора не гадай — воно навік зів'яло, Про завтра не журись — воно ще не настало.
Минуле й завтрашнє — підпора ненадійна! Живи хвилинами, бо в тебе їх так мало!
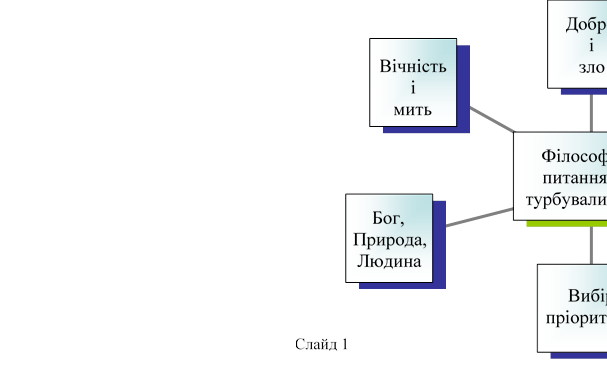
V. Філософська сторінка
Колективне складання схеми (див. слайд 1)
VI. Математична сторінка (евристична бесіда)
У Ісфахані, при дворі Малік-шаха, Омар Хайям займався математикою. Відомі математичні результати, досягнуті Хайямом, відносять до трьох напрямків: до алгебри, до теорії паралельних та до теорії відношень і вчення про число. Математичні праці О. Хайяма стали відомими математикам Європи зовсім недавно.
Теорії відношень і вчення про число – енциклопедична пауза
Ми вже маємо поняття про числа: натуральні, цілі, раціональні, ірраціональні, дійсні (див. слайд 2).
Друга та третя книги «Трактату
про тлумачення темних положень у
Евкліда» присвячені теорії відношень.
Знову базуючись на згоді з
Аристотелевою точкою зору, він так сформулював принцип неперервності: «Величини можна ділити нескінченно, тобто вони не складаються з неподільних величин». Разом з тим, він
пішов далі та ввів нове визначення пропорції, в якому рівність відношень зводилась до збігу їхнього розкладання на неперервні дроби. Він довів еквівалентність своєї теорії відношень з теорією Евкліда, пов'язав вже дві дійсні теорії (відношень чисел та загальної теорії відношень), та, базуючись
на
принципі неперервності, встановив при цьому існування загальної теореми про
існування четвертої пропорційної до трьох даних величин. У третій книзі Хайям
звернувся до множення відношень і саме тут по-новому трактував зв'язок понять
відношення і числа. Він висловився за введення в математику подільної одиниці та нового роду чисел, за допомогою яких можна було б
виразити будь-які відношення величин.
Знаходження четвертої пропорційної величини до трьох даних
|
|
3 На уроках геометрії ми навчилися будувати четвертий пропорційний відрізок з |
використанням узагальненої теореми Фалеса. Використаємо це у наступній задачі.
Задача. Знайти відношення: варіант 1 – площі квадрата до його діагоналі; варіант 2 – площі прямокутника до його діагоналі (див. слайд 3).
Ірраціональні
числа 2;_
3,1415926...;_e
2,7182818... -
нескінчені десяткові дроби.
Зобразимо
відрізок довжиною 2
(див. слайд 4).
Чи можна зобразити нескінчене число скінченою довжиною відрізка?
Це протиріччя між
геометрією і алгеброю, що прийшло від древньої Греції, успішно вирішив О. Хайям
задовго до Декарта, Ньютона та Кантора. На відміну
від Евкліда та інших давньогрецьких математиків,
Омар Хайям не тільки не протиставляв числа неперервним величинам, геометрію —
арифметиці, а й намітив
конкретні шляхи до виявлення єдності протилежностей, до ліквідації прірви між дискретністю та неперервністю.
Вчений використав філософську концепцію необхідності протиріч – невід’ємної властивості вербального мислення.
Зображення ірраціональних чисел.
Дійсні числа, як і раціональні,
можна зображати на числовій осі точками. Нехай дано числову вісь (див. слайд 5)
з початковою (нульовою) точкою О і одиничним відрізком ОА. Зобразимо
на цій осі точку, що відповідає ірраціональному числу 2 . Для цього будуємо на відрізку ОА квадрат,
його діагональ ОС = 2 .
Якщо розхилом циркуля ОС провести дугу до перетину її з віссю, то
одержана точка К і буде відповідати числу 2 .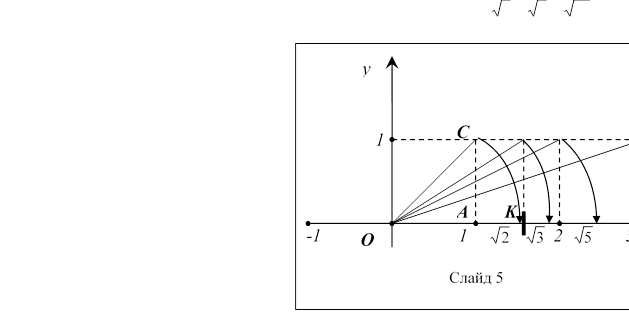 
Аналогічно отримуємо: 3;_ 5;_ 10 . точок числової
осі і множиною дійсних чисел існує взаємно однозначна відповідність.
Але між множиною точок числової осі та множиною раціональних чисел не існує взаємно однозначної відповідності, оскільки не кожній точці осі відповідає раціональне число.
Наближені значення квадратних коренів.
Ще одна математична праця Хайяма — «Труднощі в арифметиці» — була присвячена методу знаходження коренів будь-якого ступеня з цілих чисел; в основі цього методу Хайяма лежала формула, що пізніше одержала назву бінома Ньютона. Цей трактат не знайдений, але його згадував сам Хайям у «Трактаті про доведення задач алгебри та алмукабали».
Щоб добути
квадратний корінь з багатоцифрового цілого числа (279841), розбивають його
справа наліво на грані (див. слайд 6), що містять по дві цифри (в
крайній лівій грані може виявитися і одна цифра). Щоб одержати першу цифру
кореня (5), добувають квадратний корінь з найбільшого точного квадрата, що
міститься в першій зліва грані (27). Потім віднімають від першої грані квадрат
першої цифри кореня (25) і до різниці приписують (зносять) наступну грань (98).
Зліва від одержаного числа (298) пишуть подвоєну першу цифру кореня (10),
ділять на неї число всіх десятків раніше одержаного числа (29:10 2),
випробовують частку (102 2=204 повинно
бути не більшим за 298), записують його (2) після першої цифри кореня. Далі аналогічно. Підкреслюють і справа від вертикальної лінії записують різницю: 298 – 204 = 94. Зносять наступну грань – 41. Тобто – 9441. Зліва від одержаного числа записують подвоєну цифру кореня – 52 2 = 104 та цілу частину числа, що отримується від ділення числа десятків числа справа (9441) на подвоєну цифру кореня (104), тобто 9 944 : 104. Записуємо приблизну частку як третю цифру кореня – 529, дописуємо четверту цифру до числа зліва – 1049 і множимо на отримане число – 1049 9 = 9441. Підписуємо під числом справа добуток та віднімаємо. Якщо результатом різниці є 0, то добування квадратного кореня закінчено.
Аналогічно добувають квадратні корені з десяткових дробів (див.
слайд 7). При цьому
підкореневе число треба розбивати на грані так, щоб кома була між гранями
Якщо десятковий дріб має непарне число десяткових знаків, з нього точно квадратний
корінь не добувається.
Наближені значення квадратних коренів.
Якщо підкореневе число наближене, то квадратний корінь з нього також буде наближеним числом. Квадратні корені з наближених чисел можна добувати так само, як і з точних, але з урахуванням правила підрахунку цифр.
При добуванні квадратного кореня з наближених чисел в результаті зберігають стільки значущих цифр, скільки їх містить підкореневе число. Щоб правильно визначити останню значущу цифру, шукають в результаті на одну значущу цифру більше, ніж у підкореневому числі, а потім результат округлюють за правилом округлення, відкидаючи цю запасну цифру.
Однак наближені значення квадратних коренів одержують не тільки в результаті добування квадратних коренів з наближених чисел, а також і з
точних. Нехай, наприклад,
треба добути квадратний корінь з точного числа 2 (див. слайд 8).
Процес добування квадратного кореня
з числа 2 є безкінечним. Тому 2
у вигляді десяткового дробу можна подати тільки наближено з будь-
якою точністю.
VII. Самостійна робота на два варіанти
Знайти наближене значення з
точністю до тисячних для чисел: варіант 1, 2 – 3 5 відповідно.
VIII. Робота з епіграфом
Таким чином, чи не основний, філософський принцип Омара Хайяма – необхідність протиріч у світі – стає рушійним у розвитку науки, дає можливість в будь-яких протиріччях знаходити раціональне зерно, відправну точку для руху вперед, відкривати все нові й нові таємниці буття.
IX. Домашнє завдання.
Література – знайти у творчості поета відповідь на три питання:
необхідність протиріч у світі, пріоритетів та довговічності.
Математика – обчислити до тисячних: 54756 7 .
Біурок у 5 класі
Тема: Повторення та систематизація знань з тем «Казки народів світу» і «Розв’язування текстових задач».
Мета: структурувати отримані знання з предметів у систему особистісних знань учнів; розвивати уміння аналізу і синтезу, навички самостійного мислення; формувати ціннісні життєві орієнтири.
Оформлення та обладнання класу: мультимедійне обладнання для демонстрації презентацій.
Література – цариця душі.
Математика – цариця наук.
Хід уроку
I. Оголошення теми, мети уроку
II. Словникова робота – дефініція об’єктів вивчення на уроці
Вчитель математики
Учні отримують на кожну парту набір пазлів, самостійно складають прямокутник (див. слайд 1), а потім звіряють за слайдом (використати анімаційні властивості руху об’єктів – геометричних фігур у режимі PowerPoint).
«Фабула» – умова задачі; розповідь про задачу; постановка задачі. Вчитель літератури
«Фабула» (лат. fibula – байка, розповідь, переказ, історія) – елемент сюжету, що визначає межі руху сюжету в просторі й часі; розповідь про події, зображені у творі, на відміну від самих подій – сюжету твору.
У виділеному стовпчику кросворда зашифроване слово, значення якого - «шлях» (див. слайд 2).
По горизонталі: 1. Хто
примушував Хлопчиказірку шукати золоті монети?
2. Художник, картини якого оживали.
3. Постільний раджи Какудрума.
4. Наречений Елізи.
5. Морська красуня, що поселилася на дереві.
6. Купець-мандрівник. 7. Бабуся, що «виробляє» сніг. 8. Малюк, що переміг велетнів Оні. Вчитель математики
«Алгоритм» (aldoritmus – лат. транслітерація імені аль-Хорезмі) – шлях
(план) розв’язання текстових задач або будь-яких математичних задач. III. Зав’язка – аналіз слайда (див. слайд 3) – евристична бесіда
Вчитель математики
Чи
застосовували ви математичні знання, читаючи казки? Наведіть приклади.
Вчитель літератури
Навпаки – чи знадобились знання літератури при розв’язуванні текстових задач?
Наведіть приклади.
Тож читаючи казку, ми
підсвідомо використовуємо знання з математики і навпаки.
Випереджальне домашнє завдання – презентація математичних об’єктів із казок. Клас ділиться на чотири групи, кожна група презентує по дві казки (див. слайд 4).
Слайд 4 |
IV. Математична сторінка – розвиток навичок аналізу та синтезу
Вчитель математики
Літературний текст задачі –– фабула – переводиться на математичну мову – символи – символи пов’язують у вирази – вирази у формули або рівняння, які виражають кількісні співвідношення між об’єктами задачі.
|
АЛГОРИТМ – ШЛЯХ 1. Уважно прочитати текст задачі; 2. Визначити величину, яку потрібно знайти та позначити невідому буквою: x, v, s, t, S, a, b, …; 3. Встановити співвідношення між відомими та невідомими величинами, використовуючи арифметичні дії та формули; 4. Скласти рівняння, що є символічним записом фабули задачі; 5. Розв’язати рівняння – знайти невідому; 6. Визначити всі невідомі об’єкти задачі; 7. Проаналізувати отримані результати, записати відповідь.;
Слайд 5 |
Таким чином, щоб розв’язати текстову задачу необхідно дотримуватись алгоритму (див. слайд 5). Учні отримують вклейки в зошит з алгоритмом.
Випереджальне
домашнє завдання –
презентація основних типів текстових задач. Клас ділиться на групи і кожна група презентує свою текстову задачу з
використанням сюжетів казок та показує її розв’язання згідно записаного алгоритму. За результатами презентацій визначають переможців та нагороджують дипломами І, ІІ, ІІІ та IV ступенів.
Текстові задачі можна розділити на чотири класи (див слайд 6).
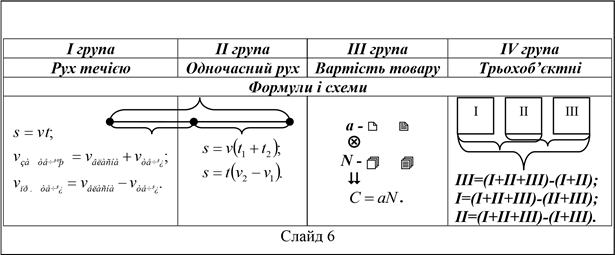Класифікація текстових задач
Текстові задачі із розв’язаннями готуються для презентацій наперед (див. слайд 7).
Слайд 7 |
V. Літературна сторінка – розвиток навичок аналізу та синтезу
Вчитель літератури – бесіда за питаннями
Чи можна сюжет казки подати у вигляді алгоритму?
Що доводиться вирішувати героям казок?
Хто перемагає в казках?
Таким чином, фабула будь-якої казки має чітку структуру – схему казки (див. слайд 8). В літературі схеми казок схожі до алгоритму в математиці. Учні отримують вклейки в зошит алгоритму та аналізують їх.
АЛГОРИТМ КАЗКИ
1. Головний герой, персонажі, що його оточують;
2. Проблеми, що постають перед героєм;
3. Дії героя у досягненні мети;
4. Чудесні помічники героя, чарівні предмети;
ô
5. Подолання труднощів (випробування, перешкоди, зло)
6. Нагорода за шляхетність – щасливий кінець.
Слайд 8
Творче завдання робота в групах – скласти і презентувати алгоритм казки (див. слайд 9). За результатами презентацій визначають переможців та нагороджують дипломами І, ІІ, ІІІ та IV ступенів.
Слайд 9 |
||||||||||||||||
Вчитель математики
Спробуємо створити математичну казку за алгоритмом. Оскільки на уроці ми використовували різні математичні формули, то й героями казок нехай будуть букви, якими записують їх або математичні об’єкти, що зустрічають в казках.
Продовжують працювати в групах. Випереджальне домашнє завдання із презентаціями казок та нагородженням дипломами (див. слайд 10). Вчителі допомагають у підготовці презентацій.
|
|
||||||
|
№ гр. |
Зміст казки |
|||||
|
І |
Якось давно, ще за часів Піфагора, жили собі в місті «Латинь» літери. Їх було лише 52. За «віком» вони були «великі» та «малі», у кожної великої була своя мала, тобто, 26 великих і 26 малих. Окрім того, кожна пара мала своє «ім’я». Вони так і кликали одне одного: S – «ес велика», s – «ес мала». Літери не мали якогось певного роду занять. Хто чим хотів, тим і займався. Жили собі не тужили, аж поки не вибрали в президенти пані «Математику». Та страшно любила скрізь порядок і точність. Тому вирішила дати кожній букві професію – чим має займатись, що означати. Та ще й розмістила місця їхньої роботи у певному порядку – у формули. Так отримали формули: шляху ( s vt ), площі ( Sab ) та інші. З тих пір жителі «Латині» стали користуватися попитом у всьому світі. Життя їхнє стало щасливим. |
|||||
|
ІІ |
|
Жив собі, був собі Гномик старенький. Мав собі білу, як сніг, бороденьку. Всі поважали за мудрість його, Рівністю звали всі гнома того. Рівність по світу невтомно блукав, Бо таємничий він корінь шукав. А як знаходив, то дуже радів. |
|
— Може, не варто той корінь шукати, Труднощів стільки в дорозі долати? Гном на березовий сперся ціпок: — Слухайте, діти, уважно урок. Дуже багато рівнянь є в житті, |
|
|
|
Потрібно для кожного корінь знайти. Ви ж починаєте з парти шкільної, З пошуків «ікс» та задачі важкої. Раджу: хай труднощі вас не лякають, Той переможе, хто їх подолає. Р. Б. Аксельрод |
||||||
|
Ніжно лунав тоді радісний спів.
Діти спитати його захотіли: |
||||||
|
ІІІ |
Одного разу горда лебідь «Шлях» Але подорожуючи річкою, героїня зіткнулася із труднощами. То вона завчасно припливала в місто, що знаходилось за течією, то вона запізнювалась, коли пливла проти течії. «В чому тут проблема?» - подумала горда лебідь. «Ми тобі допоможемо», - сказали з берега два добрих і кмітливих товариша -
З тих пір вони завжди вирушали у подорож річкою разом у човні під назвою «Формула» і в них не виникало більше проблем із вчасним прибуттям. |
|||||
|
IV |
|
|||||
|
Слайд 10 |
||||||
IV. Робота з епіграфом
V. Домашнє завдання
Створити казку з математичними елементами.
6 клас Біурок: література і математика
Тема: Урок-подорож: за романом Р. Стівенсона «Острів скарбів», множення раціональних чисел.
Мета: структурування отриманих знань з різних предметів у систему особистісних знань учнів; розвиток їхніх умінь аналізувати і систематизувати, навичок самостійності мислення; сприяння формуванню ціннісних орієнтирів у житті.
Обладнання: дидактичний матеріал, фішки - «чорний знак», підручники із зарубіжної літератури і математики, епіграфи до уроку, малюнки до твору, атрибути та одяг героїв роману ( див. додаток 1).
Знання – це найдорожчий скарб, його не зариєш.
Козьма Прутков Подорожі розвивають розум.
Честерфілд Хід уроку
I. Оголошення теми, мети, структури уроку.
II. Актуалізація опорних знань проводиться у формі бліц-конкурсу «Вибори капітанів».
Конкурсні питання (М – вчитель математики, Л – вчитель літератури):
• М. Який із добутків більший: - а. а чи - а (-а)? Поясни.
• Л. Які пригоди трапилися з Джимом до плавання?
• М. Яке із чисел менше: (- 6) 3 чи (- 1) 2 ? Поясни.
• Л. Що знаходилось в скрині Біллі Бонса і цікавило піратів?
• М. Обчисліть усно: 149,01 • 0,1 + 0,99 • 0,1.
• Л. «П'ятнадцятеро...». Продовжить піратську пісню. Хто її наспівував?
• Л. Поясніть значення слова «ватерлінія».(Ватер - вода).
• М. Яка аналогія між ватерлінією і координатною прямою, додатними
та від'ємними числами. (Нижче рівня води – < 0 та вище – > 0.)
• Л. Що викрикував Капітан Флінт, коли Джим повернувся у блокгауз?
• М. Задача 1. Скільки грамів золота було в одному піастрі, якщо він дорівнював десяти унціям, а одна унція дорівнює 1/16 фунта – одиниця маси – 453,5924 г?
Капітанами призначаються двоє учнів, які набрали найбільшу кількість балів (з більшою кількістю балів – капітан джентльменів, з меншою – капітан піратів).
III. Перевірка знань, умінь та навичок з математики і літератури, а також їх творче застосування шляхом змагання команд. (Капітани по черзі вибирають членів команди і отримують карту маршруту. На маршруті вказані зупинки – конкурси. За поразку у конкурсі команда отримує фішку – «чорний знак».
Команда, що отримає більше фішок – програє.)
Зупинка - «Порт»
Відповідно назві команди скласти «алгоритм» джентльмена та пірата. Перемагає та команда, яка точніше і повніше охарактеризує свій статус.
Зупинка - «Палуба»
Задача 2. Скільки днів тривало плавання до острова скарбів, якщо у діжці вміщалося 39 відер яблук, а кожен член команди з'їдав, в середньому, 1,5 яблука в день? Відро вміщує 30 яблук.
Зупинка - «Лото»
Складіть із даних слів вислови, прокоментуйте їх, подаруйте на згадку одному з героїв роману.
• Користі, хіба, дивно, жодної, якщо, самого себе всюди, ти, що не маєш, від подорожей, за собою, волочиш.
(Хіба дивно, що не маєш жодної користі від подорожей, якщо ти
всюди за собою волочиш самого себе. Сократ).
• Зрозуміти, навколо світу, не потрібно здійснювати, небо голубе, для того, щоб, що, подорожі.
(Для того, щоб зрозуміти, що небо голубе, не потрібно здійснювати подорожі навколо світу. Й. В. Гете).
• Кількістю, подвиги героя, лише, здоланих перешкод, вимірюються.
(Подвиги героя вимірюються лише кількістю здоланих перешкод.
С. Цвейг.)
• Існує, хто; завжди, небезпека, для тих, її боїться.
(Небезпека завжди існує для тих, хто її боїться. Дж. Б. Шоу). Зупинка - «Фарватер»
Прохід до бухти зашифрований. Щоб його відшукати потрібно знати скільки метрів .міститься в 7 футах під кілем (саме стільки складає глибина фарватеру).
1. Розв'яжіть рівняння та поставте корені так, щоб із невідомих утворилося слово FUT. Після другої цифри поставте кому. Отримане число буде значенням 1 фута в сантиметрах.
|
а) – (6U – 1,23) = 1,23 |
б) 5 . (T – 3) + 1 = 17 |
в) 1⅔ . (3/5F – 119/20) = - 0,25 |
|
U - ? |
T - ? |
F - ? |
1. Виконайте ланцюжок обчислень: пірати – верх (П); джентльмени – низ
(Д).
× 1 ≤
0 то + 2,2 м
7 футів На
скільки сантиметрів
нижче чи вище ваш результат від ватерлінії?
× 0 ≤
0 то × 10
Зупинка - «Острів» Випереджуюче домашнє завдання.
За матеріалами, які підготовили члени команд, складається загальна відповідь команди про острів, описаний в романі. Перемагає та команда, яка більше і цікавіше проінформує. Право голосу мають всі члени команди.
Повідомлення учнів
Відомий пригодницький роман Роберта Льюїса Стівенсона «Острів скарбів» від початку до кінця плід багатої фантазії. Та ось що цікаво, Його твір — суцільна вигадка, але острів, описаний Стівенсоном, справді існує. Він розташований в 35 милях на південний захід від Куби. Це острів Пінос. Він має таку назву тому, що на ньому єдиному в Карибському морі, ростуть сосни (іспанською pinoc — сосна).
Острів скарбів Стівенсона за своїми обрисами, ландшафтом, звивинами рік, рослинністю, тваринним світом як дві каплі води схожий на Пінос, різниця лише в величині, книжний острів значно менший за справжній.
Ніхто сьогодні не береться стверджувати, як це сталося. Чи це випадковість, чи письменник знав про існування Піносу. Цей острів через свою погану репутацію широковідомий в Америці та Європі. Його описували в книжках, зображали на картах. Не виключено, що Стівенсон зустрічав ці описи в записках відомого англійського «королівського» пірата Френсіса Дрейка.
Історія острова багата на бурхливі події. Його відкрив 13 червня 1494 року Христофор Колумб під час своєї другої експедиції, метою якої було знайти найкоротший шлях до Індії. Колумб назвав острів Сан-ХуанЄванхеліста— на честь улюбленого учня Ісуса Христа — євангеліста Іоанна. З тих далеких часів острів змінив близько двадцяти назв, поки не став Піносом. У наш час його називають Хувентуд (острів Молоді).
У 1557 році на Піносі з'явились морські розбійники — пірати:
англійські, французькі, голландські. Саме вони і обживали цей острів, поступово перетворюючи його на піратський центр. На Піносі за різного часу знаходили укриття відомі піратські вожаки: Вільям Дампір, Джон Хокінс, Френсіс Дрейк, Генрі Морган, Франсуа Олоне, Франсуа Леклер, Бартоломе Португалець та багато інших. Там відпочивали після розбоїв, ремонтували кораблі, зализували рани, ділили здобич, робили запаси води, продуктів харчування.
Звичайно, пірати не просто так облюбували цей острів. Він мав дуже вигідне географічне положення. Минувши Атлантичний океан, флот, який прямував до Америки за наступною здобиччю, рухався біля південних берегів островів Еспаньйола (Гаіті) і Куба до Гавани. Тут він розділявся на дві частини. Одна вирушала до Мексики, інша — до Панами. Справа втому що всі коштовності, які вдавалося награбувати іспанським завойовникам, звозились по суті у два міста: Велакрус (Мексика) і Портобело (Панама). Потім награбоване завантажували на кораблі й поверталися до Гавани, з якої об'єднаний флот відпливав до Європи. Дивлячись на карту не важко зробити висновок, що з Піносу найкоротшим шляхом можна вийти на перехват флотилії як із Портобело, так із Велакруса. Друга причина, через яку пірати перетворили цей острів на базу, — його ландшафт. Тут чимало великих і малих непомітних з моря бухт, вони забезпечували влаштування засад або переховування від ворога, противників. На ньому чимало важкодоступних печер, в яких пірати ховалися до кращих часів. Пінос багатий на прісну воду, ліси.
На Піносі, звичайно, закопували скарби. Чи є вони там тепер? Місцеві мешканці не вірять в існування скарбів. Заданими істориків на морському дні біля Піносу поховано близько двох десятків кораблів. І на кожному з них могло бути золото! Тож мисливці за коштовностями і досі дошкуляють острів'янам.
Справжніми скарбами Піносу аборигени вважають запаси мармуру, величезні плантації грейпфрутів. Тепер, коли ви купите кубинський грейпфрут обов'язково згадайте острів Пінос — столицю піратства.
У Карибському морі багато островів, на яких було знайдено скарби. Острів Мона став відомий завдяки піратському вожаку Вільяму Дженнігсу, котрий заховав там золоті монети, коштовності. В 1939 році його скарби, знайдені американцями, були оцінені в один мільйон доларів. Зупинка - «Скарбничка»
• М. Задача 3. Скільки піастрів отримав кожен, хто повернувся додому, якщо 1 фунт = 9,5 піастрам? Яка маса всього скарбу? Потрібно використати результати задачі 1 та знання тексту.
• Л. Які життєві уроки здобув Джим за час подорожі?
IV. Підсумок уроку.
• Робота з епіграфами (поєднати актуальність знань з обох предметів).
• Оголошення результатів.
V. Домашнє завдання.
Додаток 1 Маршрут
1. Зупинка - «Порт»
Відповідно назві команди скласти алгоритм джентльмена та пірата. Перемагає та команда, яка точніше і повніше охарактеризує свій статус.
2. Зупинка - «Палуба»
Задача 2. Скільки днів тривало плавання до острова скарбів, якщо у діжці вміщалося 39відер яблук, а кожен член команди з'їдав, в середньому, 1,5 яблука в день?
Відро вміщує 30 яблук.
3. Зупинка - «Лото»
Складіть із даних слів вислови, прокоментуйте їх, подаруйте на згадку одному з героїв роману.
• Кількістю, подвиги героя, лише, здоланих перешкод, вимірюються.
• Існує, хто; завжди, небезпека, для тих, її боїться.
4. Зупинка - «Фарватер»
Прохід до бухти зашифрований. Щоб його відшукати потрібно знати скільки метрів міститься в 7 футах під кілем (саме стільки складає глибина фарватера).
1. Розв'яжіть рівняння та поставте корені так, щоб із невідомих утворилося слово FUT. Після другої цифри поставте кому. Отримане число буде значення 1 фута в сантиметрах.
2. Виконайте ланцюжок обчислень: пірати – верх; джентльмени – низ.
× 1 ≤
0 то + 2,2 м
7 футів На
скільки сантиметрів ваш
результат нижче чи вище від ватерлінії?
× 0 ≤
0 то × 10
5. Зупинка - «Острів»
Випереджуюче домашнє завдання.
За матеріалами, які підготовили члени команд, складається загальна відповідь команди про острів, описаний в романі. Перемагає та команда, яка більше і цікавіше проінформує. Право голосу мають всі члени команди.
6. Зупинка - «Скарбничка»
• М. Задача 3. Скільки піастрів отримав кожен, хто повернувся додому, якщо
1 фунт = 9,5 піастрам? Яка маса всього скарбу? Потрібно використати результати задачі та знання тексту.
• Л. Які життєві уроки здобув Джим за час подорожі?
Таблиця
1 піастр – 10 унцій
1 унція – 1/16 фунта
1 фунт – 453,5924 г 1 фут – 12 дюймів – 0,3048 м
1. ватерлінія – лінія води
«ватер» – вода
2. фарватер – вода глибока (вода для плавання)
3. фут – ступня
4. кіль – дно
Карта подорожі
Малюнки до етапів подорожі
-
Я мало що розумію в математиці, але як літератор - у захваті! Рекомендую до використання!
про публікацію авторської розробки
Додати розробку