Брошура "Зустріч з параметрами"

  Загальноосвітня школа І- ІІІ ступенів № 6

м. Комсомольськ, Полтавська обл..

 

 

Зустріч з параметрами

Проектна  діяльність у школі 

 

 

 

 

 

 

 

м. Комсомольськ

2012

 

 

 

 

 

 

Укладачі: вчителі математики ЗОШІ-ІІІступенів №6 Пазиненко С.В. учитель  вищої категорії, звання “Старший учитель”, Єрмачкова В.О. учитель  вищої категорії, звання “Старший учитель”.

 

 

 

 

 

 

Зустріч  з параметрами.  Навчальний проект призначений для вчителів математики та учнів 9 (10-11) класу для занять факультативу,підготовки до олімпіад, ДПА, ЗНО, для самостійної роботи учнів.

В посібник включено   задачі з параметрами,  які розглядаються  за програмою   математики базової школи. До всіх задач наведені розв’язки.

 

Рецензент  заступник з навчально-виховної роботи  Самарець О.С.

 

 

 

 

 

 

 

 

 

 

 

 

 

             

 

 Люди, не знайомі з алгеброю, не можуть уявити собі тих дивних речей, яких можна досягти за до­помогою названої науки.

                                                                                                                Г. Лейбніц

                                   ВСТУП

 

         Колектив авторів учителів математики Комсомольської ЗОШ І-ІІІ ступенів №6, пропонує навчальний проект “Зустріч з параметрами”.

       Математика в навчальному закладі повинна бути живою, а її вивчення повинно спонукати учнів до дослідницької та пошукової роботи. Спільна робота групи учнів разом із учителем дає можливість розв’язувати складні проблеми. Дослідницький, пошуковий характер мають задачі з параметром у шкільному курсі математики, а, оскільки вони зустрічаються починаючи з 7-го класу до закінчення середньої школи,ми розробили колективний навчальний проект, показавши розвя’зування задач з параметрами на різних етапах навчання (7, 9, 10 класи).

        Ми вибрали саме цю тему, щоб допомогти учням  зрозуміти те, що задарма у житті нічого не дається, скрізь необхідно докласти зусиль для досягнення своєї мети. Проектна діяльність дає можливість залучити більшу кількість учнів до роботи, поставивши перед ними визначення шляхів оволодіння новими вміннями  і знаннями, дати можливість кожному відчути радість досягнення і підбадьорювати учнів, поєднувати у відношеннях з учнями повагу, любов і вимогливість; піклуватися про те, щоб навчально-виховний процес містив у собі ситуацію успіху. Адже  сподівання на успіх живе в кожній людині, але не кожне сподівання справджується, тому що успіх неможливий без докладання певних зусиль для його досягнення.

           Наше заповітне бажання як учителів-передати школярам ту життєву мудрість, яка називається умінням жити.

 

 

 

 

 

 

Тема: Зустріч з параметрами.

 

Автори навчального проекту:

 

С.В.Пазиненко, учитель  вищої категорії, звання “Старший учитель”;

В.О.Єрмачкова, учитель  вищої категорії, звання “Старший учитель” математики Комсомольської ЗОШ І-ІІІ ступенів №6 Полтавської області.

 

Навчальний предмет: математика.

 

Назва проекту: задачі з параметрами на заняттях факультативу.

 

Тип проекту: навчальний.

 

Ключове питання:

 

“Чи завжди ми помічаємо, що невідоме число має в задачі подвійну природу?”

 

Методи:

 

1. Пошуковий.
2. Дослідницький.
3. Системний аналіз.

Тематичні питання:

 

     1. Готуємось до зустрічі з параметрами (знайомство з параметрами).

    2.  Лінійні рівняння з параметром.

   3.  Квадратні рівняння з параметром.

   4.  Графічне розв’язування рівнянь з параметрами.                

                                                                                                    

 

 

Мета проекту:

 

Домогтися засвоєння учнями поняття “параметр”  в різних видах задач; сформувати навички розв’язування  задач з параметрами на різних етапах вивчення математики; розвивати творчу активність учнів, створювати умови для вияву ініціативи учнів під час вибору завдань;розвивати інтерес, творчі здібності та інтуїцію учнів, вміння застосовувати набуті знання в нових ситуаціях, виховувати зібраність, працьовитість, охайність, організованість, графічну та математичну культуру виховувати  в учнів прагнення до самовдосконалення, задоволення пізнавальних потреб, залучення учнів  до позаурочної роботи.                                      

 

Обладнання: плакати  із схемами, прикладами розв’язаних задач.

 

Змістові питання:

 

1. Знання методів дослідження лінійних та квадратних рівнянь.
2. Уміння виділяти в задачах сталі та змінні величини та наводити у відповіді сімейство розв’язків відносно невідомої величини для всіх можливих значень сталих величин (параметрів).
3. Навички роботи з навчальною, довідковою літературою; досвід роботи з комп’ютером.

Актуальність:

 

1. Підготовка до державної підсумкової атестації  як за курс основної ,так і за курс старшої школи  а також зовнішнього незалежного оцінювання .
2. Залучення учнів до дослідницької діяльності при вивченні математики.
3. Розвиток навичок самостійної роботи з навчальною та довідковою літературою.
4. Формування навичок нестандартного підходу до розв’язання проблемних завдань.

 

Стислий опис.

 

Учні, що відвідують заняття факультативу з математики,готуючись до проекту об’єднуються в три групи, кожна з яких презентує розв’язування своїх задач з параметрами: група учнів 7 класу-лінійні рівняння  з параметрами; група учнів 9 класу-квадратні рівняння з параметрами; група учнів 10  класу-графічне розв’язування рівнянь  з параметрами.

До кінця проекту всі учні мають усвідомити й оволодіти знаннями про задачі з параметром. Уміннями їх розв’язувати, тобто знаходити сімейство розв’язків в залежності від значень параметру. Тому кожному учневі потрібно бути уважним при відповідях і повідомленнях товаришів.

 

Навчальні предмети з якими пов’язаний проект: креслення, українська мова та література.

 

Класи, яких стосується навчальний проект: 7, 9, 10.

 

Термін, необхідний для реалізації навчального проекту: до завершення навчання в середній школі.

 

Державні освітні стандарти та навчальні програми:

 

1. Освітня галузь “Математика”
   • Уміння розв’язувати лінійні, квадратні рівняння аналітичним та графічним способом.
   • Уміння знаходити кількість коренів рівняння в залежності від значення параметра.
   • Уміння будувати графіки функцій, що містять модуль та графіки рівняння з двома змінними.
   • Застосування набутих знань при розв’язуванні задач з параметрами.

 

 

 

2. Освітня галузь “Технологія”

• Знання про проектний пошук як основу творчого процесу.
• Уміння здійснювати проектну діяльність за даними умовами.
• Давати творчу оцінку досконалості результатів проектної діяльності.

3. Освітня галузь “Українська мова та література”

Формування комунікативності та літературної компетенції, що базується на знаннях, уміннях пізнавального і творчого типу, соціальних навичках, світоглядних переконаннях.

 

Навчальні цілі та очікувані результати навчання:

• Поглибити знання про задачі з параметрами, про дослідження лінійних та квадратних рівнянь.
• Практичне використання знань про рівняння при розв’язуванні задач з параметрами.
• Залучити учнів до використання дослідницьких методів під час вивчення курсу математики.

 

Учні під час проекту виробляють навички:

• Планування своєї навчальної діяльності, співпраці з однокласниками.
• Обговорення результатів науково-дослідницької діяльності та діяльності товаришів.

                    Планування реалізації проекту  

.

№ п/п	Що потрібно зробити перед початком проекту?	Хто це зробить або допоможе зробити?	Коли це слід зробити?
	Придбати/позичити необхідні пристрої, (камера, сканер, проектор, тощо)	Вчитель	Перед початком проекту
	Зарезервувати час в комп’ютерній лабораторії або бібліотеці	Лаборант	Перед початком проекту
	Знайти та зібрати книги/диски DVD/компакт-диски, що будуть використовуватись у вашому Проекті	Вчитель	На протязі двох тижнів
	Встановити до папки Вибране закладки на сайти, які будуть використовуватися в проекті	Лаборант	На протязі місяця
	Налагодити зв’язок з класом-партнером  (чи декількома класами) та обговорити умови та взаємодію для виконання спільного проекту
	Написати грант
	Провести додаткове заняття з класом	Вчитель	За тиждень до проекту
	Отримати допомогу від інших організацій (батьківської ради, місцевої спільноти, місцевої та шкільної ради)	Батьки	Потягом місяця
	Призначити спеціальний урочистий вечір для  демонстрації закінчених учнівських робіт	Вчитель	По закінченні проекту
	Розмістити статтю у шкільній газеті	Учнівський комітет	По закінченні проекту
	Розіслати інформаційний бюлетень чи статтю, в якій розміщено інформацію про майбутній проект, батькам з проханням про допомогу	Учні	Перед початком проекту
	Запросити фахівців з даної теми для зустрічі з учасниками проекту
	Запросити директора школи, представників місцевої газети для ознайомлення з роботою учнів	Вчитель	Перед демонстрацією учнівських робіт
	Придбати/отримати матеріали та приладдя для практичної роботи	Вчитель	Перед початком проекту
	Запросити батьків для допомоги	Учні	Перед початком проекту
	Розподілити час роботи на комп’ютерах/визначити час роботи по змінах	Лаборант	Перед початком проекту
	Розмістити на веб-сервері в Інтернеті учительський веб-сайт для використання учнями протягом виконання проекту	Вчитель	Перед   початком проекту
	Перевірити URL-адреси, які будуть використовувати учні. Оновити папку Вибране та свій учительський веб-сайт	Вчитель	Протягом місяця
	Визначити порядок зберігання учнівських файлів на шкільному комп’ютері та  можливості доступу до них учнями	Лаборант	Протягом місяця
	Переконатися, що учні попередньо мають відповідні навички роботи з комп’ютером, та забезпечити можливості навчання тих, хто таких навичок не має	Вчитель	Протягом місяця
	Інше:
	Інше:
	Інше:
	Що потрібно зробити протягом проекту?	Хто це зробить або допоможе зробити?	Коли це слід зробити?
	Ознайомити учнів з критеріями оцінювання їх роботи в проекті	Вчитель	Перед початком проекту
	Проглянути разом з учнями відібраний для проекту матеріал, надати рекомендації для подальшої роботи	Вчитель	За два тижні до початку
	Організувати самостійну роботу учнів в проекті	Вчитель	Перед початком проекту
	Обговорити з учнями майбутню форму подання результатів проекту	Вчитель	Перед початком проекту
	Запросити фахівців, батьків за кілька днів до того, як вони мають прийти до школи	Вчитель	За тиждень до початку
	Зробити фотографії учнів за роботою	Вчитель	Протягом місяця
	Запросити директора школи, представників місцевої газети подивитися, як працюють учні	Вчитель	Перед початком проекту
	Призначити учнівські конференції, присвячені проекту	Вчитель	За тиждень до початку
	Оцінити учнівські проекти	Вчитель	Після демонстрації робіт
	Провести оцінювання проекту в цілому, отримати відгуки про те, наскільки вдалим він був (ваші власні висновки, висновки учнів, батьків).	Вчитель	Після закінчення проекту
	Інше:
	Інше:
	Що потрібно зробити по завершенні проекту?	Хто це зробить або допоможе зробити?	Коли це слід зробити?
	Розіслати листи подяки фахівцям, батькам/особам, що допомогли у реалізації проекту своєю роботою та фінансуванням	Учнівський комітет, вчитель	Після закінчення проекту
	Очистити, видалити вміст папки Вибране та видалити допоміжні файли на комп’ютері (комп’ютерах)	Лаборант	Після закінчення проекту
	Повернути обладнання, книги, приладдя	Учні	Після закінчення проекту
	Призначити презентацію для шкільної ради, батьківської ради, місцевої ради або спонсорів	Вчитель	Після закінчення проекту
	Включити результати цього проекту в наступні уроки свого навчального предмету, для яких ці Ключове та Тематичні питання є також важливими	Вчитель	Після закінчення проекту
	Вручити нагороди та відзнаки учням	Вчитель	Після закінчення проекту
	Подумати про наступний проект, в якому можна ефективно застосувати комп’ютерні технології	Вчитель	Після закінчення проекту

 

 

                            Листок оцінювання

 

Отримав	Максимум	Математика
	10	Математична термінологія при поясненні.
	10	Є пояснення до розв’язання, малюнків, схем.
	10	Ключове запитання, показане на рівні знань учнів.
	30	Усього з математики.
Отримав	Максимум	Зміст
	5	Головна тема роботи, пов’язана з ключовими питаннями.
	5	Матеріал подано у схемах, графіках.
	5	Повідомлення виконані з використанням питань: що?, як?.
	5	Список учасників роботи, хто яку роботу виконував?
	20	Усього за зміст.
Отримав	Максимум	Оформлення
	5	Усі публікації пов’язані з ключовим питанням.
	5	Графіки, схеми, плакати використані ефективно, у належному форматі.
	5	Тексти не мають граматичних та орфографічних помилок.
	5	Зображення  (графіки, плакати, схеми) збагачують презентацію.
	20	Усього за оформлення.

 

Діяльність учнів та етапи проведення проекту.

 

На І етапі відбувається презентація теми майбутнього проекту, обговорюються основні аспекти її реалізаціі, а саме:

• формують три групи за віком і інтересами 7-А класу, 9-А класу, 10 класу;
• обумовлюються теми робіт кожної групи, джерела                  інформації, об’єми робіт.

Кожна група отримує своє завдання.

• Учні 7-А класу (4-5 чоловік) готують повідомлення про лінійні рівняння, схему їх досліджень, пропонують задачі з параметрами, при розв’язанні лінійних рівнянь.
• Учні 9-А класу(4-5 чоловік) готують повідомлення про дослідження розв’язків квадратних рівнянь,пропонують для розгляду розв’язання квадратних рівнянь з параметрами.
• Учні 10класу  пропонують для презентації задачі з параметрами, що пропонуються на ДПА і ЗНО і розв’язуються графічно.

Учні знаходять історичні відомості, розподіляють роботу між членами групи.

На ІІ етапі учні працюють в групах над джерелами інформації для розкриття своєї теми, роблять повідомлення на заняттях факультативу, обговорюють проблемні питання. На цьому етапі вчителі проводять консультації з учнями щодо доцільності інформації.

На ІІІ етапі проводиться оформлення матеріалів, узагальнення одержаних фактів у вигляді схем, плакатів, графіків. У групах обговорюються результати роботи кожного члена групи, на заняттях факультативу проводиться презентація дослідницької роботи кожної групи.

На засіданні клубу “Тріада” презентуються результати роботи над проектом. Кожна група презентує свою роботу; показує, які знання вони одержали під час роботи над проектом.

 

Підсумок роботи.

Задачі з параметрами традиційно входять до завдань державної підсумкової атестації як за курс основної, так і за курс старшої школи, а також до завдань зовнішнього незалежного оцінювання і їх мета-перевірка логічного мислення учнів. Навчальний проект “Зустріч з параметром” показав як, навчаючись у школі, учні поступово адаптуються до задач з параметрами, починаючи їх розв’язувати з 7-го класу. Розв’язування задач з параметрами під час роботи над проектом дало можливість учням повторити та узагальнити теоретичний матеріал про розв’язання рівнянь. Побудову графіків елементарних функцій та графіків рівнянь з двома змінними, сприяло формуванню у них мислення розгалуження, тобто уміння розглядати всі можливі випадки розв’язків задач в залежності від значення параметра.

 

А тепер ми хочемо дізнатись вашу думку про проект.

• Як змінились ваші знання про задачі з параметрами?
• Розвитку яких рис характеру сприяв проект (самостійності, відповідальності, працелюбності)?
• Які пізнавальні процеси були задіяні під час проекту найбільше (мислення, пам’ять, уява, увага)?
• Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевненими в собі)?
• Чи отримали ви задоволення від власної праці?

 

 Приклади учнівських презентацій.

Повідомлення учнів 7 класу:

 Приклади з параметрами е одним з найпотужніших засобів узагальнення і систематизації знань учнів, формування в них гнучкості, критичного мислення, математичних здібностей. Дійсно будь-яке рівняння (нерівність, система рівнянь або нерівностей, мішана система), що містить один чи кілька параметрів, разом з вимогою, яка подається у формулюванні завдання, утворює задачу для організації математичної діяльності. Саме тому для класу таких завдань розповсюдився термін “задачі з параметрами”. Якою б не була вимога до задачі з параметром - розв’язати рівняння (нерівність, систему), з’ясувати певні особливості розв’язків або їх кількість залежно від значень параметра, така задача безумовно  дослідницькою і вимагає від того, хто береться за її розв’язання, і високого рівня знань фактичного матеріалу, і розуміння багатьох математичних тонкощів, і особливих якостей мислення, тому розв’язування задач з параметрами є одним із визначних засобів розвитку інтелектуальних здібностей учнів.

До задач з параметрами, що розв’язуються в шкільному курсі математики, можна віднести знаходження розв’язків лінійних, квадратних, тригонометричних, логарифмічних і показникових рівнянь з двома змінними в залежності від значень параметра. Задачі з параметрами вимагають дослідницького підходу до розв’язання завдяки тому, що параметр має двоїстий характер – одночасно є і відомим, і невідомим числом.

Рівняння – це рівність, яка містить невідомі числа, позначені буквами.

Невідомі числа в рівнянні називають змінними. Змінні найчастіше позначують буквами x, y, z, хоч їх можна позначити і іншими буквами.

Приклди рівнянь:

x+5=0; 2y-3=7y; x²=9; y²(x-y)=0.

Кожне рівняння має ліву і праву частини. Наприклад:

5x-27=3x+15.

5x-27- ліва частина; 3x+15- права частина.

Число, яке задовольняє рівняння, називається його коренем або розв’язком.

Розв’язати рівняння означає знайти його корені або довести, що їх немає.

           Рівняння виду ax=bде, а, b- деякі числа, називається лінійним рівнянням із змінною х. числа а і b- коефіцієнти рівняння, а- коефіцієнт при змінній х, b- вільний член рівняння.

Розв’язуючи рівняння ми можемо мати один із випадків:

Презентація І групи 7-А клас:

• Розв’язування рівнянь з параметрами визначається залежно від допустимих значень параметрів.
• Розв’язати рівняння з параметрами означає знайти всі його розв’язки для кожної системи допустимих значень параметрів.
• При розв’язуванні рівнянь з параметрами область зміни параметрів може бути заданою Якщо не вказані межі зміни параметрів, то вважається, що параметри набувають усіх своїх допустимих значень.

 

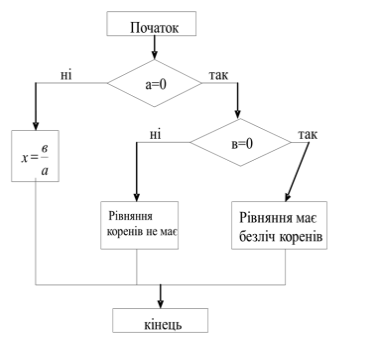
Розглянемо приклади розв’язування  лінійних рівнянь з параметрами.

Приклад 1. Розв’язати рівняння ах -3 = b залежно від параметрів а і b.

                                          Розв’язання.

 

Виконавши у рівняння ах-3 = b тотожні перетворення, дістанемо: ах = b+3.

якщо а≠0, то х = b+3/a при будь – якому b;

якщо а =0, то при b= -3 рівняння набуває вигляду 0х=0, тобто коренями рівняння є всі числа;

якщо а=0 і b≠-3, дістанемо 0х = b +3 ≠0, така рівність неможлива, тому рівняння коренів не має.

Відповідь. при а ≠0 і будь – якому b х = b+3/a ; при а =0 і b = -3 корені рівняння – всі числа; при а=0 і b≠0 коренів немає.

Приклад 2. Розв’яжемо рівняння: 1)  ах=1;  2) х-3=а+1  3).

Розв’язання

 На перший погляд відповідь очевидна: х=1/а  . Однак при а=0 дане рівняння немає розв’язків.

Відповідь. Якщо а=0, то розв’язків немає; якщо а≠0, то х=1/а

 Перетворимо спочатку рівняння х=а+4. Рівняння має єдиний розв’язок незалежно від значення параметра а. Наприклад,

якщо а=1,то х=5;  а=0,то х=4;  а=-4,то х=0.

Зауважимо,що параметр а може набувати будь-яких значень, а значення х знаходимо за формулою х=а+4.

Відповідь. х=а+4 для будь-якого значення параметра а.

Повідомлення учнів 9 класу:

               Найбільші труднощі в учнів викликають задачі з параметрами. Ці задачі найбільше відображають рівень математичного  мислення, формують початкові навички дослідницької діяльності та математичної культури. Най більший клас задач із параметрами становлять такі, що містять аналіз та дослідження квадратного тричлена з коефіцієнтами, залажними від параметра.

Класифікація задач на дослідження квадратного тричлена.

Нехай y=A(а)x²+B(а)x+C(а) - квадратний тричлен, коефіцієнти якого залежать від параметра а; D=B²-4AC – дискримінант цього рівняння; х_0=-В/2А - абсциса вершини параболи; y_0=-D/4А - ордината вершини параболи; y(α)=f(α)=Aα²+Bα+C-  значення квадратного тричлена при х= α.

Сформулюємо такі основні задачі:

1. Розв’язати рівняння A(а) x²+B(а)x+C(а)=0      (А1).
2. Розв’язати одну з нерівностей  або їх систему.

 

3. Знайти всі значення а, за яких рівняння має дійсні корені, і визначити їх знаки
4. Дослідити розташування дійсних коренів рівняння (А1) відносно заданої точки чи проміжку
5. Знайти всі значення параметра а,за яких з однієї нерівності випливає інша
6. Визначити всі значення а, за яких корені рівняння (А1) задовольняють задану умову
7. Знайти всі значення параметра а, за яких рівняння А_1 (а) x²+В_1 (а)x+С_1 (а)=0  та А_2 (а) x²+В_2 (а)x+С_2 (а)=0 мають спільні корені (або хоча б один спільний корінь)
8. Знайти всі значення а, за яких квадратний тричлен y=A(а)x²+B(а)x+C(а) чи задана функція Р(х₁:х₂), де х₁,х₂- дійсні корені рівняння (А1),  набуває найбільшого (найменшого) значення на заданому проміжку.

 Розв’язування квадратного рівняння з коефіцієнтами, залежними від параметра:

A(а) x²+B(а)x+C(а)=0   (1)

Під час розвязання (1)  треба врахувати,що при

А=0 це рівняння буде лінійним,тому рівняння (1)

еквівалентне сукупності двох систем:

   та   (2)

Якщо х₁,х₂- корені рівняння A(а) x²+B(а)x+C(а)=0, то при А>0 маємо х₁<х₂, а при А<0  х₁>х₂

.

Приклад 1. Розв’язати рівняння

 (а-2) х²-4(а+3)х+а-1=0

Розв’язання

Дане рівняння еквівалентне сукупності двох систем (див. (2)):

      та   

Розв’язуючи нерівність , знаходимо ті значення а, за яких набувають дійсних значень:

\, то

Відповідь. Якщо а=2, то х=; якщо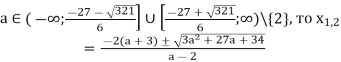

 

Приклад2.  При яких значеннях а один з коренів рівняння

дорівнює квадрату іншого?

Розв’язання. Для визначення шуканих значень а складемо систему, в якій два перші рівняння описують теорему Вієта для даного

квадратного рівняння , , а третє співвідношення містить умову, яка накладається на його корені:.

У даному випадку для визначення та зручно вибрати друге і третє рівняння системи:

  тобто

Підставляючи знайдені вирази в перше рівняння системи, одержимо:

,  ,

Відповідь. а= -1, або а=3.

 

Приклад3. При яких значеннях параметра а корені рівняння

   (1.1)

більші 1?                                                

Розв’язання

Очевидно, що задача рівносильна наступній: при яких значеннях параметра а корені квадратного тричлена   більші 1.

 

 

При а=0 рівняння (1.1) має корінь х= -1,  який не задовольняє умову задачі.

Розглянемо випадок . При таких а умови (1.3) запишуться у вигляді 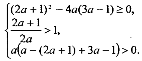   .    Розв’язуючи цю систему, знаходимо, що  . Очевидно, що цей же результат ми отримали б і розв’язуючи  нерівність  , де - менший корінь рівняння (1.1).

Відповідь. .

 

Приклад 4. При яких значеннях параметра а один із коренів рівняння

більший числа а, а другий менший числа а?

Розв’язання

Задача рівносильна наступній: при яких значеннях параметра а корені квадратного тричлена лежать на дійсній осі по різні сторони від точки ?

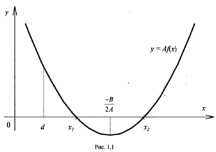
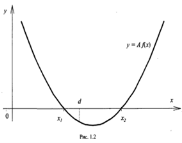
Для розв’язування цієї задачі скористаємося тим загальним фактом, що для того щоб корені квадратного тричлена (1.2) лежали на дійсній осі по різні сторони від числа d, необхідно і достатньо виконання умови (див. рис. 1.2)

Перехід від одного формулювання задачі до іншого, підкреслює загальну ідею, що пов’язана з описом тих чи інших властивостей квадратного тричлена в їх геометричній інтерпретації на графіку.

Для того, щоб корені квадратного тричлена

       (1.2)

             були більші числа d, необхідно і достатньо виконання умов

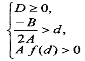      (1.3)  (див. рис. 1.1)

 

 

В нашому випадку ця умова приймає вигляд .

Тобто, вимогу задачі задовольняють розв’язки нерівності

, де

(не задовольняють вимогу задачі).

Розв’язуючи отриману нерівність, знаходимо, що

Варто сказати, що розв’язуючи цю задачу іншим способом, розглядаючи нерівності   і  досить складно.

Відповідь.

Приклад 5. При яких значеннях параметра а число корінь рівняння

² - х = 0 дорівнює а?

Рішення: побудуємо ескіз графіка функції, в = ² - х при цьому врахуємо, що функція в – парна і її графік – симетричний щодо осі ординат, у силу чого можна обмежитися побудовою тільки його правої частини ( х ≥ 0). Також урахуємо, що тричлен х² - 8х + 7 має коріння х = 1 і х = 7, при х = 0 в = 7, а при х = 4 – мінімум, рівний – 9. На малюнку: пунктирними прямими зображена парабола

в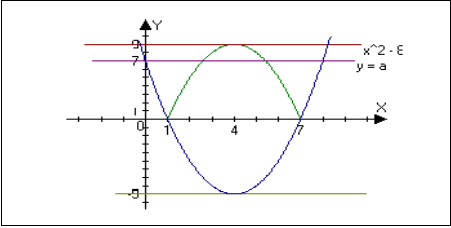  

 

 

 

 

 

 

 

 

 В  b=² – 8х + (1 < х < 7), отримана дзеркальним відбиттям щодо осі 0х частини параболи

х² - 8х + 7 при 1 < х < 7.

(Ескіз лівої частини графіка функції при х < 0 можна одержати, відбивши ескіз правої частини графіка симетрично щодо осі 0у).

Проводячи горизонталі в = а, а N, одержуємо k крапок її перетинання з лініями ескізу графіка. Маємо:

 

а	0	[1; 6]	7	8	9
к	4	8	7	6	4	2

Таким чином, а = k при а = 7.

Відповідь: 7.

 

Повідомлення учнів 10 класу:

 Презентація ІІІ групи 10 клас:

При підготовці до державної підсумкової атестації у 9 та 11 класі,

до зовнішнього незалежного оцінювання та до математичних олімпіад у 10 класі ми розв’язуємо задачі з параметрами на відшукання кількості розв’язків  рівняння з двома змінними, систем рівнянь з двома змінними.

Приклад 1 Знайти всі значення параметра , при яких система рівнянь 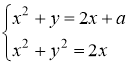має розв’язки.

Розв’язання. З першого рівняння системи знаходимо .

Це рівняння задає сім’ю парабол, які “ковзають" вершинами вздовж прямої . З другого рівняння знаходимо - коло з центром в точці (1, 0) радіуса 1.

З’ясуємо, при яких значення параметра сім’я парабол має спільні точки з колом.

Випадок дотику знайдемо з системи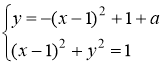, вимагаючи від системи мати один розв’язок. Одну спільну точку графіки мають при або . Якщо , то система має два розв’язки.

Відповідь: .

 

 

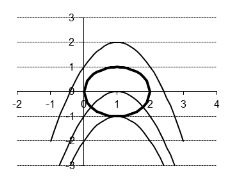
Приклад 2. При яких значеннях параметра а система має три розв’язки:

x² + (y-2)²=1

 y=| x| + a                                        має три розв’язки?

                               Розв’язання :

Побудуємо в одній системі координат графіки рівнянь системи:

                                                 y

 

 

 

                                     

                                

                                                          1

                                                       0     1               x                                              

                                                          

 

 

 

 

Графік першого рівняння - коло з центром у точці (0;2) і радіусом 1. Графік другого рівняння – прямий кут,  бісектриса якого лежить на осі ординат, а вершина якого рухається вздовж осі y, в залежності від значень параметра а.

Три розв’язки система рівнянь буде мати лише в тому випарку, якщо графіки рівнянь будуть зображені так, як на рис. 3.

Отже, при а=1.

Відповідь: при а=1.

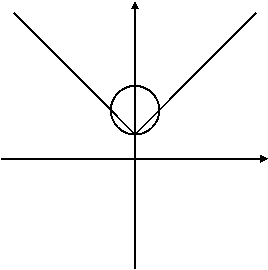
Приклад 3. Визначте кількість розв’язків системи

 

У = а + √х

2х+у-1=0

Розв’язання.

Графік другого рівняння буде пряма, першого - вітка параболи, що знаходиться в І четверті, і буде рухатись по осі ординат відносно параметра а.

Отже, побудуємо графіки цих рівнянь в одній системі координат.

 

Оскільки розміщення вітки параболи буде залежати від параметра а, то:

якщо а є(-∞; 1], то система має один корінь;

якщо а є(1; +∞),то система коренів не має.

Відповідь: 1) якщо а є(-∞; 1], то система                     має один корінь,

                  2) якщо а є(1; +∞),то система    

                      коренів не має.

 

 

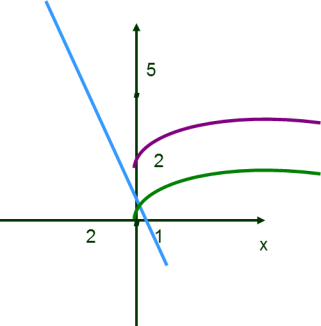
Приклад 4. Знайдіть усі значення параметра а, при яких система рівнянь

 x|+|y|=1

 x²+y²=a                   не має розв’язків

                                  Розв’язання

З другого рівняння системи бачимо, що при а ≤ 0 система не має розв’язків.

Розглянемо випадки, коли а>0.

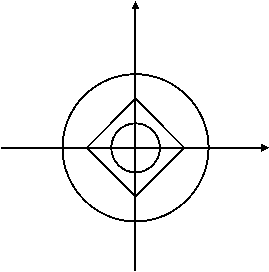
Графік першого рівняння  системи – квадрат з центром у початку координат і діагоналлю 2.

Графік другого рівняння – коло з центром у початку координат і радіусом  √а, а>0.

 

 

 

 

 

  .                                                    Y    

 

 

 

                                          1

 

                                         -1         0      1             x

                                                   

 

 

                                                   

 

 

 

 

 

 

Система не має розв’язків, якщо коло і квадрат не мають спільних точок. Це можливо тоді, коли:

√а>1, а>1

Або       _

√а < 1/√2 ,  а < 1/2

Відповідь: а є(-∞; ½) U(1;+∞).

Приклад 5. Знайти найменше ціле значення параметра а, при якому рівняння

 

(0 < х < ) має рішення.

 

Рішення: за умовою 1 > sinx > 0 1 < < + ,

 

1 > cosx > 0 1 < < + ,

 

Отже, 2 < а < + .

Зводячи обидві частини заданого рівняння у квадрат, маємо:

 

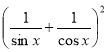= а² = а²

= а².

 

Уведемо змінну z = . Тоді вихідне рівняння прийме вид:

z² + 2z – а² = 0. Воно має рішення при будь-якому а, оскільки його дискримінант

D = 1 + а² позитивний при будь-якому а.

З огляду на, що 2 < а < + , містимо, що найменше ціле значення параметра а, при якому задане рівняння має рішення дорівнює 3.

Відповідь: 3.

 

 Приклад6. В залежності від значення параметра а розвязати систему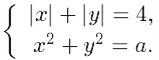

Розв’язання

З геометричної точки зору кількість розвязків системи – це число точок перетину при кожному фіксованому значенні параметра а кривих, заданих рівняннями системи.

Розглядуємо в першому рівнянні 4 випадки і розкриваючи модулі, отримаємо, що це рівняння задає квадрат (див. мал.). Друге рівняння – це сімейство кіл радіуса () з центром в початку координат. Якщо а=0, то коло вироджується в точку.

 

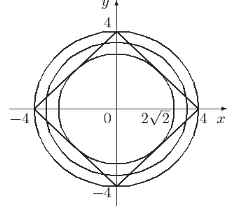
Із малюнка слідує, що коли коло дотикається квадрата всередині, тобто якщо (а=8) і якщо (а=16) (коло проходить через вершини квадрата) система має  4 розв’язки.

Якщо спільних точок у кола і квадрата 8.

Якщо розв’язків немає.

Відповідь.

Якщо  розв’язків немає;

Якщо  а=8 ; а=16: 4 розв’язки;

Якщо  :  8 розв’язків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 А тепер ми хочемо дізнатись вашу думку про проект.

o Як змінились ваші знання про задачі з параметрами?

o Розвитку яких рис характеру сприяв проект (самостійності, відповідальності, працелюбності)?

o Які пізнавальні процеси були задіяні під час проекту найбільше (мислення, пам’ять, уява, увага)?

o Якого життєвого досвіду ви набули (володіти собою, захищати свої знання, бути впевниними в собі)?

o Чи отримали ви задоволення від власної праці?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                 Для нотатків

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________                                                                  

 

                                 

                               ЛІТЕРАТУРА

 

1. Г.П.Бевз, В.Г.Бев., Алгебра, підручник для7класу загальноосвітніх навчальних закладів. Київ.Ззодіак-ЕКО”, 2007.
2. Інтерактивні технології на уроках математики. Упорядник І.С.Маркова- Ч.: Вид. група “Основа”, 2006.
3. Капіносов А.Н. основи технології навчання. Проектуємо урок математики.- Х.: Вид. група “Основа”, 2006.
4. Урок математики в сучасних технологіях: теорія і практика. Розвиток критичного мислення. Модульне навчання.- Х.: Вид. група “Основа”, 2007.
5. Урок математики в сучасних технологіях: теорія і практика. Метод проектів. Комп’ютерні технології. Розвивальне навчання. / Укладач І.С.Маркова- Х.: Вид. група “Основа”, “Тріада+”, 2007.
6. Проектна діяльність у школі./ Упорядник М. Голубенко – К. Шк. Світ,-128с.
7. М.І.Шкіль, З.І.Слепкань, О.С.Дубинчук. Алгебра і початки аналізу: 10-11 кл. – К: 1995.
8. В.В.Ясінський. Математика. Навчальний посібник. За ред.., В.С.Мельника – К.:2004-200с.
9. Г.А.Ястребинецький. Задачі з параметрами: - М.: Просвещение, 1986 – 128с.
10. Задачі з параметрами. Проект програми, підручник факультативного курсу для 9 класу. Укладачі: вчителі математики Хмельницької СЗШ №8 Нагурнік Л.О., Кравчук Г.Т., 2010.
11. Г.А.Ястребинецький Рівняння й нерівності, що містять параметри. – К., 2004
12. В.В.Лікоть Задачі з параметрами, - К., 2003р.
13. Т.Л.Корнієнко, В.І.Фіготіна. Алгебра. Дворівнева методика викладання. 7 клас / за ред.. І.С.Маркової. Х.: - Видавництво “Ранок”. Веста, 2007.