Квадра́тне рівня́ння — алгебраїчне рівняння виду

 де .

Загальним розв'язком цього рівняння є формула

Квадратні рівняння є різновидом рівнянь другого степеня з однією змінною. Числа  — його коефіцієнти, при чому  також називається першим або старшим коефіцієнтом,  — другим,  — вільним членом. Будь-яке квадратне рівняння має

• або два різних дійсних корені,
• або два однакові дійсних корені (тобто, по суті, один),
• або взагалі не має дійсних коренів, а має два комплексні корені.

(Зазвичай, коли кажуть, що коренів немає, то мається на увазі, що немає дійсних коренів: в такому разі обидва корені є комплексними. Вони позначаються як  та або, якщо йдеться про обидва корені одночасно, то  В деякій літературі зустрічається ще й таке позначення:  і .)

Неповні квадратні рівняння

Згідно з означенням, перший коефіцієнт квадратного рівняння не може дорівнювати нулю: якщо , то  перетворюється у лінійне рівняння . Якщо хоч один коефіцієнт  або  дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів:

• ;
• ;
• .

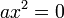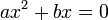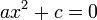Розв'язування неповних квадратних рівнянь

• Рівняння виду 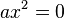 рівносильне рівнянню  і тому завжди має тільки один корінь .
• Рівняння виду 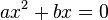 розв'язується винесенням за дужки 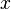: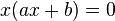.  Таке рівняння має два корені: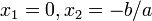 
• Квадратне рівняння виду 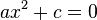 рівносильне рівнянню 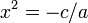. Якщо 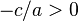, воно має два дійсних розв'язки, якщо  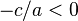— жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то  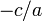додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число  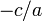від'ємне і  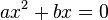не має дійсних коренів

Повне квадратне рівняння

Повним називається таке квадратне рівняння, у якому жодний з коефіцієнтів  не дорівнює нулю.

Дискримінант[

Повні квадратні рівняння розв'язуються за допомогою дискриміна́нта (лат. diskriminans — розрізняючий), який позначається латинською літерою .

Помноживши обидві частини рівняння  на , дістанемо:

Вираз і є дискримінантом:

Розв'язування повних квадратних рівнянь

Якщо , то

,

Якщо , то ,звідки  — єдиний корінь (правильніше - два однакові корені)

У випадку, якщо дискримінант менший за нуль, то дане рівняння не має дійсних коренів.

Якщо коефіцієнти в рівнянні мають великі числові значення для уникнення довгих розрахунків можна скористатися формулою:

 де :

Квадратне рівняння

Підготувала Сімейко А.І.

Гімназія нових технологій навчання

Кіровоградської міської ради

Кіровоградської області