Буклет на тему "Многокутники"

Многокутники

Об’єднання простої замкненої ламаної та її внутрішньої області називається многокутником.

Найпростіші представники многокутників  

1.Трикутник

2.Трапецiя

3.Ромб

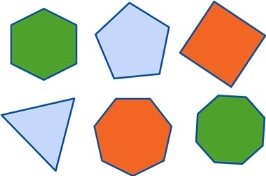
Опуклий многокутник

Многокутник називається опуклим, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону. При цьому сама пряма вважається такою, що належить півплощині.

Елементи чотирикутника

Ланки ламаної називаються сторонами многокутника. Точки, в яких збігаються дві суміжні ланки, називаються вершинами многокутника. Кути, утворені двома суміжними сторонами многокутника, називаються внутрішніми кутами многокутника. Кути, суміжні з внутрішніми кутами многокутника, називаються його зовнішніми кутами. Відрізок, що з’єднує дві вершини, які не належать одній з його сторін називається діагоналлю. Сума довжин усіх сторін многокутника називається його периметром. 

Правильні многокутники

Правильним називається опуклий многокутник, в якого всі кути і всі сторони рівні. Найпростіші приклади правильних многокутників є рівносторонній трикутник, квадрат. 

Вписані та описані многокутники 

Многокутник називається вписаним у коло, якщо всі його вершини лежать на колі (коло описане). Многокутник називається описаним, якщо всі сторони многокутника дотикаються до цього кола (коло вписане) Вписане й описане кола правильного многокутника мають один і той самий центр.

Елементи правильних многокутників

 Правильні однойменні многокутники подібні, їх сторони відносяться як апофеми або радіуси, а площі відносяться як квадрати апофем або радіусів. Радіусами правильного многокутника називаються відрізки , що сполучають його центр з вершинами. Апофемами правильного многокутника називаються відрізки перпендикулярів, опущених з його центра до перетину зі сторонами.

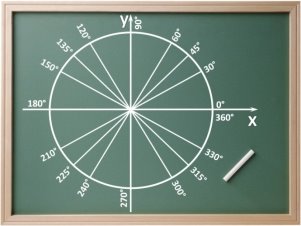
Многокутники

Підготувала Сімейко А.І.

Гімназія нових технологій навчання

Кіровоградської міської ради

Кіровоградської області