Ознаки подібності трикутників

Теорема 1. Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники подібні.
Теорема 2. Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то трикутники подібні.
Теорема 3. Якщо сторони одного трикутника пропорційні сторонам другого трикутника, то такі трикутники по­дібні.
 

Пряма, яка паралельна стороні трикутника і яка перетинає дві інші його сторони, відтинає від нього трикутник, подібний даному.

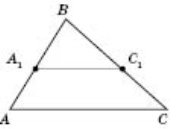
 У подібних трикутників відповідні елементи (висоти, медіани, бісектриси тощо) відносяться як відповідні сторони.
У подібних трикутників периметри відносяться як відповідні сторони.

 Якщо О — точка перетину діагоналей трапеції ABCD, то .
На рисунку в трапеції ABCD:.

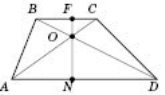
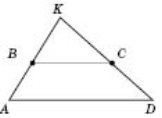
Якщо продовження бічих сторін трапеції ABCD перетинаються в точці K, то ∆ВКС~∆АКD (див. рисунок).
.

Ознаки подібності прямокутних трикутників

За гострим кутом.                                                  Якщо прямокутні трикутники мають по рівному гострому куту, то такі трикутники подібні.

За двома пропорційними катетами. Якщо катети одного прямокутного трикутника пропорційні катетам другого прямокутного трикутника, то такі трикутники подібні. 

За пропорційними катетом і гіпотенузою.                                                                Якщо катет і гіпотенуза одного прямокутного трикутника пропорційні катету і гіпотенузі другого прямокутного трикутника, то такі трикутники подібні.                                                                             

Теорема Піфагора

Теорема звучить так:

Позначивши довжину гіпотенузи трикутника як c, а довжини катетів як a та b, отримаємо такі формули:  

Властивостi

Теорема, оберена до теореми Піфагора):

Піфагорові  3 4 5;  6 8 10; 9 12 15;             

трійки: 5 12 13; 10 24 26

Нехай ABC — прямокутний трикутник, в якому кут C прямий, як показано на малюнку. Проведемо висоту з точки C, і назвемо H-точку перетину з стороною AB. Утворений трикутник ACH подібний трикутнику ABC, оскільки вони обидва прямокутні (за визначенням висоти), і в них спільний кут A, очевидно третій кут буде в цих трикутників також однаковий.

Іншими словами, теорема Піфагора:

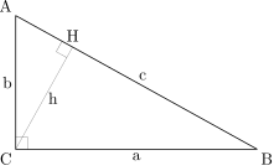
Метричні співвідношення

·    · c

h   = 

Ознаки подібності трикутників.Теорема Пiфагора

Підготувала Сімейко А.І.

Гімназія нових технологій навчання

Кіровоградської міської ради

Кіровоградської області