Числові послідовності. Властивості числових послідовностей.
Тема уроку. Числові послідовності. Властивості числових послідовностей.
Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, п-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття.
Тип уроку: засвоєння знань, вироблення вмінь.
Наочність та обладнання: опорний конспект № 28.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
На уроці розбираються найскладніші питання контрольної роботи, які учні не могли опрацювати вдома.
ІІІ. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
На цьому етапі уроку вчителю слід навести якомога більше числових послідовностей, з якими учні можуть зустрічатися в повсякденному житті, а також при вивченні основ наук. Таким чином учнів підготовляють до сприйняття думки про те, що предметом вивчення математики є не тільки вирази, рівняння, нерівності тощо; математика вивчає також результати спостережень за реальними фізичними, хімічними процесами, кліматичними явищами, які виражаються у вигляді рядів чисел, кожне з яких стоїть у цьому записі на строго визначеному місці. Після цього цілком логічно сформулювати завдання: вивчити питання про ці «ряди чисел», а також можливості подальшого застосування цих понять на практиці. Таким чином формулюється в загальному вигляді основна дидактична мета уроку.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Знайдіть значення виразу:
1) -2,6 + 0,5; 2) -2,1 : (-0,01); 3) (0,45)4 : 0,418;
4) ![]() ; 5)
; 5) 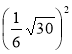 ; 6)
; 6) ![]() ;
;
7) (3 – ![]() )(3 +
)(3 + ![]() ).
).
-
Спростіть вираз:
1) (4b + 1) – (3 – b); 2)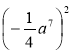 ; 3) (2x – 1)(х – 2);
; 3) (2x – 1)(х – 2);
4) а5 ∙ а12 : а16; 5) ![]() ; 6) 3x2y5 ∙ (-x3y2).
; 6) 3x2y5 ∙ (-x3y2).
- Знайдіть значення виразу:
1) х + 10у при х = 1,5, у = -![]() ; 2) 2x2 + 1 при х = -4;
; 2) 2x2 + 1 при х = -4;
3) х2 + 6х – 2 при х = 3.
V. Формування знань
План вивчення нового матеріалу
- Означення числової послідовності. Поняття члена послідовності.
- Види числових послідовностей:
1) залежно від кількості її членів;
2) залежно від тенденції її членів (зростаюча, спадна, така, що не є зростаючою або спадною).
- Способи задання числових послідовностей:
1) переліком її членів;
2) описом її членів;
3) таблицею;
4) формулою (п-го члена);
5) рекурентною формулою.
Опорний конспект № 28
|
Числовою послідовністю називається функція, яка задана на множині всіх натуральних чисел або на множині перших п натуральних чисел. |
|||||||
|
Числова послідовність позначається так: (ап): а1; а2; а3; ...; ап. Кожне число ап — п-й член послідовності; п — номер члена. |
|||||||
|
Види числових послідовностей |
|||||||
|
1. Якщо кількість членів п послідовності (ап) скінченна, то (ап) — скінченна послідовність. Якщо кількість членів п послідовності (ап) нескінченна, то (ап) — нескінченна послідовність. Приклади: а) послідовність (ап) натуральних чисел нескінченна; б) послідовність (ап) коренів рівняння (х – 1)(х – 2)(х + 3) = 0 скінченна. |
|||||||
|
2. Якщо кожний наступний член послідовності, починаючи з другого, більший за попередній, то послідовність є зростаючою. Якщо кожний член послідовності, починаючи з другого, менший від попереднього, то послідовність є спадною. |
|||||||
|
Приклади: а) (ап): 1; 2; 3; ... — послідовність натуральних чисел є зростаючою; б) (bп): -1; -2; -3; ... — послідовність цілих від'ємних чисел є спадною. |
|||||||
|
Способи задання числових послідовностей: 1) описом знаходження її членів. Приклад. Числова послідовність дільників числа 15, записаних у порядку зростання: (ап): а1= 1; а2 = 3; а3 = 5; ...; а4 = 15; |
|||||||
|
2) переліком її членів. Приклад. (bn): 54; 1; 33; 27, тоді а1 = 54; а2 = 1; а3 = 33; а4 = 27; |
|||||||
|
3) таблицею. Приклад. |
|||||||
|
|
п |
1 |
2 |
3 |
4 |
5 |
|
|
|
ап |
-2 |
1 |
-4 |
1 |
-6 |
|
|
|
|||||||
|
Тоді а1 = -2; а2 = 1; а3 = - 4; а4 = 1; а5 = 6; |
|||||||
|
4) формулою п-го члена. Приклад. ап = п2 – 1, тоді а1 = 12 – 1 = 0; а2 = 22 – 1 = 3; а3 = 32 – 1 = 8 і т.д.; |
|||||||
|
5) рекурентною формулою. Приклад. ап = ап-1 ∙ ап-2, якщо а1 = 1; а2 = 2, тоді а1 = 1; а2 = 2; а3 = а1 ∙ а2 = 2; а4 = а2 ∙ а3 = 2 ∙ 2 = 4; а5 = а3 ∙ а4 = 4 ∙ 2 = 8. |
|||||||
Методичний коментар
Матеріал цього уроку є допоміжним для вивчення матеріалу наступних уроків, тому розглядається лише в обсязі, необхідному для вивчення арифметичної та геометричної прогресій. Учні мають на прикладах числових послідовностей засвоїти необхідну для подальшого вивчення матеріалу термінологію: послідовність, член послідовності, номер члена послідовності, формула п-го члена послідовності, рекурентна формула.
VI. Формування вмінь
Усні вправи
-
Дано послідовність: 0,1; 7; 0,2; 8; 0,3; 9. Укажіть:
- скільки членів має ця послідовність;
- третій член послідовності;
- який номер має член послідовності, що дорівнює 0,3;
- який член послідовності є наступним за числом 8; попереднім до числа 7.
- Послідовність (хп) задано формулою хп = п + 5. Укажіть перші три члени цієї послідовності. Чи є ця послідовність зростаючою? нескінченною?
Письмові вправи
Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:
- для послідовності записати номер члена, що передує члену із заданим номером; є наступним за членом із заданим номером;
- знайти перші кілька членів послідовності, заданої: а) описом; б) формулою п-го члена; в) рекурентно;
- скласти формулу п-го члена для послідовності, заданої описом або переліком її членів;
- знайти номер члена послідовності (чи є дане число членом послідовності), заданої формулою п-го члена.
Методичний коментар
Усі вправи, які заплановано розв'язати на уроці, мають бути спрямовані на закріплення вивченої термінології, а також на вироблення вмінь працювати з формулою п-го члена числової послідовності (яку можна використовувати як прямо, для обчислення члена числової послідовності із заданим номером, так і для розв'язування оберненої задачі — для заданого числа, що є членом числової послідовності, знайти його номер). Також слід приділити увагу виробленню вмінь учнів працювати з рекурентними формулами, специфіка яких полягає в тому, що для обчислення члена послідовності, що стоїть на певному місці, слід у формулу підставляти не його номер, а попередній (попередні члени). Під час виконання всіх вправ на обчислення звертаємо увагу на відпрацювання обчислювальних навичок учнів.
VII. Підсумки уроку
Контрольні запитання
- Наведіть приклади числових послідовностей.
- Наведіть приклад числової послідовності: 1) скінченної; 2) нескінченної.
- Наведіть приклад послідовності, заданої формулою п-го члена. Назвіть який-небудь член цієї послідовності.
- Наведіть приклад послідовності, заданої рекурентною формулою.
VIII. Домашнє завдання
- Вивчити означення понять, розглянутих на уроці (див. опорний конспект № 28).
- Розв'язати вправи, аналогічні за змістом та рівнем складності виконаним на уроці.
- Повторити перетворення раціональних виразів.


про публікацію авторської розробки
Додати розробку
