Сума перших п членів арифметичної прогресії.

Тема уроку. Сума перших п членів арифметичної прогресії.

Мета уроку: домогтися засвоєння учнями формул суми перших п членів арифметичної прогресії через перший і п-й члени та через перший член і різницю арифметичної прогресії. Виробити вміння: записувати вивчені формули залежно від умови задач, а також використовувати їх для розв'язування за­дач, що передбачають обчислення суми перших п членів арифметичної прогресії.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання: опорний конспект № 31, роздавальний ма­теріал (картки з розв'язаннями домашньої самостійної роботи).

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Учитель збирає зошити учнів із виконаною домашньою са­мостійною роботою. Найбільш складні завдання розглядаються. У разі необхідності правильні розв'язання у вигляді роздаваль­ного матеріалу роздаються учням для самостійного опрацювання вдома.

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів

Для усвідомлення учнями необхідності вивчення питання про формулу суми перших п членів арифметичної прогресії можна за­пропонувати їм одну із цікавих задач на обчислення такої суми (наприклад, широко відома задача на обчислення суми перших 100 натуральних чисел). Під час обговорення умови задачі учні приходять до усвідомлення того, що мовою математики умова за­дачі звучить так: «Знайти суму перших 100 членів арифметич­ної прогресії». Розглянувши приклади інших задач цього виду, формулюється узагальнена умова задачі: «Як знайти суму перших кількох членів арифметичної прогресії»; після цього формулюєть­ся мета: вивести формулу для обчислення суми перших п членів арифметичної прогресії; виробити вміння її застосовувати при розв'язуванні задач.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Назвіть перший член і різницю арифметичної прогресії, що задана формулою b_п = 115п – 4. Запишіть формулу n-го члена цієї арифметичної прогресії.
2. Відомо, що в скінченній арифметичній прогресії сума першого й останнього членів дорівнює 10. Чому дорівнює сума другого і передостаннього членів?
3. Знайдіть:
   1. значення функції, що задана формулою у = 4х – 3, для всіх цілих значень змінної х з проміжку (2; 5];
   2. значення аргументу, при яких значення функції у = х² – 5 дорівнює 0; 4; -5.

V. Формування знань

План вивчення нового матеріалу

1. Формула суми перших п членів арифметичної прогресії через перший і   n-й члени.
2. Формула суми перших п членів арифметичної прогресії через перший член і різницю арифметичної прогресії.
3. Приклади розв'язування задач.

Опорний конспект № 31

Методичний коментар

Вивчення матеріалу уроку починається з виведення формули суми перших п членів арифметичної прогресії через перший і л-й члени, для чого використовується властивість скінченної арифме­тичної прогресії (про те, що сума кожної пари членів, рівновіддалених від її кінців, дорівнює сумі крайніх членів цієї прогресії) та досить прості міркування про кількість пар чисел, що містять­ся в ряді п чисел. Друга формула для обчислення суми перших п членів арифметичної прогресії через перший її член і різницю виводиться із застосуванням до виведеної формули вивченої ра­ніше формули п-го члена арифметичної прогресії. Після вивчен­ня обох формул слід наголосити на тому, що вибір формули для розв'язування конкретної задачі зумовлений даними задачі (при­клади розв’язування типових задач наведені в опорному конспекті № 31).

VI. Формування вмінь

Усні вправи

1. Задана скінченна послідовність: (а_n): 2; -1; 5; -2; 9; -3; 15; -4. Знайдіть суму:

1) перших двох її членів;

2) перших п'яти її членів;

3) усіх її членів.

1. Знайдіть суму перших тридцяти членів арифметичної прогре­сії (х_п), у якої х₁ = 5, х₃₀ = 15.
2. Знайдіть суму перших десяти членів арифметичної прогре­сії (у_п), у якої  y₁ = 5, d = 3, заповнивши пропуски у формулі .

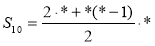Письмові вправи

Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:

1. за однією з вивчених формул знайти (обчислити) суму перших п членів арифметичної прогресії;
2. розв'язати задачі, що передбачають пряме застосування ви­вчених формул (в умові задач напряму не сказано, що шука­на сума є сумою арифметичної прогресії), наприклад, знайти суму перших 50 натуральних чисел або знайти суму парних натуральних чисел від 0, не більших за 100, і т. д.;
3. задачі на застосування вивчених формул для відшукання не­відомих першого члена, або різниці, або кількості п членів арифметичної прогресії за відомою за умовою сумою її перших членів;
4. на повторення: задачі на застосування вивчених властивостей і формул арифметичної прогресії.

Методичний коментар

При розв'язуванні вправ закріплюється знання формул та усві­домлення відмінності ситуацій, у яких виправдане застосування однієї з вивчених формул, а також формуються вміння працювати із вивченими формулами в різних напрямках: як для відшукання значення суми арифметичної прогресії, так і для відшукання за даною сумою інших даних (першого члена арифметичної прогресії, або її різниці, або кількості перших членів, для яких відома їхня сума). Крім цього продовжується робота із закріплення ключових моментів, над якими розпочалась робота на попередніх уроках: як перевірити, чи є задана послідовність арифметичною прогре­сією (за означенням, або за характеристичною властивістю, або за теоремою, залежно від умови); як знайти різницю арифметич­ної прогресії (від будь-якого члена, починаючи з другого, відняти попередній до нього член); як знайти наступний за даним член арифметичної прогресії (знайти різницю арифметичної прогресії й додати її до даного члена).

VII. Підсумки уроку

Контрольні запитання

1. За якою формулою можна обчислити суму перших ста членів арифметичної прогресії, якщо відомі:

1) а₁ і а₁₀₀;   2) а₁ і d;  3) а₁ і а₂?

2. Чи можна за формулою 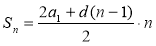обчислити суму перших десяти членів послідовності:
   1.   (а_n): 2; 3; 4; 5; 6; ...;
   2.   (а_n): 2; 4; 8; 16; 32; ...;
   3.   (а_п): n; 3n; 5n; 7n; 9n; 

VIII. Домашнє завдання

1. Вивчити формули (див. опорний конспект № 31).
2. Розв'язати вправи, аналогічні за змістом та рівнем складності виконаним на уроці;
3. Повторити: означення числової послідовності, формули, вивче­ні в темі «Арифметична прогресія» та властивості натурально­го ряду чисел (зокрема, скільки натуральних чисел міститься в натуральному ряді з га по гаг чисел включно).