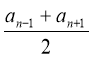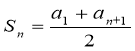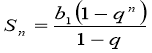Цикл уроків алгебри для 9 класу з теми "Числові послідовності. Арифметична та геометрична прогресії"

Тема: Геометрична прогресія, її властивості.

Мета: Сформувати поняття геометричної прогресії, знаменника геометричної прогресії,  властивостей членів геометричної прогресії; розвинути логічне мислення учнів, пам’ять, увагу; виховати старанність, уважність,  інтерес до геометрії.

Тип уроку: комбінований.

Обладнання: таблиця.

Хід уроку.

I. Організаційна частина. ( перевіряю готовність учнів до уроку)

II. Актуалізація опорних знань учнів, перевірка домашнього завдання.

 Учні обмінюються зошитами. Далі по черзі один читає розв'язання вправи, решта перевіряє це розв'язання в зошиті сусіда. Той, в чиєму зошиті виявлено помилку, виходить до дошки (з книжкою) і пояснює, як він розв'язував. З'ясовується природа помилки. Повторюється відповідний теоретичний матеріал.

1. Два учні відтворюють розв'язання домашніх вправ № 239, 241,
   інші пишуть математичний диктант.
2. Математичний   диктант.

• Запишіть формулу п-го члена арифметичної прогресії.

• Запишіть формулу суми п перших членів арифметичної
  прогресії.
• Скільки членів містить скінченна арифметична прогресія 3, 6, 9, ., 273.
• Запишіть формулу n-го члена арифметичної прогресії 3, 6, 9, ..., 273.
• Знайдіть суму чисел 3 + 6 + 9 + ... +273, якщо її доданки є послідовними членами арифметичної прогресії.
• Запишіть формулу для знаходження суми п перших членів
  арифметичної прогресії 3, 6, 9, ..., 273, ... .

3. Заслухати відповіді учнів, перевірити математичний диктант
та відповісти на запитання, які виникли в учнів.

III. Формування поняття геометричної прогресії та вивчення властивостей членів геометричної прогресії.

Випишемо декілька членів послідовності (b_n ), якщо b₁ = 3, Ь_п+1 = 2Ь_n, п є N:3, 6, 12, 24, 48, 96, 192, ... .

Кожен член цієї послідовності, починаючи з другого, одержу­ють множенням попереднього члена на 2.

Означення.

Геометричною прогресією називається послідовність відмінних від нуля чисел, кожний член якої, починаючи з дру­гого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число позначають q, називають знаменником геометричної прогресії.

Інакше кажучи, послідовність (b_п) — геометрична прогресія, якщо для будь-якого натурального п виконується умова:

Із означення геометричної прогресії випливає, що q = .

Щоб задати геометричну прогресію, досить вказати її перший член b₁ і знаменник q. Члени геометричної прогресії мають таку властивість.

Теорема 1. Квадрат кожного члена починаючи з другого, дорівнює добутку двох сусідніх з ним членів, тобто

 Справедлива і теорема, обернена до доведеної.

Теорема 2. Якщо в послідовності члени не дорівнюють нулю і квадрат кожного члена, починаючи з другого, дорівнює добут­ку двох сусідніх з ним членів, то така послідовність — геометрична прогресія.

Оскільки частка від ділення кожного члена послідовності на попередній йому член — одне й те саме число, то ця послідов­ність — геометрична прогресія.

Для будь-якої прогресії з додатними членами доведені теоре­ми можна сформулювати в такій формі.

Кожний член геометричної прогресії, починаючи з другого, дорівнює середньому геометричному двох сусідніх з ним членів, тобто

, n>1

Якщо кожний член числової послідовності з додатними члена-,ми, починаючи з другого, дорівнює середньому геометричному І сусідніх з ним членів, то така послідовність є геометричною про­гресією.

Сформульовані твердження пояснюють назву геометричної прогресії.

IV. Закріплення нового матеріалу.

 Виконання вправ:

1. Чому дорівнює перший член і знаменник геометричної про­гресії:

a) 2, 8, 32, 128,...;   б) 1,

в) , 1, -12,144, ...;  _Г) 7, 7, 7, ...;

д) 3, , ...;     е) 5, -, 10, ... .

2. Запишіть перші п'ять членів геометричної прогресії, якщо:
   а) Ь₁ = 2, q = 3; б) Ь₁ = 4, q = -2;

в) b_l = 4, q = ; г) Ь₁ = -3, q = -;

д) b_l  = 1, q = ; е) b_l = , q = .

3. Вправи № 514,518

4.  Знайдіть п'ятий член і знаменник геометричної прогресії, якщо;

а)b₄= ,  b₆= 81;           б) b₄=,  b₆ = 81;

в) b₄ - 9, b₆  = 3;                г) b₄ =, b₆ = .

5. Між наведеними парами чисел вставте додатне число так, щоб утворилось три послідовні члени геометричної прогресії:

 а) 4 і 9;                      б) 3 і 4;                     в) і .

V.Домашнє завдання

§ 11, п.11.1  № 515, 519, 521(а,в)*

Тема:  Формула n-го члена геометричної прогресії.

Мета: вивести формулу n-го члена геометричної прогресії та сфор­мувати в учнів уміння застосовувати формулу n-го члена гео­метричної прогресії до розв'язування задач, розвинути логічне мислення учнів, пам’ять, увагу; виховати старанність, уважність,  інтерес до геометрії

Тип уроку: комбінований.

Обладнання: таблиця.

Хід уроку.

I. Організаційна частина. ( перевіряю готовність учнів до уроку)

II. Актуалізація опорних знань учнів, перевірка домашнього завдання.

1.  Перевірити наявність виконаних домашніх завдань та відпо­вісти на запитання, які виникли в учнів при їх виконанні.

2.  Фронтальна  бесіда

Запитання до класу

•   Яка послідовність називається геометричною прогресією? Наведіть приклади.

• Які із наведених скінченних послідовностей є геометричною прогресією: а) 1, 4, 7, 10, 13;       б) 1, 3, 9, 27, 81;

в) 1, ;   г) 1, 3, 27, 81, 243?

• Назвіть перші п'ять членів геометричної прогресії, якщо:

 а) Ь₁ =9, q = 3; б) Ь₁ = 9, q = 1/3;

• Знайдіть знаменник геометричної прогресії, якщо:

а) b₃₀ = 3О, b₃₁ = 40;     б) b_n = 35,  b_п-1= 105.

• Сформулюйте властивість членів геометричної прогресії.

•3найдіть'невідоме число, якщо дані три числа є послідов­ними членами геометричної прогресії: а) , х, 32;                            б) -7, х, -28.

 

 

III. Вивчення нового матеріалу

  Знаючи перший член і знаменник геометричної прогресії, можна знайти будь-який її член, обчислюючи послідовно другий, третій, четвертий і так далі члени. Проте, щоб знайти член прогресії з великим номером, такий спосіб незручний. За означенням геометричної прогресії:

b₂=b₁q;

b₃=b₂;

;

;

Легко помітити, що для будь-якого натурального п справедлива формула:

тобто n-й член геометричної прогресії одержимо, якщо перший член помножимо (п - 1) разів на число q.

Цю формулу називають формулою п-го члена геометричної прогресії.

Розглянемо приклади розв'язування задач з використанням цієї формули. Задача 1. Знайдіть сьомий член геометричної прогресії, якщо

b_l = 64, q =.

Розв’язання: За формулою знаходимо 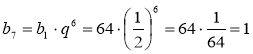.   Відповідь. 1.

Задача 2. Знайдіть формулу п-го члена геометричної прогресії 3, 9, 27,

Розв'язання: Знаменник геометричної прогресії дорівнює q =9/3 = 3.

За формулою при b_l =  3 і q = 3 знаходимо:

                    = 3 • 3^n-1=3ⁿ.  Відповідь .Ь_п = 3ⁿ.

Задача 3. Знайдіть знаменник геометричної прогресії, у якій

b₁ = 2, b₅= 162.

Розв'язання:  За формулою маємо 162 = 2 • q⁴, тоді

q⁴ =162/2= 81, звідси q= 3 або q = -3.

Відповідь, q = 3 або q = -3.

Задача 4. Число 512 є членом геометричної прогресії 8, 16, 32,....  Знайдіть номер цього члена.

Розв'язання: Нехай п — шукане число. Оскільки Ь₁ = 8, a q = 16/8 = 2, то за формулою   маємо:

512=8*2^n-1;  2^n-1 = 64;  2^n-1  = 2⁶; п - І = 6, п = 7. Відповідь, п =7.

IV. Закріплення нового матеріалу.

 Виконання вправ:

1. Вправи №522, 524

2.  Знайдіть п'ятий член геометричної прогресії, якщо:

a) b₂= , b₇=81;      б) Ь₃ =-2, Ь₆ =-16;        в)Ь₂ = 3, Ь₄=1.

3.  Знайдіть п'ятий і перший члени геометричної прогресії, якщо:

а) Ь₄ = 5, b₆ = 20;        б) Ь₄ = -1/5, .

4.  Між числами 2 і 162 вставте такі три числа, які разом із да­ними числами утворюють геометричну прогресію.

5. Геометрична прогресія Ь_п складається із чотирьох членів: 2, Ь₂, bз, . Знайдіть b₂, b₃.

6.  Вправа № 527

V. Домашнє завдання.

 § 11, №№ 533, 525, 526

VІ. Підсумок уроку

1. Запишіть формулу n-го члена геометричної прогресії.

2. У геометричній прогресії перший член дорівнює 8, другий  4.Знайдіть:

а) знаменник q прогресії; б) третій член прогресії;

в) п'ятий член прогресії; г). номер члена прогресії, який дорівнює 1/8.

 

 

Тема: Сума перших п членів геометричної прогресії.

 Мета: вивести  формулу суми перших п членів геометричної прогресії, сформувати в учнів уміння застосовувати виведену фор­мулу до розв'язування задач, розвинути логічне мислення учнів, пам’ять, увагу; виховати старанність, уважність,  інтерес до геометрії

Тип уроку: комбінований.

Обладнання: таблиця.

Хід уроку.

I. Організаційна частина. ( перевіряю готовність учнів до уроку)

II. Актуалізація опорних знань учнів, перевірка домашнього завдання.

1.  Правильність виконання домашнього завдання перевірити за записами, зробленими на дошці до уроку

2. Самостійна  робота.

І варіант

1. Знайдіть сьомий член геометричної прогресії, якщо b₁ = 16, q=1/2.

2. Знайдіть перший член геометричної прогресії,

якщо b₅=17, q = -2

3. Знайдіть знаменник геометричної прогресії, якщо b₅ = -6, Ь₇ = -54.

4. Знайдіть сьомий член і знаменник геометричної про­гресії з додатними членами, якщо b₆ = , b₈ = 81.    

II варіант

1.  Знайдіть шостий член геометричної прогресії, якщо b₁ = 125, q = 0,2.                                               

2.  Знайдіть перший член геометричної прогресії, якщо b₆ = 3, q = 3.                                                      

3.Знайдіть знаменник геометричної прогресії, як­що b₆ = 25, b₈ = 9. 

4. Знайдіть сьомий член і знаменник геометричної про­гресії з додатними членами, якщо b₄ = 9, b₆ = 4.    

III. Сприйняття та усвідомлення нового матеріалу

 Існує легенда, згідно з якою винахідник шахів попросив у нагороду за свій винахід стільки пшеничних зерен, скільки їх буде, якщо на першу клітинку шахівниці покласти одну зернину, на другу — дві, на третю — чотири і так далі до 64 клітини. Скільки зерен повинен був одержати винахідник шахів?

Число зерен, про які йдеться в задачі, є сумою шестидесяти чотирьох членів геометричної прогресії, перший член якої дорівнює 1, а знаменник дорівнює 2. Позначимо цю суму через S: S = 1 + 2 + 2² + 2³ + ... + 2⁶² + 2⁶³.

Помножимо обидві частини записаної рівності на знаменник прогресії, одержимо:

2S = 2 + 2² + 2³ + 2⁴ + ... + 2⁶³ + 2⁶⁴. Віднімемо почленно із другої рівності першу і проведемо спрощення:

2S - S = (2 + 2² + 2³ + 2⁴ + ... + 2⁶³ + 2⁶⁴) -(1 + 2 + 2² + 2³ + ... + 2⁶³),

S = 2⁶⁴ - 1,

S = 18446 744 073 709 551 615.

Можна підрахувати, що маса такого числа пшеничних зерен більша за триліон тонн. Якби таке число зерен рівномірно розсипати по всій земній суші, то утворився б прошарок пшениці завтовшки близько 9 мм. Такої кількості пшениці людство не виростило до сьогоднішнього часу. Виведемо тепер формулу суми п перших членів довільної геометричної прогресії.

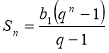, Отже, сума п перших членів геометричної прогресії зі знаменни­ком дорівнює: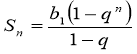

 Якщо q= 1, то S_n = b₁ + b₁. +... +  b₁= b₁n, тобто S_n =b₁п.

Розглянемо приклади розв'язання задач з використанням цієї формули.

Задача 1. Знайдіть суму шести перших членів геометричної прогресії .....

Розв'язання: Оскільки Ь₁ =,   q = . За формулою суми п перших членів геометричної прогресії маємо:

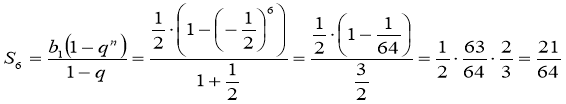
Відповідь.

Задача 2. Знайдіть число членів геометричної прогресії, якщо

S_n = 189, b₁ = 3, q= 2.

Розв'язання:

Скористаємося формулою суми п перших членів геометрич­ної прогресії, одержимо:

;  1 – 2ⁿ= -63; звідси 2ⁿ=2⁶, отже n=6

IV. Закріплення нового матеріалу.

 Виконання вправ:

Вправи № 530, 535

V. Домашнє завдання.

§ 11, п.11.2, №№ 531, 534, 538

VI. Підведення підсумків уроку.

Запитання до класу

1. За якою формулою можна знайти суму п перших членів геометричної прогресії, якщо q≠1?

2. Чому дорівнює сума п перших членів геометричної прогресії,
якщо q = 1?

 

Тема: Нескінченна спадна геометрична прогресія зі знаменником

|q| < 1 та її сума.

Мета: Познайомити учнів з нескінченними спадними геометричними прогресіями зі знаменником |q| < 1. Ввести поняття суми не­скінченної спадної геометричної прогресії, вивести формулу для знаходження суми. Формування в учнів уміння застосовувати ви­ведену формулу до розв'язування вправ, розвивати логічне мислення учнів, виховувати любов до геометрії

Тип уроку: комбінований.

Хід уроку.

I. Організаційна частина. ( перевіряю готовність учнів до уроку)

II. Актуалізація опорних знань учнів, перевірка домашнього завдання.

1. Перевірити наявність виконаних домашніх завдань та відпо­вісти на запитання, які виникли в учнів при їх виконанні. Уч­ні перевіряють свої розв'язання за записами, зробленими на дошці до початку уроку.

III. Формування поняття нескінченної спадної геометричної прогресії та її суми

Розглянемо квадрат зі стороною 1. Візьмемо його половину, потім половину частини, що залишилася, і т. д. . Площі заштрихованих прямокутників утворюють геометричну прогресію 1/2, 1/4, 1/8 , 1/16 , 1/32 , 1/64, ...знаменник якої дорівнює g=1/2.

Заштрихо­вані прямокутники заповнюють увесь квадрат. Доречно вважати, що сума площ всіх заштрихованих прямокут­ників дорівнює 1, тобто

У лівій частині цієї рівності за­писано суму нескінченного числа доданків.

До сьогоднішнього уроку ми розглядали суми тільки зі скінчен­ним числом доданків. Для надання змісту виразу в лівій частині останньої рівності розглянемо суму п перших членів:

За формулою суми п перших членів геометричної прогресії
маємо: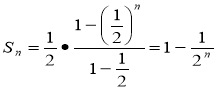 

Якщо п необмежене збільшується (пишуть п →∞), то вираз

 наближається до нуля (пишуть → 0), а вираз 1 -

 наближається до 1.

Отже, S_n =1 —→ 1, якщо  п→∞.

Таким чином, сумою нескінченної спадної геометричної про­гресії називається число, до якого наближається сума п перших членів цієї прогресії, якщо п нескінченно збільшується.

Виведемо формулу суми нескінченної спадної геометричної прогресії

b_l + b_lq +b_l q² +b_lq³ + ..., знаменник якої \q\ < 1.

За формулою суми п перших членів геометричної прогресії маємо:

Якщо \q\ < 1, то при необмеженому збільшенні п вираз qⁿ прямує до нуля, при цьому вираз               теж прямує до нуля.

Отже, S  → при п→∞.

Таким чином, сума S нескінченної спадної геометричної про­гресії дорівнює: S = .

Зокрема, якщо Ь₁  = 1, то маємо S = .

Формули S =,   S =-- справедливі тільки для < 1.

IV. Закріплення нового матеріалу.

Розглянемо приклади.

Задача 1. Знайдіть суму нескінченної спадної геометричної про­гресії 9; 3; 1; ... .

Розв'язання

Оскільки b₁  = 9, q = — , то за формулою S = маємо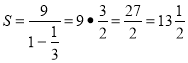
Відповідь. 13

Задача 2. Знайдіть суму нескінченної спадної геометричної прогресії, якщо b₄ = , q = .
Розв'язання: Використовуючи формулу b  при п = 4, знайдемо Ь:

; .

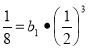Тоді за формулою S = маємо: S =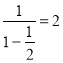 

Колективно розв’язуємо вправ:  544, 546,548

V. Домашнє завдання, підведення підсумків уроку

§ 11,п.11.3, №№ 545, 547,550*

Запитання до класу

1. Яка геометрична прогресія називається нескінченною спадною?

2. Що розуміють під сумою нескінченної спадної геометричної
   прогресії?
3. За якою формулою можна обчислити суму нескінченної спад­ної геометричної прогресії?

Тема: Розв'язування  задач і вправ. Самостійна робота.

Мета: Формування в учнів уміння застосовувати формулу для суми нескінченної спадної геометричної прогресії зі знаменником | q | < 1 до розв'язування вправ, розвивати логічне мислення учнів.

Тип уроку: розв’язування задач і вправ.

Обладнання: картки з завданнями.

Хід уроку.

I.Організаційна частина. ( перевіряю готовність учнів до уроку)

II. Актуалізація опорних знань учнів, перевірка домашнього завдання.

1. Перевірити наявність  виконання домашніх завдань у зошитах

2. Фронтальна бесіда.

Запитання до класу.

• Як слід розуміти запис
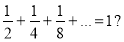
• Яким повинен бути знаменник геометричної прогресії, якщо  відомо, що вона спадна?
• Чому дорівнює сума нескінченної спадної геометричної прогресії?

III. Розв’язування задач і вправ.

1. Вправи № 579, 581, 587
2. Знайдіть суму, доданки якої є членами нескінченої геометричної прогресії (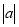<1):

а) 1+; б)

3. Вправа № 276.

IV. Самостійна робота

I варіант

1. Знайдіть суму нескінченної спадної геометричної прогресії:

; ; ; ...;    (3 бали)      

2. Знайдіть суму нескінченної спадної геометричної прогресії, якщо

 b₅ = , q = . (3 бали)

3. Знайдіть суму п’яти перших членів геометричної прогресії, у якої 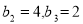. (3 бали)      

4. Знайдіть суму чисел , якщо її доданки є послідовними членами геометричної прогресії.                            (3 бали)      

II варіант

1. Знайдіть суму нескінченної спадної геометричної прогресії:

; ; ;…; (3 бали)      

2. Знайдіть суму нескінченної спадної геометричної прогресії, якщо

 b = , q = . (3 бали)      

3. Знайдіть суму п’яти перших членів геометричної прогресії, у якої .               (3 бали)      

4. Знайдіть суму чисел , якщо її доданки є послідовними членами геометричної прогресії.              (3 бали)      

 

Відповіді: I варіант (1-1; 2- 1,5; 3-15; 4-).

II варіант ( 1- 2; 2-; 3- 40; 4 - ).

V. Домашнє завдання, підведення підсумків уроку 

§ 11, №№ 574, 577, 570, 580*

Тема: Розв'язування  задач і вправ.

Мета: Систематизувати і узагальнити знання, уміння і навички учнів з теми «Числові послідовності», підготуватись до тематичної контрольної роботи; розвинути логічне мислення учнів, пам'ять, уяву, виховати старанність, охайність.

Тип уроку: розв’язування задач і вправ.

Обладнання: таблиця.

Хід уроку

I. Організаційна частина. ( перевіряю готовність учнів до уроку)

II. Перевірка домашнього завдання.

Перевірити наявність виконаних домашніх завдань, перевірити відповіді до завдань.

III. Систематизація та узагальнення знань учнів з теми «Числові

послідовності».

Фронтальна  бесіда з класом за контрольними запитан­нями з використанням табл.1.

Таблиця 1.

Прогресії
	Арифметична	Геометрична
Рекурентна формула	, n є N	, п є N Ь1 0, q 0
Формула п-го члена	an = + (n -1)d
Характеристична властивість	an=
Формула суми п перших членів		, q1 , q=1.
Інші формули
Нескінченна спадна геометрична прогресія ( < 1)

 

IV. Систематизація та узагальнення умінь та навичок учнів з теми «Числові послідовності»

Виконання вправ.

1. Нехай а,  а_п — перший та останній члени арифметичної про­гресії,

d — її різниця, a S_n — сума п перших членів. Заповніть порожні клітинки табл. 2.

Таблиця 2

	a1	d	an	n	Sn
1	1		19	10
2	5	-2		7
3			15	6	60
4	3		-18		-60
5	1	3	28

2. Нехай b₁, b_n — перший та останній члени геометричної про­гресії, q — її знаменник, S_n — сума п перших членів. Заповніть порожні клітинки т. 3.

Таблиця 3

	b1	q	bn	n	Sn
1	1	2		5
2	32	½	2
3		3	81	5
4	6		96	5
5	1	2			15

 

3. Сума трьох чисел, які утворюють арифметичну прогресію, до­рівнює 3О. Якщо від другого числа цієї прогресії відняти число 2, а інші числа залишити без змін, то утвориться геометрич­на прогресія. Знайдіть ці числа.
4. Колективне виконання варіанта 4 із завдань для самостійної
   роботи (с. 252 підручника).

V. Домашнє завдання, підведення підсумків уроку 

Підготуватися до тематичної контрольної роботи. ст..245-247