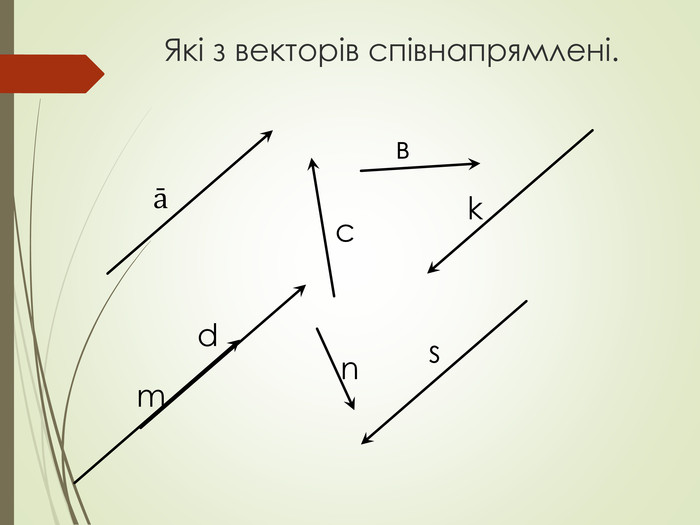
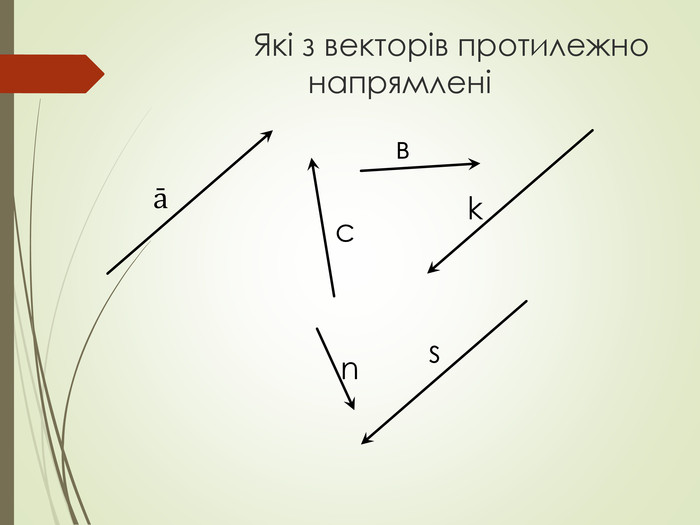
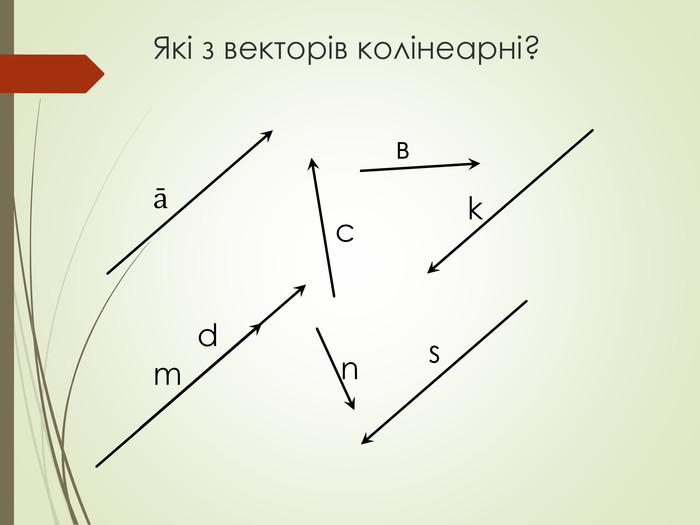
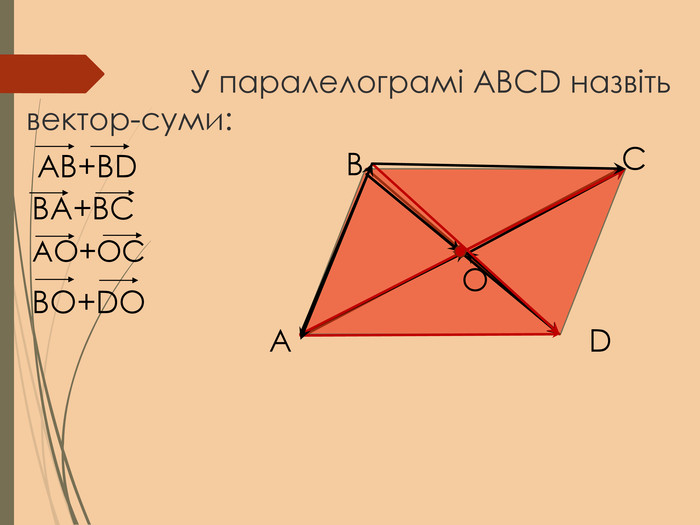
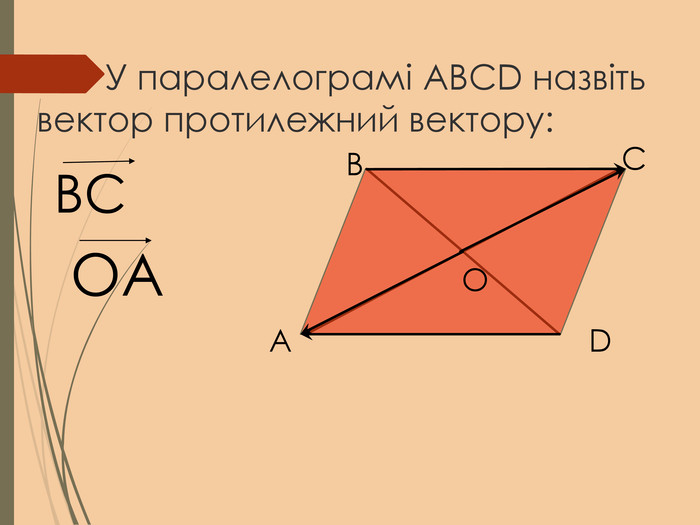
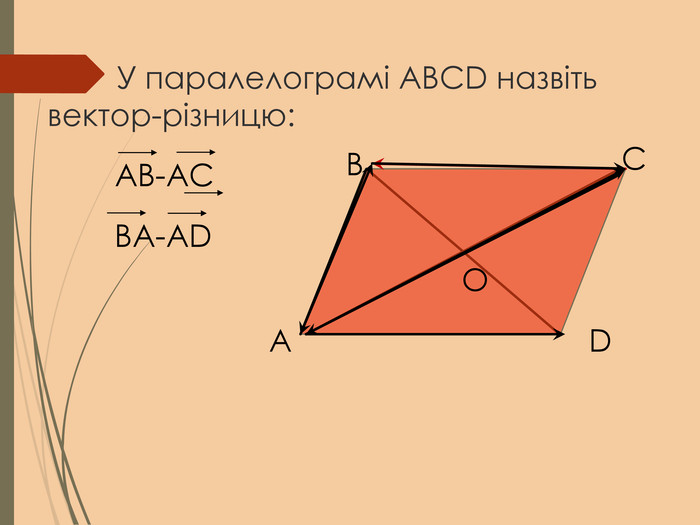
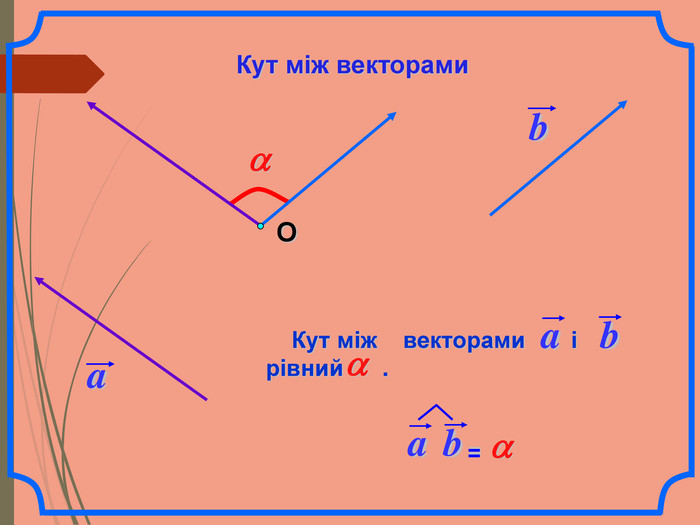
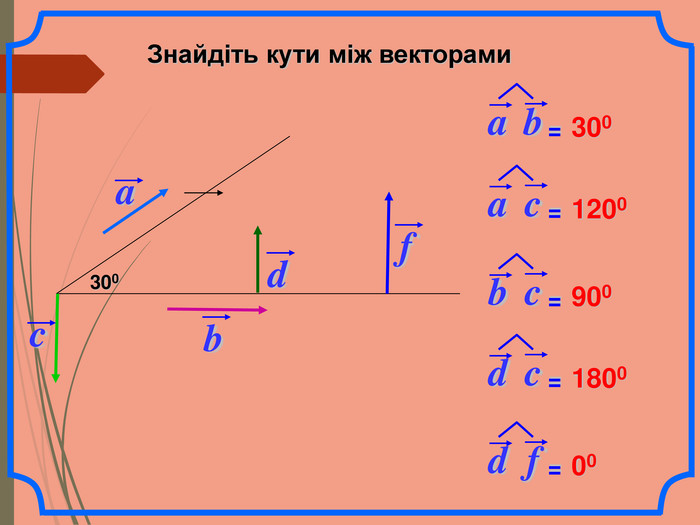
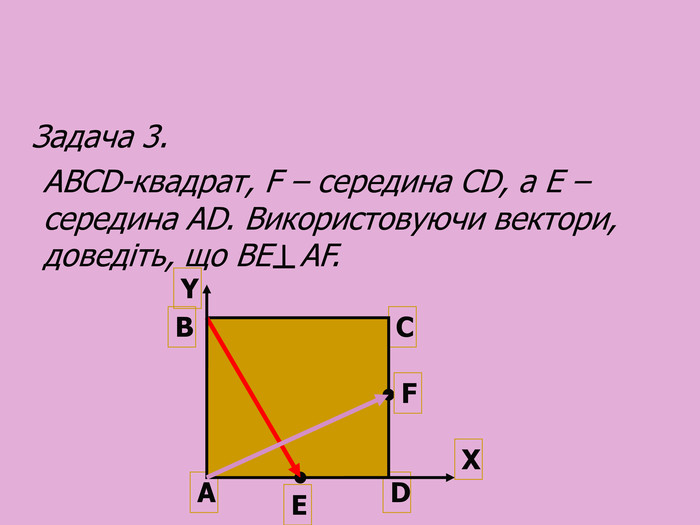
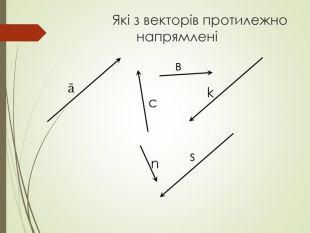
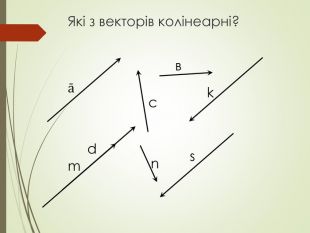
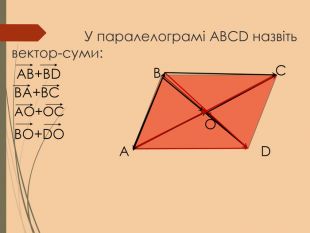
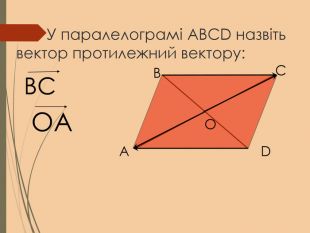
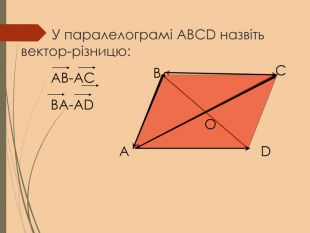
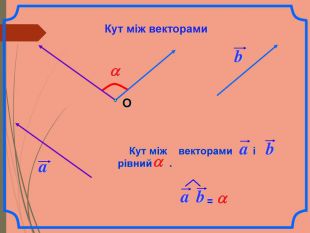
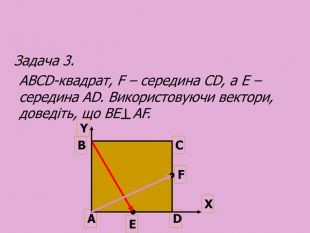
Cкалярний добуток векторів
Про матеріал
Презентацію створено на допомогу вчителеві під час пояснення теми "Скалярний добуток векторів" у темі "Вектори на площині" Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія 9 клас (Єршова А. П., Голобородько В.В., Крижановський О.Ф., Єршов С. В.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку