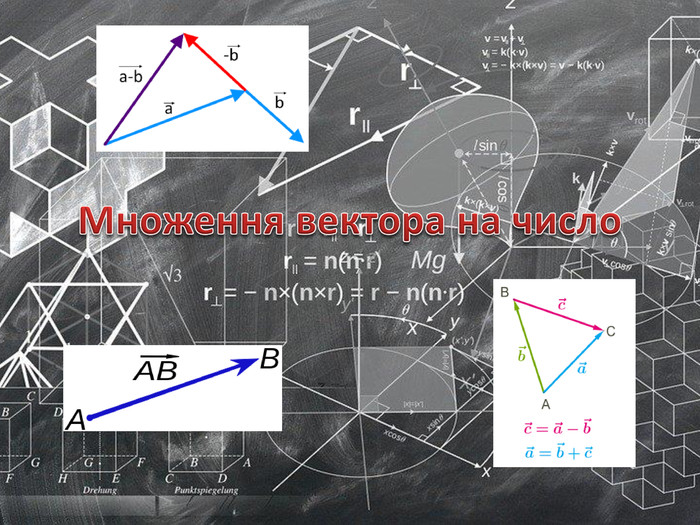
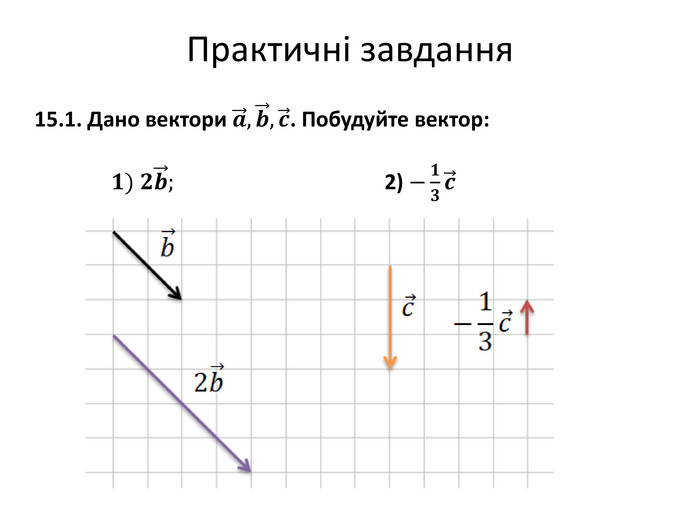
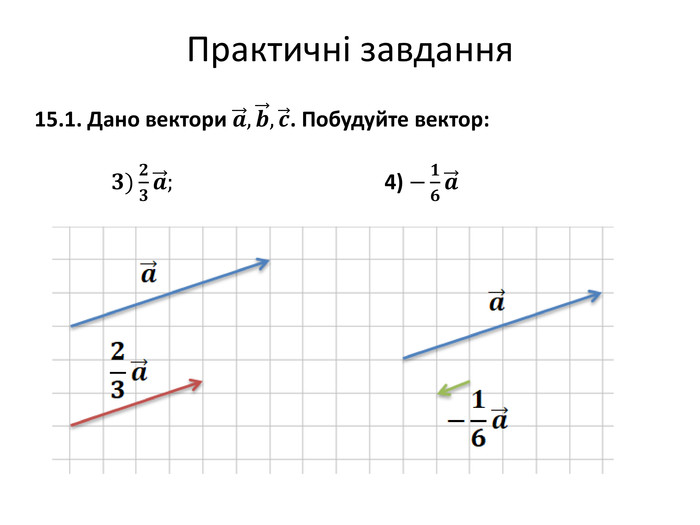
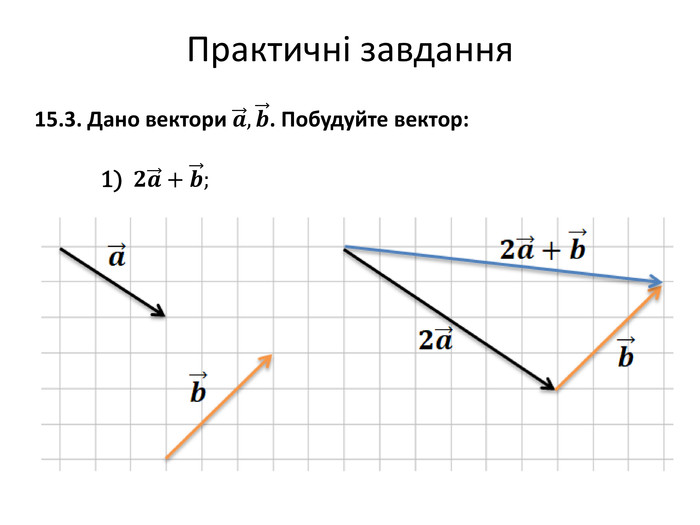
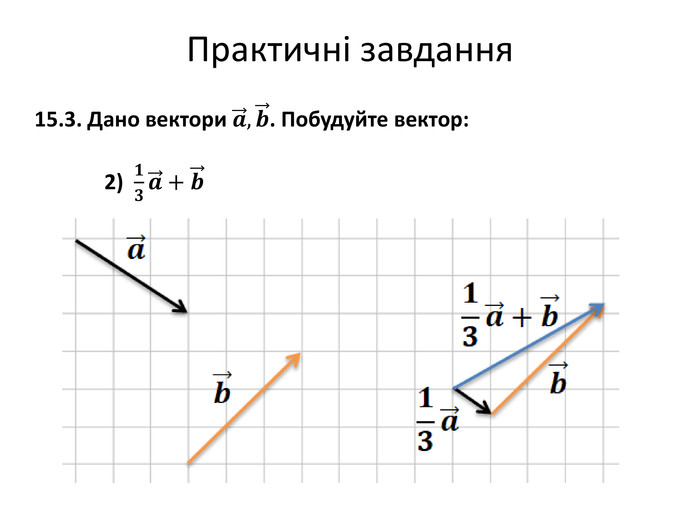
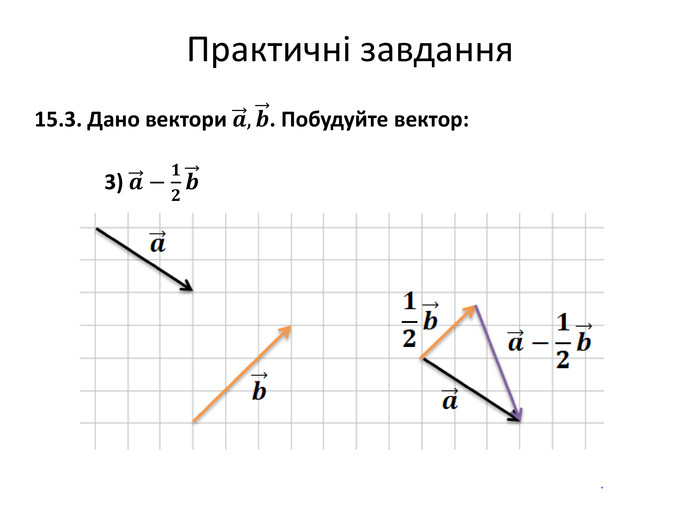
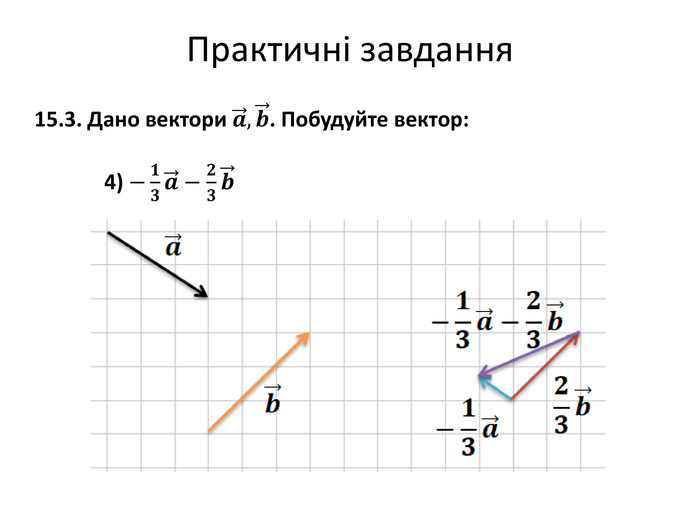
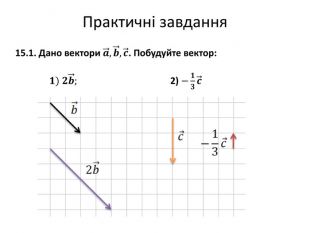
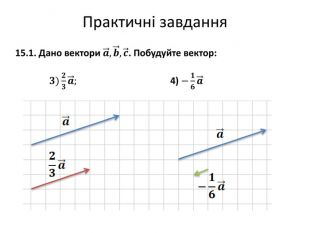
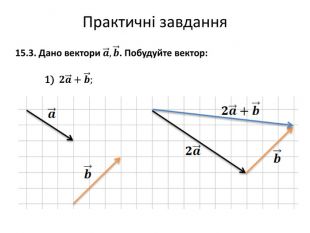
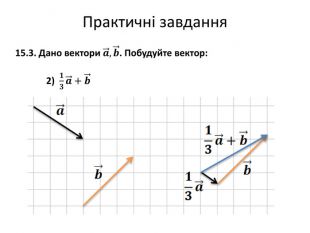
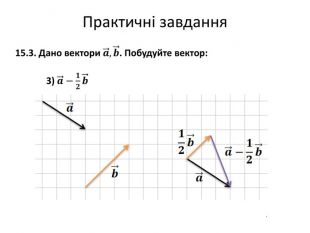
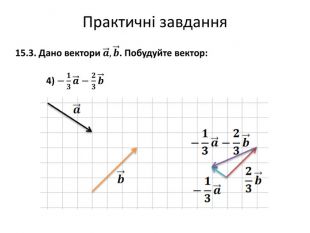
Множення вектора на число
Про матеріал
Презентація може бути використана як допоміжний матеріал до уроку, також при дистанційному навчанні Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Чудовий матеріал!Дякую!
pptx
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку