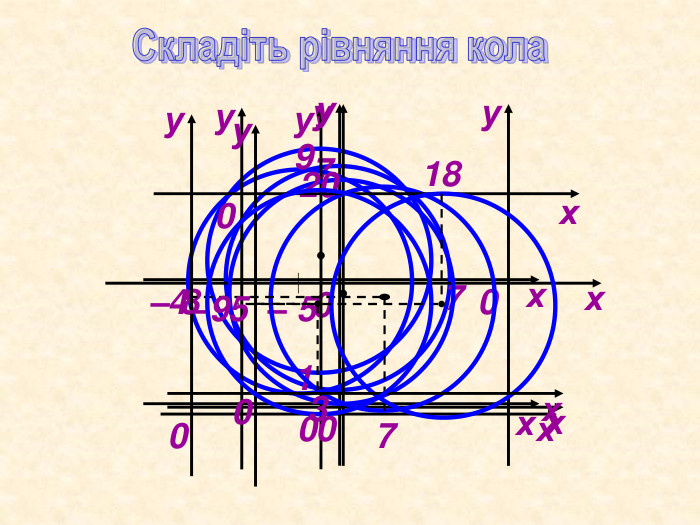
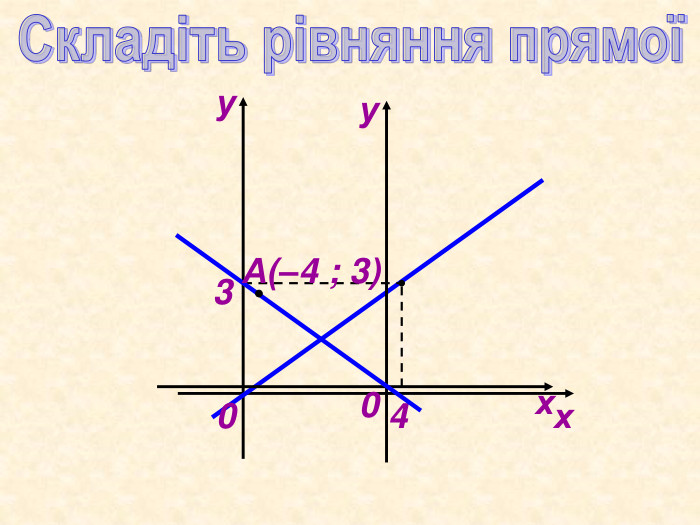
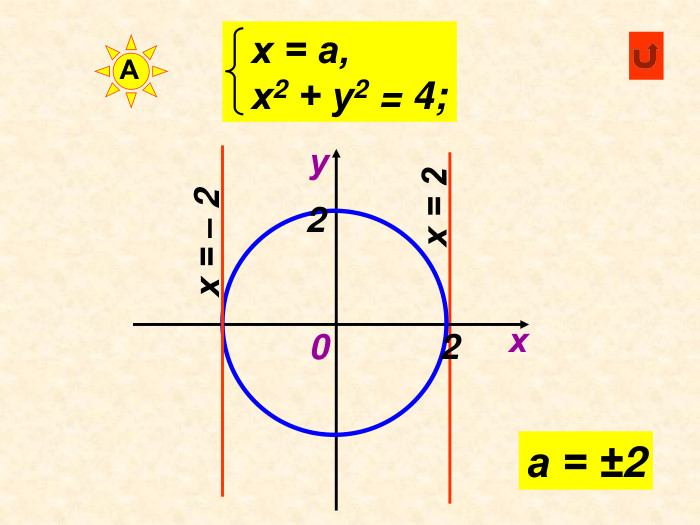
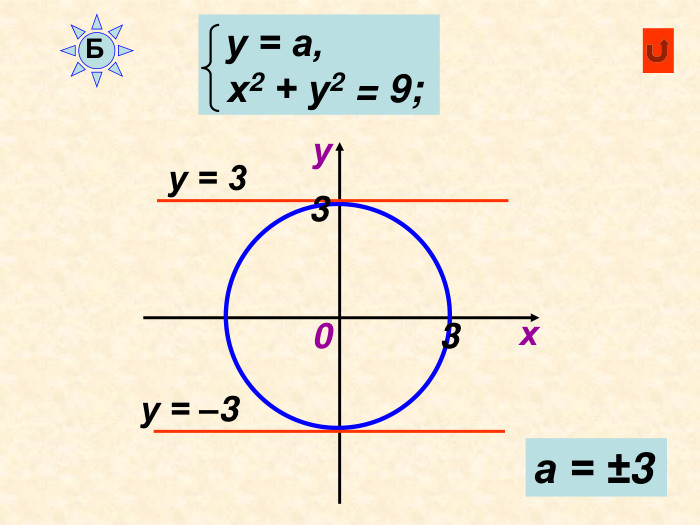
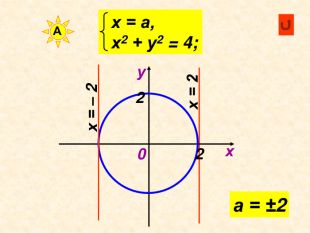
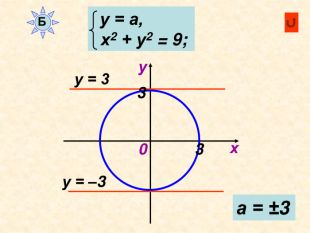
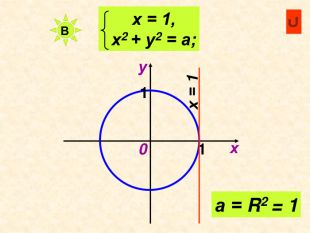
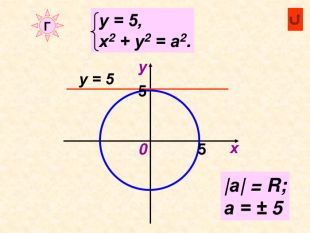
Декартові координати
Про матеріал
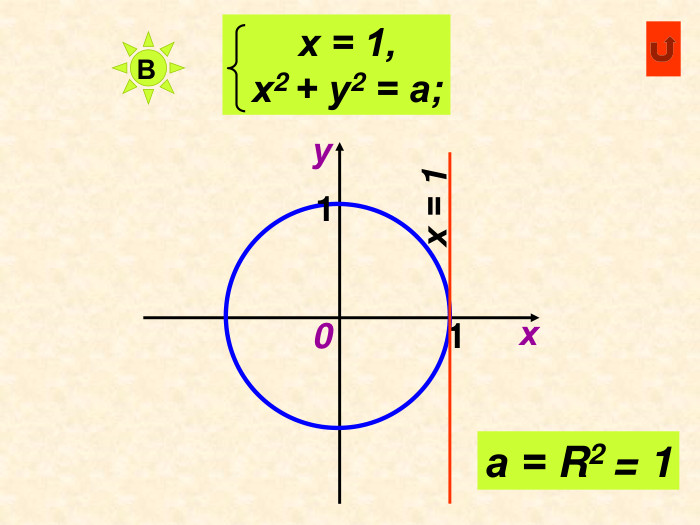
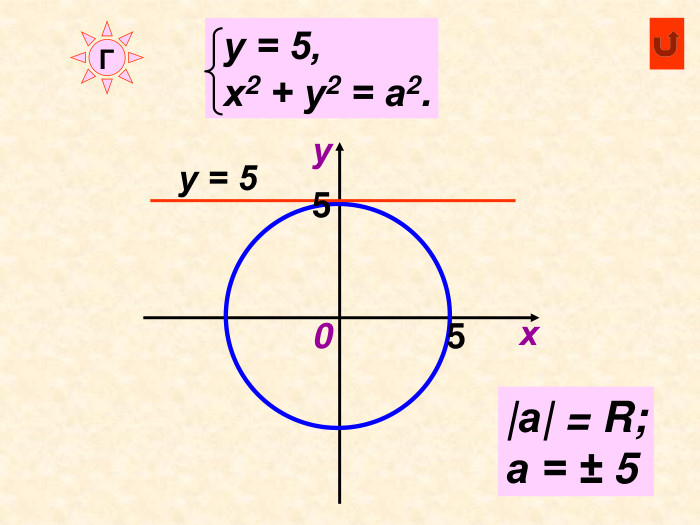
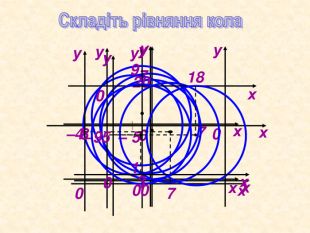
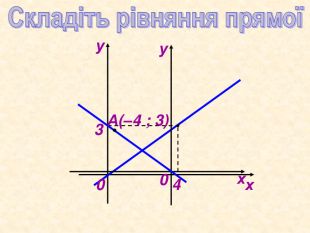
Можна використати як матеріал до уроку або як домашнє завдання при вивченні теми " Декартові координати", завдання використовуються при вивчені рівняння кола та прямої Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку