Дидактичні матеріали для перевірки знань з теми : Криві другого порядку на площині і в просторі

Дидактичні матеріали для перевірки знань з теми :

Криві другого порядку на площині і в просторі.

Варіант № 1.

1. Скласти  рівняння кола з центром в точці (-3;1) і радіусом 5.
2. Знайти точки перетину прямої  х+2у-7=0  і еліпса .
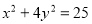3. Задано рівняння гіперболи 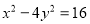. Знайти координати фокусів, рівняння асимптот, ексцентриситет і кут між асимптотами.
4. Скласти рівняння параболи, якщо задані координати фокуса (4;3), а рівняння директриси у+1=0 .
5. Визначити тип поверхні: а) ;

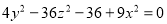                                                 б) .

Варіант № 2.

1. Знайти центр і радіус кола .
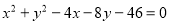2. Скласти рівняння еліпса, якщо задана точка М(2;-2) еліпса і довжина його великої осі = 8.
3. На гіперболі 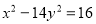взята точка М з ординатою 1. Знайти відстань від точки М до фокусів гіперболи.
4. Скласти рівняння параболи, якщо відомі координати фокуса (7;2) і рівняння директриси  х-5=0 .
5. Визначити тип поверхні: а) ;

                                                 б)

Варіант № 3.

1. Скласти рівняння кола з радіусом 2, що лежить в першому квадранті і дотикаеться осей координат.
2. Скласти рівняння еліпса, якщо задана точка М(-2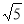;2) еліпса і довжина його малої осі = 6.
3. Знайти ексцентриситет гіперболи,  асимптота якої утворює з дійсною віссю кут 60 градусів.
4. Знайти координати вершин і фокуса параболи 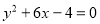. Написати рівняння  директриси і осі симетрії параболи.
5. Визначити тип поверхні: а). ;

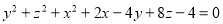                                                 б). .

Варіант № 4.

1. Знайти центр і радіус кола
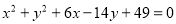
2. Скласти рівняння еліпса, що проходить через точки А(2 3; 6) і В(6;0).
3. Написати рівняння  гіперболи, якщо відстань між фокусами 10, а між вершинами 8.
4. Знайти координати вершини і фокуса параболи 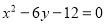. Написати рівняння  директриси і осі симетрії параболи.
5. Визначити тип поверхні: а). ;

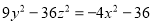                                                 б). .

Варіант № 5.

1. Визначити взаємне розташування кіл: 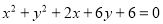і .
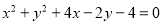2. Скласти рівняння еліпса з ексцентриситетом 0,28 і фокусами(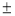7;0).
3. Знайти довжини осей і координати фокусів гіперболи   .         
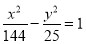4. Знайти точки перетину прямої 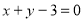і параболи .
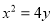5. Визначити тип поверхні: а).;

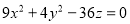                                                 б)..

Варіант № 6.

1. Коло з центром в точці (1;-3) проходить через початок координат. Скласти його рівняння.
2. Через один із фокусів еліпса з довжинами осей 20 і 12 проведена хорда перпендикулярно до великої осі. Знайти довжину хорди.
3. Написати канонічне рівняння гіперболи, якщо довжина дійсної осі 4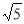, а ексцентриситет .
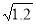4. Скласти рівняння параболи з вершиною в  (0;0), якщо рівняння директриси  2у-7=0 .
5. Визначити тип поверхні: а).;

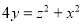                                                 б)..

Варіант № 7.

1. Знайти центр і радіус кола .
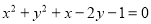2. Еліпс з фокусами на осі ох, симетричними відносно початку координат,  проходить через точку М(2;2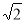). Довжина малої осі 6. Скласти рівняння еліпса.
3. Знайти довжину відрізка прямої 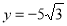, що міститься між вітками  гіперболи                                .
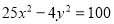4. Визначити координати фокуса і написати рівняння директриси  параболи                                .
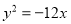
5. Визначити тип поверхні: а).;

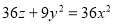                                                 б)..