Тема. Логарифмічні рівняння.

Мета:

Навчальна. сформувати математичні компетенції: поняття логарифмічного рівняння, найпростішого логарифмічного рівняння, здатності до застосування загальних методів розв’язування рівнянь (рівняння-наслідки та рівносильних перетворення рівнянь) та спеціальних методів  розв’язування логарифмічних рівнянь (означення логарифма, потенціювання, заміни, застосування властивостей логарифма, зведення логарифмів до однієї і тієї самої основи, логарифмування),

Виховна.   сприяти формуванню соціальних, полікультурних, комунікаційних   компетентностей, вихованню цілеспрямованості, наполегливості у досягненні поставленої мети, прищеплювати бажання мати якісні, глибокі знання, виховувати культуру математичної мови та мислення, потяг до самовдосконалення, сталий інтерес до вивчення математики

Розвиваюча. Розвивати у студентів пам'ять, логічне мислення, увагу, культуру математичного мовлення, вміння реалізовувати практичні зв’язки курсу математики з фізикою, хімією, біологією. 

Тип уроку:засвоєння нових знань Формування вмінь і навичок.

Хід уроку.

“Не достатньо мати лише добрий розум, Головне-це раціонально застосовувати його” Рене Декарт

І. Організаційна частина. (3-5хв).

ІІ. Актуалізація опорних знань (15   хв).

У вигляді письмової роботи 10 студентів.

Два студенти біля дошки виконують завдання.

Решта  відповідає на запитання

1.      Що називають логарифмом числа?

2.      Які обмеження накладаються на основу?

3.      Яким може бути підлогарифмічний вираз?

4.      Який логарифм називають десятковим і який натуральним?

5.      Яка множина чисел є областю визначення логарифмічної функції?

6.      При якому значенні а функція у= log_a х зростає на всій області визначення?

7.      При якому значенні а функція у= log_a х спадає на всій області визначення?

8.      Що таке логарифмування?

9.      Потенціювання?

ІІІ. Формулювання мети й завдань уроку. Мотивація навчальної

діяльності.

Виступи студентів «Логарифми в різних дисциплінах».

Логарифмічна спіраль

Фізика

Хімія

Бологія

Музика

ІV. Вивчення нового матеріалу

1.         Поняття логарифмічного рівняння.

Рівняння – одна з провідних тем шкільного курсу математики, оскільки розв`язуваня  багатьох практичних задач зводяться до складання й розв`язування рівнянь. Причому багато задач, різноманітних за змістом та з різних галузей діяльності людини, зводяться до рівняння певного виду, яке служить знаковою моделлю цієх групи задач. Уміння розв’язувати певний вид рівнянь дає можливість  розв`язувати цілу групу задач

Логарифмічними рівняннями називають рівняння, які містять змінну під знаком логарифма.

Приклади логарифмічних рівнянь: 

lg х = 1 + lg²x, log₃(x + 3) = 9, lgx = lg x і т. д.

Розв'язати логарифмічне рівняння — це означає знайти всі його корені або довести, що рівняння коренів не має. 

Найпростіше логарифмічне рівняння має вигляд log х = b, де а > 0, а ≠ 1, х > 0. За означенням логарифма випливає, що х = а^b.

Інший вигляд найпростішого логарифмічного рівняння такий:  log_a x = log_a b, де а > 0, а ≠ 1, х > 0, b > 0. 

Із цього рівняння випливає, що х = b. Дійсно із рівності log_a x = log_a b на підставі означення логарифма і основної логарифмічної тотожності маємо: x = a^{loga b} = b.

Найпростішим логарифмічним рівнянням є рівняння log_x a = b, де х > 0, х ≠ 1, а > 0. 

1

За означенням логарифма маємо: х^b = а, звідси х = a^b . 

В основному, всі логарифмічні рівняння, які ми будемо розв'язувати, зводяться до розв'язування найпростіших рівнянь.

Приклад 1. Розв'яжіть рівняння log₃ (2x + 1) = 2.

Розв'язання За означенням логарифма маємо:

2х + 1 = 3², 2х = 8, х = 4. 

Перевірка: log₃(2 · 4 + 1) = log₃9 = 2. 

Відповідь: 4.

Приклад 2. Розв'яжіть рівняння log₃x = log₃(6 – х²).

Розв'язання

Із рівності логарифмів чисел випливає: х = 6 – х²; х² + х – 6 = 0;  х₁ = -3, х₂ = 2.

Перевірка:

1)    Число -3 не є коренем даного рівняння, бо вираз log₃(-3) — не визначений; 

2)    log₃x = log₃2; log₃(6 – х²) = log₃(6 – 2²) = log₃2. Відповідь: 2. 

Приклад 3. Розв'яжіть рівняння log_х+1 (2х² + 1) = 2.

Розв'язання За означенням логарифма маємо: 

2х² + 1 = (х + 1)²; 2х² + 1 = х² + 2х + 1; х² – 2х = 0; х₁ = 0, х₂ = 2.

Перевірка:

1)                      Значення х₁ = 0 не є коренем даного рівняння, оскільки основа логарифма х + 1 не повинна дорівнювати 1.

2)                      log_х+1(2·2² + l) = log₃9 = 2.

Відповідь: 2.

Відзначимо, що в описаних прикладах використовуються тільки такі перетворення, які не приводять до втрати коренів, але можуть привести до одержання сторонніх коренів. Тому перевірка кожного із одержаних коренів обов'язкова, якщо немає впевненості в рівносильності рівнянь. 

2.         Методи розв’язування логарифмічних рівнянь.

Логарифмічні рівняння

1. Метод зведення логарифмічного рівняння до алгебраїчного. Приклад. Розв'яжіть рівняння log²₂ х – 3log₂ x = 4.

Розв'язання

Позначимо log₂ x  через у. Дане рівняння набере вигляду:

у² – 3y = 4;  у² – 3у – 4 = 0;      у₁ = 4; у₂ = -1. Звідси log₂ x = 4,  log₂ x =-1;        x = 2⁴; x = 2^-1;        x = 16,           x =  .

Перевірка:  1) log²₂ 16 – 3 log₂ 16 = 16 – 12 = 4;

² 1

                                     2) log₂    – 3 log₂       =  -1 + 3 = 4. 

2 Відповідь: 16;  .

2. Метод потенціювання.

Приклад. Розв'яжіть рівняння log₅(x – 1) + log₅(x – 2) = log₅(x + 2).

Розв'язання

Пропотенціюємо дану рівність і одержимо:

log₅((x – 1)(х – 2)) = log₅(x + 2);   (х – 1)(х – 2) = х + 2;   x² – 2х – х + 2 = х + 2;  x² – 4х = 0;   х(х – 4) = 0;           х = 0 або х = 4.

Перевірка:

1)    Значення х = 0 не є коренем рівняння, тому що вирази log₅(x – 1) і log₅(x – 2) не мають смислу при х = 0. 

2)    log₅(x–1) + log₅(x–2) = log₅(4–1) + log₅(4–2) = log₅3 + log₅2 = log₅(2·3) = log₅6. log₅(x + 2) = log₅(4 + 2) = log₅6.

Отже, х = 4 — корінь. 

Відповідь: 4.

3.   Метод зведення логарифмів до однієї і тієї ж основи. Приклад. Розв'яжіть рівняння log₃ х – 2logх = 3. 

Розв'язання

                                                    log₃ x – 2logx = 3;       log₃ х – 2 · ^{log3 x} = 3;

                                                                                                                             log₃

log³ x log₃ x – 2·  = 3; log₃ x + 2log₃ x = 3;

1

                                                      3log₃ x = 3;            log₃ x = 1;             x = 3.

Перевірка: log₃ 3 – 2log3 = 1 + 2 = 3. Отже, х = 3 — корінь. 

Відповідь: 3.

4.   Метод логарифмування.

Приклад. Розв'яжіть рівняння х ^lgx = 100х.

Розв'язання

 Прологарифмуємо обидві частини рівності (х > 0), одержимо: lgx ^lgx = lg(100x); lgx lgx = lg 100 + lgx; lg²x – lg x – 2 = 0.

Замінимо lg х = у. Рівняння прийме вигляд: у² – у – 2 = 0; y₁ = 2, y₂ = -1.

Тоді: 1) lg х = 2; х = 10²; х = 100.                 2) lg x = -1; x = 10^-1; x = 0,1.

Перевірка: 1) x^lgx = 100 ^lg100 = 100² ; 100х = 100 · 100 = 100². Отже, x = 100 — корінь.

2) x^lgx = 0,1^lg0,1 = 0,1^-1 =  = 10; 100х = 100 · 0,1 = 10. 

Отже, x = 0,1 — корінь.

Відповідь: 100; 0,1.

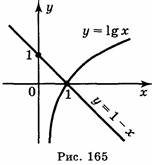
5.   Графічний метод розв'язування логарифмічних рівнянь. Приклад. Розв'яжіть рівняння lg x = 1 – х графічно.

Розв'язання

В одній і тій самій системі координат будуємо графіки функції у = lg x і у = 1 – х (рис. 165). Абсциса точки перетину побудованих графіків дорівнює 1. Отже, х = 1 — корінь даного рівняння. 

3.       Розв’язування логарифмічних рівнянь. log₅²x + log₅ x = 2.

lg(x – 2) -  lg (3x - 6) = lg2

log₄ х  +6 log_х 4  = 5

log₅ хlog₂₅ х log

х ^lgx-1 = 1000

ІV. Підсумок заняття. Оголошення оцінок.

Підведення підсумку у вигляді обговорення переваг кожного методу.

V. Домашнє завдання На окремому аркуші.

ДОДАТОК

З історії логарифмів

Логарифм – з грецької  означає “логос”- відношення і “аритмос”-  число.  

Його винахід пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі». А Бюргі працював разом з астрономом Іоганном Кеплером. Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхів для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, «позбутися нудних і тяжких обчислень, відлякують зазвичай багатьох від вивчення математики». Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів. Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою «Арифметична і геометрична таблиця прогресії». Проте його таблиці не отримали широкого поширення, бо Непер видав свій «Опис дивовижної таблиці логарифмів» на 6 років раніше. Тому і визнали число e неперовим числом.

Понад три з половиною сторіччя з тих пір, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас , продовжуючи життя обчислювачам.

Ще донедавна важко було уявити собі інженера без логарифмічної лінійки в кишені. Винайдена в 1624 році англійським математиком Едмундом Гунтером , вона дозволяла швидко одержувати відповідь з достатньою для інженера точністю до трьох значущих цифр. І хоч тепер її витіснили калькулятори і комп’ютери, проте можна сміливо сказати, що без логарифмічної лінійки не було і перших комп’ютерів.

 Логарифмічна спіраль

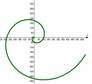Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α.

            Рівняння виражається через логарифмічну функцію.

              Таку криву описує рухома точка, відстань від полюса якої росте в геометричній прогресії, а кут, що описується її радіусом-вектором, - в арифметичній.

Характерні особливості логарифмічної спіралі:                  

ü Має нескінченну кількість витків як при розкручуванні так і при скручуванні;

Її називають рівнокутною спіраллю;

ü В будь-якій точці спіралі кут між дотичною до неї та її радіусвектором зберігає  постійне значення;

ü При різних перетвореннях (гомотетії, повороті) вона залишається незмінною.  

ü Має широке застосування в технічних приладах.

ü Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

Логарифми в фізиці                                

Фізика  завжди вимагає математичних розрахунків, тому знання математики у        фізиці         завжди        необхідне. Ось    декілька      формул,      де використовуються логарифми.

ü Робота, яку виконує газ при ізотермічному процесі

                     A  m RT lnV1  m RT P1

  V₂  P₂ m – маса газу; µ - молярна маса газу; R – універсальна газова стала;

Т  – температура за Кельвіном;

V -  об’єм газу; 

ü     ємність циліндричного конденсатора:           

2 l

C              0 R

                                                   ln(         )

r

L – висота циліндра;

R, r – радіуси внутрішнього та зовнішнього циліндра;  – техн. характеристики конденсатора;

ü     Зв’язок між сталою розпаду, середнім часом життя і періодом піврозпаду Т

                                                     t     ln2

                                     

 T

                               – середній час життя;

                              Т – період піврозпаду;

ü     Рівень інтенсивності звуку

                                         I 

L 10lg I0 

                                      I0 10^12 Вт / м² - умовно нульовий рівень

                         У техніці часто застосовуються ножі, що обертаються. Сила, з якою

вони тиснуть на матеріал, що розрізається, залежить від кута розрізання, тобто кута між лезом ножа і напрямом швидкості обертання. Для того, щоб тиск був сталим, потрібно щоб залишався сталим кут розрізання, а це буде у  тому випадку, коли леза ножів будуть окреслені по дузі логарифмічної спіралі. Завдяки цьому лезо ножа сточується рівномірно.

    Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

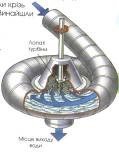У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю.

В астрономії гучність шуму й яскравість зірок оцінюється однаковим чином за логарифмічною шкалою. «Величина» зірки являє собою логарифм її фізичної яскравості. Гучність виражена в белах дорівнює десятковому логарифму відповідної фізичної величини. За логарифмічною спіраллю закручено багато галактик, у тому числі Галактика, яка належить Сонячній системі.

Логарифми в хімії                                  

        Розчини в природі можуть мати різну реакцію середовища: кислу, лужну, нейтральну,що характеризується різною концентрацією йонів Гідрогену С( Н⁺).Для зручності  було введено термін «водневий показник» (рН).

       Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену

рН= - lg С( Н⁺)

            Значення рН може змінюватись від 1 до 14

Показник рН в біологічних розчинах

З таблиці видно, що різні розчини в людському організмі мають різний рН, його відхилення від норми спричиняє захворювання і навіть загибель організму. Людям з підвищеною кислотністю шлункового соку рекомендується пити мінеральну воду  з вищим рН,а зі зниженою кислотністю - "кислішу" воду(з нижчим рН).

Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5. 

У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (рН≈5), а буряк на нейтральних (рН≈7).

Логарифми в біології                                                 

           Можна сказати, що спіраль є математичним символом співвідношення форми і зростання.

 Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння , закручує нитки навколо центра по логарифмічним спіралям.

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується. 

Логарифми в музиці                                                    

Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах.

номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика ( тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса ( тобто дробова частина).