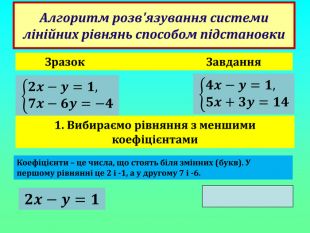
Дистанційний практикум з теми "Розв'язування систем лінійних рівнянь способом підстановки"
Про матеріал
Дистанційний практикум складається з 3 блоків. У кожному з яких пропонується розв’язок зразка і завдання для самостійної роботи учнів за алгоритмом. Можна використати для дистанційного навчання розбивши презентацію на блоки і зберігши кожну частину у pdf файл. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку