Додатні та від’ємні числа. Число 0
6 клас
Тема. Додатні та від’ємні числа. Число нуль
Мета. Сформувати уявлення учнів про зміст поняття «додатні числа», «від’ємні числа», а також виробити вміння відрізняти ці види чисел і виконувати прості вправи, що передбачають таку класифікацію. Розвивати логічне мислення в учнів, виховувати уважність, акуратність.
Хід уроку
- Організаційний момент
Оголошення теми, мети уроку.
- Актуалізація опорних знань
Усні вправи (Мікрофон)
- Обчисліть:
34-23;
45+123;
96+32
125-46
0,23+2,34
6*2,1-3
2,3*5+4
Зобразити на координатному промені точки А(2), В(3,5), С(0), К(5,9), Х(6,5)
За допомогою термометра визначити
а)Яку температуру показує термометр?
Б) Яка температура буде, якщо ртуть підніметься на 3 поділки?
В) -||- -||- на 7 поділок
Г) опуститься на 3 поділки
Д)-||- -||- на 5 поділок
3. Пояснення нового матеріалу
Пояснення проводиться на прикладі термометра
-ввести поняття нуля;
--||- -||- від’ємного числа
-розказати про класифікацію чисел
4. Закріплення знань, формування вмінь
Усні вправи
№№889,890, 892, 893.
Робота із сигнальними картками.
Вчитель називає числа, а учні підносять сигнальні картки, якщо число додатне, то червону картку, а якщо від’ємне, то зелену.
Письмові вправи
№894
А)+150;
Б) -20;
В)-200;
Г)+70;
№ 897

№900

№905
А) 32-23=9
Б) Самостійно 32-41=9
Задача За допомогою таблиці визначити висоту гір, глибину моря
5. Підсумки уроку
З’ясувати , що таке додатні числа , від’ємні числа.
Кожен учень, який сидить на 1-му варіанті назвати додатнє чило, а на 2-му- від’ємне число.
6. Домашнє завдання.
Опрац. П.30, №899,895, 901.
6 клас
Тема: Модуль числа
Мета.Сформувати уявлення учнів про геометричний зміст поняття «модуль числа»; виробити вміння читати, записувати вирази, що містять модуль, а також знаходити значення виразів, що містять числа під
знаком модуля. Розвивати логічне мислення. Виховати культуру запису виразів з модулями, уважність, самостійність.
Хід уроку
1.Організаційний момент.
Оголошення теми, мети.
- Перевірка домашнього завдання.
Наявність домашнього завдання в учнів перевіряють чергові.
- Актуалізація опорних знань.
Задача. Знайти відстань від початку відліку до точок координатної прямої.
А (-4); В (4); С (2); Д (2,5); К (-2).
Запитання класу.
- Чи може відстань бути відємним числом.
- Чи може відстань дорівнювати координаті.
- Чи завжди відстань дорівнює координаті.
- Формування нових знань.
1.Поняття модуля вводимо виходячи з геометричних міркувань, а потім на прикладі з’ясовуємо:
- модуль додатного числа є саме число;
- модуль 0 є 0;
- модуль від’ємного числа є протилежне до даного числа.
- Модуль – це відстань від початку координат до точки А(а).
2. Позначити на координатній прямій точки
![]()
Властивості модуля
1) ![]() = 0
= 0
2) ![]() = а, якщо а >0
= а, якщо а >0
3) ![]() = -а, якщо а < 0.
= -а, якщо а < 0.
- Застосування нових знань, формування вмінь.
Усні вправи. № 943, 945.
Письмові вправи.
№ 946.
![]() = 2.1
= 2.1
![]() = 1.8
= 1.8
![]() = 0.2
= 0.2
![]() = 3.01
= 3.01
![]() = 0.23
= 0.23
№ 948.
а) ![]() =6 г)
=6 г) ![]() = 0 д)
= 0 д) ![]() = 2
= 2
Х = -6 або Х = 6 Х = 0 розв’язку нема
Робота в парах
№ 953.
а) ![]() -
- ![]() = 517 – 311 = 206
= 517 – 311 = 206
г) ![]() :
: ![]() = 7.2:1.8 = 4
= 7.2:1.8 = 4
е) 1.51 + ![]() = 1.51 + 0.372 = 1.882
= 1.51 + 0.372 = 1.882
Самостійно №955.
а) 3.81; -3.01
![]() >
> ![]()
б) ![]() <
< ![]()
№ 959.
Робота в групах
А) ![]() + 53= 73
+ 53= 73
![]() =20
=20
Х = 20 ; Х = -20![]()
![]() +
+ ![]() = 3 в) 4 - 2
= 3 в) 4 - 2![]() = 0.2
= 0.2
![]() = 2
= 2![]() 2
2![]() = 3.8
= 3.8
Х = 2![]() ; Х = -2
; Х = -2![]()
![]()
![]() = 1.9
= 1.9
Х = 1.9; Х = -1.9
№ 961.
а) ![]() < 4 б)
< 4 б) ![]() <
< ![]()
-3, -2, -1, 0, 1, 2, 3
- Підведення підсумків уроку.
З’ясувати чи може бути рівність ![]() = -2.
= -2.
- Домашнє завдання
№ 954 (а-г), 960 (а,в), 962 (а).
6 клас
Тема: Розв’язування задач і вправ.
Мета. Вдосконалення вміння учнів розв’язувати вправи на порівняння раціональних чисел. Розвивати логічне мислення. Виховувати
акуратність.
- Організаційний момент.
Оголошення теми, мети.
- Перевірка домашнього завдання.
Учні зачитують домашні вправи і коментують.
На дошці записано вирази, один учень під час перевірки домашнього завдання виконує, а інший потім перевіряє.
Завдання.
Порівняйте числа.
12,3 і 5,9
24,6 і -13,67
35,42 і –26,25
-23 і ![]()
![]()
- Розв’язування вправ.
№ 991.
а) -5<0 б) 7> 0
в) Х < 0 г) в > 0
№ 992.
-0,02; 3,2; -4,3 -1,9; 0,5; -![]() .
.
-4,3 ; -1,9; -![]() ; -0,02; 0,5 ; 3,2.
; -0,02; 0,5 ; 3,2.
№ 993.
а) -1, 0, 1, 2.
б) 0, 1, 2, 3.
в) -39, -38, -37
№ 997.
60.
№998.
![]() < 24
< 24
A<24
-а < 24
a>- 24
-23 – найменше; -1 – найбільше.
№ 1000.
а) Так
б) Ні
Робота в парах
№ 1001.
a > b правильно
a<b неправильно
Перша пара, яка виконала завдання коментує його.
№ 1004.
А) 3.
Б) 4).
В) 1).
Г) 2.
- Підведення підсумків уроку.
Відповіді на запитання учнів
Повторення правила порівняння раціональних чисел.
- Домашнє завдання №989, 994, 996.
7 клас
Тема: Сума кутів трикутника. Зовнішній кут трикутника і його властивість
Мета. Домогтися засвоєння учнями змісту теореми про сум кутів трикутника та змісту її доведення, а також деяких висновків з цієї теореми. Вироблення в учнів вміння застосовувати зміст теореми і висновків з неї, а також використання сформульованих тверджень при розв’язуванні задач на знаходження градусних мір кутів трикутника. Формувати уявлення учнів про зовнішній кут трикутника, його властивості. Формувати вміння учнів розв’язувати задачі на використання даних властивостей. Розвивати геометричну уяву учнів. Виховувати самостійність, уважність, акуратність і точність при побудові геометричних рисунків.
Хід уроку
- Організаційний момент.
Оголошення теми, мети.
- Перевірка домашнього завдання.
Перевірку домашнього завдання провести у вигляді математичного диктанту.
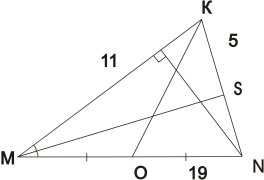
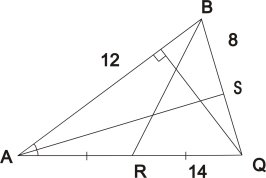
1. Назвати:
а) вершини трикутника
б) сторони трикутника
в) бісектрису трикутника
г) висоту
д) медіану
с) периметр трикутника.
2. Сформулювати означення
а) трикутник – це а) бісектриса – це
б) медіана – це б) висота – це
в) рівнобедрений трикутник – це в) рівносторонній трикутник - це
- Формулювання мети і завдання уроку. Мотивація навчальної Давайте побудуємо трикутник, у якого всі кути тупі або прямі. Отже, побудувати не можна, а це спонукає до думки, що сума кутів трикутника є певне число, яке дорівнює 1800.
Формулюю тему, мету уроку.
- Актуалізація опорних знань.
Чи є на рисунку пари суміжних кутів.
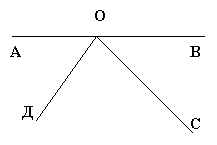

- Засвоєння нових знань.
- Теорема про суму сторін в трикутнику та її доведення.
Сума кутів в трикутнику дорівнює 180°.
Дано ΔАВС . Доведемо, що ![]() A+
A+![]() B+
B+![]() C=180°
C=180°
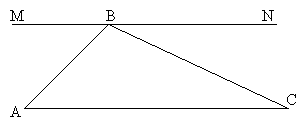
![]() C=
C=![]()
![]() А=
А=![]()
![]() +
+![]() В+
В+![]() =
=![]() +
+![]() В+
В+![]() =1800.
=1800.
2.Наслідки з теорем.
З’ясувати з учнями наслідки з теорем.
Наслідок1. Трикутник може мати лише 1 прямий кут або тупий, тоді два інші кути гострі.
Наслідок2. Сума гострих кутів прямокутного трикутника дорівнює 900.
- Зовнішній кут трикутника.
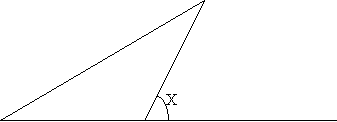
Теорема (Властивість зовнішнього кута трикутника).Зовнішній кут трикутника дорівнює сумі двох кутів трикутника не суміжних з ним.
Наслідок. Зовнішній кут трикутника більший за кожен кут не суміжний з ним.
6.Формування вмінь розв’язувати задачі.
Усно №6, 8.
Письмово №13(1), 15(1), 18(1)
- Підведення підсумків уроку.
Повторити вивчені на уроці теореми.
- Домашнє завдання.
Опрацювати §11. №12, 18(1).
6 клас
Тема. Розв’язування вправ..
Мета. Завершити роботу з відпрацювання навичок множення та ділення раціональних чисел, використання властивостец множення раціональних чисел для розкриття дужок, зведення подібних доданків. Розвивати позитивні риси особистості; виховувати почуття патріотизму, відповідальності за доручену справу, здійснювати міжпредметні зв’язки з історією..
Обладнання: сигнальні картки, картки-завдання; підручник для 6-го класу.
Тип уроку: комбінований.
Хід уроку
Розум полягає не лише в знаннях, але
й у вмінні застосовувати ці знання.
Арістотель
І. Організаційний момент
Учитель.
Урок цікаво, щоб почати,
Загадку дам вам відгадати:
Наук цариця недосяжна,
Могутня, щедра і прекрасна,
Блискуче розум розвиває,
Правильно мислити навчає.
Неперевершена її краса,
Чудова логіка струнка.
Ну, діти, хто вона така?
…………
Ми з вами на уроці математики.
Повідомлення теми, очікуваних результатів
Продовжуючи вивчати тему «Множення та ділення раціональних чисел», проведемо цей урок у формі подорожі. На нас чекають цікаві зупинки. Хочу зауважити, що в роботі нам допоможе вислів давньогрецького філософа і вченого Аристотеля «Розум полягає не лише в знаннях, але й у вмінні застосовувати ці знання». Вам надається можливість застосувати свої знання і вміння.
Ми здійснимо подорож на козацькій чайці за маршрутом: Дніпро, Чорне море, Босфорська протока, потім – Середземне море, Гібралтарська протока, а далі, перетнувши Атлантику, дійдемо до берегів Північної Америки.
Образ запорізького козака став символом захисника Батьківщини. Козацтво захищало українські землі від руйнівних набігів турецько-татарських загарбників, повернуло до життя спустошені татарськими ордами південноукраїнські землі. Запорізькі козаки піднялися у військовій справі до рівня кращих європейських армій XVII-XVIII ст.
Досконало володіли мистецтвом морського бою. Їхній флот складався із чайок – легких маневрених човнів, які мали два керма (кормове і носове), рухалися як на веслах, так і з допомогою вітрила. Чайки вміщували 50-70 козаків, озброєних рушницями і шаблями та невеликими гарматами
Саме в козаках український народ бачив своїх найбільш надійних захисників. От що писав мандрівний поет XVII сторіччя Климентій Зинов’єв:
...Козаків, немов святих, треба шанувати.
Позаяк і кров свою в битвах проливають.
Тим з небес подай свою, Господи, корону,
Хто для нашої землі лагодить оборону.
ІІ. Актуалізація опорних знань
І етап «Старт»
- На цьому етапі потрібно привести екіпіровку чайки в повний порядок: розкласти все по своїх місцях, щоб нічого не заважало в подорожі. Для цього у вас на столах лежать картки , я прошу їх перевернути і ми з вами пограємо гру мікрофон.
- -2∙ 52
- 3 ∙ 12
- -6 ∙ 12
- -50: 2
- -4 ∙ 0 ∙ 6,2
- 45 ∙ 2
- -45:(-5)
- -13 ∙ (-2)
- 24:(-12)
10) -5 ∙ (-20)
11) 2∙ ( - 15)
12) 6∙ 0 ∙ (-3)
13) -1 ∙ 5,2
14) -36:(-2)
15) -28:(-7)
16) -64:8
17) 75:(-15)
18) -80:(-4)
ІІІ. Відпрацювання навичок
ІІ етап «Маршрут руху»
Ми успішно подолали першу частину шляху – Дніпро і вийшли у Чорне море. Ми правильно склали маршрут, рухались правильним курсом, але шторм збив нас з курсу. Щоб зорієнтуватися в просторі, нам треба розв’язати завдання, за правильними відповідями відшукати слово, яке вкаже на курс нашої подорожі.
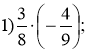
 3)
3) 
4) ![]() 5)
5) ![]() 6)
6) ![]() .
.
|
Б |
А |
О |
Р |
Д |
М |
Ф |
О |
С |
У |
К |
|
|
|
2 |
6 |
– 2 |
– 9 |
– 3 |
3 |
– 6 |
8 |
12 |
Ми правильно відгадали: наш курс – Босфор.
Історикознавець. Босфор – протока між Європою та Малою Азією, з'єднуюча Чорне море з Мармуровим і разом з Дарданелами – з Середземним. За легендою свою назву протока отримала завдяки Іо. Щоб уникнути гніву своєї дружини Гери, Зевс перетворив свою прекрасну кохану на ім’я Іо у білу корову. Нещасна Іо обрала водний шлях порятунку, пірнувши у синій вир протоки, що з тих пір так і називається «коров'ячим бродом» або Босфором. З обох боків протоки розташоване історичне місто Константинополь, сьогоднішній Стамбул. Стамбул розташований одразу в двох частинах світу — Європі та Азії — і немов з’єднує їх у вічному поцілунку. Багаторазово змінював своє ім’я, кожне з яких знаменує яскраві періоди світової історії, – Візантія, Новий Рим, Константинополь, Стамбул, Царгород.
ІІІ етап «Поповнення запасів їжі і питної води»
Робота з сигнальними картками:



Тестові завдання (учні підіймають картку з правильною, на їх думку, відповіддю).
Обчислити:
![]()
А: 36 Б: – 36 В: 14
![]()
А: 48 Б: – 48 В: – 16
![]()
А: 8,7 Б: – 8,7 В: 0
(–1)2
А: – 100 Б: – 1 В: 1
(–1)3
А: 1 Б: – 1 В: – 121
![]()
А: –40 Б: 48 В: -48
ІV етап «Пірати»
І знову ми в дорозі. Ми пливемо Середземним морем. Що ж це? На нас накинулися пірати. Щоб врятуватися від піратів, вам необхідно розв’язати вправи
Спростити вирази
- 4(х+7) +5(x-3)
- 2(x-4)-2(x+3)
Винести за дужки спільний множник
- 8xy+16xz+24ax
- 25ab+15ac-30ak
V етап «Гібралтар»
Історикознавець. Гібралтар, територія на півдні Піренейського півострова, біля Гібралтарської протоки включає в себе скелястий півострів (висотою до 425м.) і піщаний перешийок, що з'єднує скелю з Піренейським півостровом. Гібралтар був відомий ще стародавнім грекам і римлянам під назвою Кальпе. У 8 ст. перетворений арабами у фортецю, що була названа Джебель-ат-Тарік (гора Таріка) на честь арабського завойовника Таріка ібн Сеїда. Пізніше ця назва була перекручена, і фортеця стала називатися Гібралтар.
Щоб пропливти протоку, треба пройти випробування.
Троє учнів виконують завдання на картках-корабликах на дошці, а решта в зошитах.
5(x+3)+4=10
2(x-3)+7=11
2x+3(x+1)=15
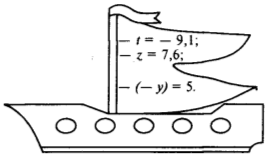
І ось, нарешті на горизонті з’явився маяк, вогник якого ледь-ледь світить у далечині.
Робота в парах.
1) ![]() 2)
2) ![]()
![]()
![]()
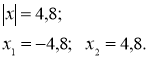
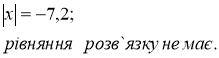
ІV. Підсумки уроку та пояснення домашнього завдання.
Ось і закінчилася наша подорож. І закінчувати урок вже настала пора, але щоб його закінчити потрібно дати відповіді на запитання.
- Як знайти добуток двох чисел з різними знаками?
- Як знайти добуток двох від’ємних чисел?
- Сформулювати сполучну властивість множення.
- Сформулювати переставну властивість множення.
- Які доданки називають подібними?
- Сформулювати розподільну властивість множення.
Сьогодні ви не витрачали час, тому є кандидати для нагород у нас(Оцінювання учнів).
V. Домашнє завдання №1191,1199.
6клас
Тема: Розв’язування задач і вправ.
Мета: відпрацьовувати навички застосування означення модуля для обчислень виразів і розв’язування рівнянь з модулями. Розвивати навички усної лічби, виховувати уважне, ввічливе ставлення один до одного, виховувати любов до природи.
Тип уроку. Урок систематизації знань і вмінь.
Хід уроку.
І. Організаційна робота до уроку. Оголошення теми, мети уроку
Учитель читає текст казку. Учні виконують поставлені завдання
ІІ Перевірка домашнього завдання . Учень зачитує домашню вправу №954.
Фронтальне опитування.
1.Які ви вже знаєте числа.
2. Які числа називаються додатніми, відємними.
3. Які числа називаються протилежними.
4. Що таке модуль числа.?
ІII. Розв’язування вправ.
Жили собі сестричка та братик. Сестричку звали Олеся, а братик – Василько. От якось і каже Олеся:
- Василю, чуєш Василю, давай гратися в піжмурки.
- Добре, відповідає Василько, - давай.
І почали вони гратися. Тільки як братик заховається, то Олеся бігає, шукає, а знайти Василька не може. Стало їй дуже прикро від цього, тому вона сіла й гірко заплакала. Плаче й плаче, аж чує, хтось говорить до неї:
- Чого ти плачеш, дівчинко?
- Як же мені не плакати? – відповідає крізь сльози Олеся. – Як я заховаюся, то Василько мене одразу знайде, а як Василько заховається, то я шукаю, шукаю, а знайти не можу.
_ Ну, добре, - каже той же голос. – Я тобі допоможу так заховатися, що Василько тебе не знайде, але ти повинна позначити на координатній прямій числа
Допоможемо Олесі виконати завдання незнайомця? Позначимо на координатній прямій точки (Два учні позначають точки)
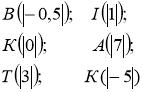
Якщо прочитати слово,що утворилось, то дізнаємося, де заховалася Олеся. (Квітка)
Гарно Олесі у квітці, затишно, спокійно. Як гляне через пелюсточки, то все навколо таке, наче дивиться вона на світ крізь кольорове скельце. А на пелюстках квітки написані математичні приклади. Спробуємо розв’язати їх. Та назвати які ці числа. ( Учні відривають пелюстки квітки і розв’зують приклади, записані на них.)
Завдання на пелюстках:
1. ![]()
2. ![]() ;
;
3. ![]()
4. ![]()
5. ![]()
Навчилася Олеся й такі приклади розв’язувати.
- Еге, думає та тут таки гарно! Хай Василько скрізь побігає, зазирає за кожен кущ, за кожен горбочок. А мене не знайде, хоч плач!
Щоб знайти Олесю, Василькові спочатку потрібно для значення х=2 виконати ланцюжок обчислень результат якого дорівнює висоті горбика в метрах , на якому є квітка, де сховалась Олеся.
Х = 2

![]()
![]()
![]()
![]()
![]()
![]()
Олеся сидить у квітці, сміється.Аж чує, що до квітки хтось летить та гуде, як літак, ще й дзижчить! Підлетіло до квітки, сіло на край пелюстки, а потім швидко до серединки! Злякалась Олеся, як замахає руками, закричить:
- Ой буюся, боюся!
Спинилось воно, побачило дівчинку у квітці і каже: «Ти не кричи і не бійся мене.
- Я – бджілка, - промовила незнайомка, - хоч і волохатенька, але золотиста, чепурненька.Випускаю свій носик, встромлюю його в денце квітки і починаю смоктати чистий пречистий нектар, прозорий як сльоза.
- Мені теж нектару хочеться. – попросила Олеся.
- То летімо разом. Але, щоб потрапити до мого житла, потрібно розв’язати кілька рівнянь і найбільший розв’язок вкаже скільки метрів до вулика:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Тож скільки метрів, діти до вулика? Щойно долетіла Олеся з бджілкою до вулика, запахло медом. А скільки його – полічимо, розв’язавши задачу: В одному вулику було ![]() кг меду, а в другому у 2 рази більше. Скільки меду в обох вуликах.
кг меду, а в другому у 2 рази більше. Скільки меду в обох вуликах.
![]() (кг)
(кг)
![]() (кг)
(кг)
Посадила бджілка Олесю за стіл, принесла цілу миску меду. Коли Олеся наїлася меду, то враз згадала про Василька.
- Ой лишенько! Та це ж він, бідолашний, бігає скрізь та шукає мене!
Шкода їй стало брата, але, щоб вийти з вулика, слід знайти код, який дорівнює значенню виразу ![]() , якщо
, якщо ![]() =6.
=6. ![]() =-0,2
=-0,2
Допоможіть Олесі обчислити вираз і якнайшвидше вийти з вулика.
Олеся швиденько знайшла та як закричить з усієї сили: « Василю, Я осьдечки!»
І прокинулась. Бо все це їй наснилося: і про квітку, і про бджілку, і про мед.
Дружіть з природою, оберігайте рослини, піклуйтесь про тварин, і вам насняться гарні солодкі сни.
ІV. Підсумок уроку
Найактивнішим учням виставляються оцінки, Учитель проводить підсумок уроку, виставляє оцінки, зосереджує увагу учнів на помилках, які вони допускали під час виконання вправ та обчислень.
Отже, діти..........
Найдавніша на планеті,
Між наук цариця,-
Математика – ти наша
Вірна помічниця.
Чи будинок зводиш, друже,
Чи пливеш морями –
Скрізь вона тобі послужить,
Всюди вона з нами.
V. Домашнє завдання. №№955, 956, 957 .
6 клас
Тема. Розв’язування вправ.
Мета: відпрацювати навички використання ознак подільності для виконання завдань, шо передбачають означення подільності чисел. Виховувати уважність, спостережливість. Розвивати логічне мислення, навики усної лічби.
Хід уроку
І. Перевірка домашнього завдання
1. З’ясувати , які з чисел діляться на 2, 5, 10:
425; 524; 522; 225; 2 250; 5 100.
II. Актуалізація опорних знань
Усні вправи
1. Обчисліть: а) 55 + 125; 37 + 16; 82 - 41; 65 - 17;
б) 5,3 + 7; 0,2 + 3,5; 4 - 3,8; 6,7 - 5; в) 12∙5; 1,3 ∙ 3; 4,6 : 2; 3 : 0,3.
Серед натуральних чисел знайти число яке ділиться і на 2 і на 5 і на 3 одночасно.
Серед чисел знайдіть те, що задовольняє найбільшу кількість ознак
подільності: 12; 15; 45; 450.
III. Відпрацювання навичок
Передбачається, що на цьому уроці учні виконують завдання достатнього і середнього рівнів складності, бо ознаки подільності засвоєні.
ІІ, III рівні
Письмові вправи
Напишіть п'ять найбільших трицифрових чисел, які діляться на 10.
Знайдіть суму всіх двоцифрових чисел, які діляться на 10.
Напишіть п'ять найменших натуральних чисел, які діляться на 5;
5 найменших трицифрових чисел, які діляться на 5.
Знайдіть суму всіх непарних одноцифрових чисел.
Допишіть до числа 327 справа таку цифру, щоб утворене чотирициф
рове число ділилось на 2 і на 5. Чи ділиться воно на 10?
Допишіть до числа 11 справа таку цифру, щоб утворене трицифрове
число ділилось на 3? на 9? Чи буде воно парним?
Число а ділиться на 9. Чи ділиться воно на 3? Число я ділиться на 3. Чи
ділиться воно на 9?
Додаткові вправи
Напишіть найбільше трицифрове число, яке ділиться на:
а) 2 і 3; б) на 2 і 9; в) на 2; 3 і 5.
Знайдіть двоцифрове число, яке одночасно кратне 2, 5 та 7.
Виразіть у тоннах: 134 кг; 1248 кг; 9 ц; 54 211 кг.
Мідна руда місить 8 % міді. Скільки міді міститься у 260 т такої руди?
IV. Підсумок уроку
Бліцконтроль. З'ясуйте, чи правильні твердження: 15 240 ділиться: 1) на 2; 2) на 9; 3) на 10; 4) на 5; 5) на 45; 6) є простим числом?
V. Домашнє завдання №43, 47,51.
7 клас
Тема. Розв’язування рівнянь. Властивості рівнянь
Мета: повторити та узагальнити знання учнів про зміст поняття
«рівняння» та пов'язаних з ним понять і способи розв'язання рівнянь
що відомі учням з початкової школи та 5,6 класуів; сформувати уявлення
про основні види рівносильних перетворень лінійних рівнянь з однією
змінною (на інтуїтивному рівні); розпочати роботу з вироблення вмінь
виконувати основні рівносильні перетворення рівнянь для їх розв’я
зування.Розвивати навики усної лічби. Виховувати уважність, спостережливість.
Хід уроку
1 Організаційний момент
Оголошення теми, мети уроку
2. Актуалізація опорних знань
Усні вправи
1. Обчисліть:
-2,8-3,2 1,4-8,2 0,8-7 -10+1,8
:1,2 :3,4 -1,9 :0,41
а) 1,6; б) -0,5; в) :3; г) +5,4.
+8,5 +0,8 -0,2 0,5
? ? ? ?
2. Використовуючи правила знаходження невідомих компонентів арифметичних дій, розв'яжіть рівняння (знайдіть корінь рівняння)
а)х-2,2=-0,8; б)х+2,2=-0,8; в)х-(-2,2)=-0,8;
г)х:(-2,2)=-0,8; д)-2,2:х=-0,8; є)-2,2-х=-0,8; ж)(х-З)(х-2)=0.
3. Спростіть вираз: а) 5а-7а+8b- 2b; 6)3x-4y-x-y>; в)х-(2х-1); г)-(х+1)+(х-1), д)-2(а-3), г)-0,2(-2а+0,3).
3. Мотивація навчальної діяльності
Задача. На одній шальці терезів лежать два однакових бруски мила, на іншій один такий брусок та ще гирка масою 100 г. Скільки важить один брусок мила?
Розв'язання. Зрозуміло, що один брусок важить 100 г. Але якщо записати рівняння, що відповідає умові задачі, прийнявши масу бруска мила за х (г), будемо мати: 2х= х+100 — бачимо, що невідоме знаходиться в різних частинах рівняння. Такі рівняння ми поки що розв'язувати не вміємо. Отже, треба дізнатись про певну властивість, яка допоможе нам розв'язати рівняння, що мають невідомі в різних частинах рівняння (вчитель повідомляє тему уроку).
4. Повторення та систематизація знань
Перш ніж розібрати з учнями основні види рівносильних перетворень рівнянь, бажано повторити та систематизувати знання про рівняння, які учні повинні мати на цей час, а саме:
зміст поняття «рівняння» (рівність, в якій є невідоме число);
корінь рівняння (значення змінної, яке перетворює рівняння на
правильну рівність);
що означає «розв'язати рівняння» (знайти всі корені або довести, що
їх немає);
які правила ми використовували до цього моменту під час розв'язування рівнянь (залежності між-компонентами арифметичних дій та
властивість нуля при множенні).
5. Формування знань
Після проведеного повторення та систематизації знань учнів ми на інтуїтивному рівні формуємо уявлення про основні види рівносильних перетворень рівнянь. Формувати такі уявлення можна за допомогою використання наочно-предметних засобів, зокрема уявлення про терези, що в рівновазі (якщо на обидві шальки терезів, що перебувають у рівновазі, покласти гирки однакової маси або з обох шальок таких терезів прибрати гирки однакової маси, то терези залишаться в рівновазі).
Таким чином формуємо уявлення про першу властивість рівнянь: Корені рівняння не зміняться, якщо будь-який доданок (доданки) перенести з однієї частини рівняння в іншу, змінивши при цьому його знак (на протилежний).
6. Закріплення знань. Вироблення вмінь
Усні вправи
1. Чи правильно виконано перенесення доданків з однієї частини в іншу
в рівнянні: 2х-3 - х-7?
а)2х-3-х-7 = 0; б)2х-х=-7-3; в)-2х+х=-7+3; т)2х-х=7+3.
2. Поясніть кожний крок розв'язування рівняння:
7х-14=5х; 7x-5x=14; 2x=4; х=14:2; х=7.
Письмові вправи
Перенесіть із лівої частини рівняння в праву доданок, що не містить
невідомого: а)-5х+1,2=2х+11; б) 4х-9=-x-5,2.
Перенесітьуліву частину рівняння всі доданки, що містять невідоме, а в праву, що не містять невідомого: а) 17х-5=8x+5,6; б)-11у+7 =-3у-10.
Розв'яжіть рівняння: а)7х-5=6х+1; б)4х-3 = 2х+5; в)9-8у=-6у+1;
г)6m+3=7m+8; д)-9m-2=9m-2; е)-9а+6=-10a+15;
ж) 4y+7=-5+4y; з) 0,7х+1,6=-0.1х; к) -4,5х-3 = 2,7х+15; л)39-7y+17=3y+16; м)15-6x=2x-5х-3.
Перш ніж переносити доданки, треба спростити вирази в правій та лівій частинах окремо (звести подібні доданки, якщо вони є).
- Підсумок уроку.
Які властивості рівняння ви знаєте?
Назвати корінь рівняння.
х+5=х+5;
х+5=х-2.
8 Домашнє завдання №54,56.
10 клас.
Тема: Степенева функція, її властивості і графік.
Мета: Ввести означення степеневої функції, розглянути її властивості і графіки. Систематизація та узагальнення поняття стпеневої функції. Формування навичок і вмінь розв’язувати задачі. Розвивати логічне мислення, чіткість побудов логічних зв’язків.. Виховувати уважність, акуратність, спостережливість, чіткість побудов графіків.
Хід уроку:
- Організаційний момент.
Оголошення теми, мети.
- Перевірка домашнього завдання
Біля дошки з коментуванням та повторенням теоретичного матеріалу.
- Актуалізація опорних знань.
Що називається степенем з натуральним і цілим показником?
Що називається степенем з раціональним показником?
Назвіть властивості степеня з раціональним показником.
Що називається степенем з ірраціональним показником?
- Узагальнення вивченого матеріалу.
Виклад матеріалу проводиться у вигляді бесіди. Вчитель разом з учнями будують графіки функцій, з’ясовують їх властивості.
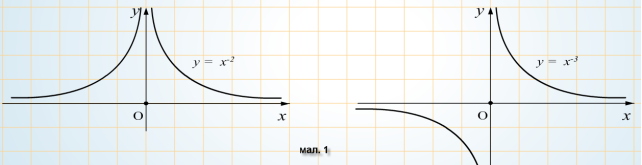
 Степенева функція та її властивості.
Степенева функція та її властивості.
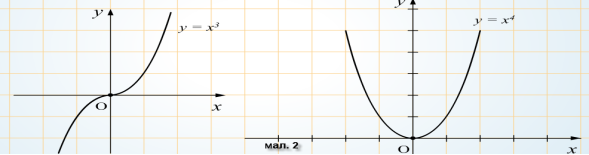
![]()
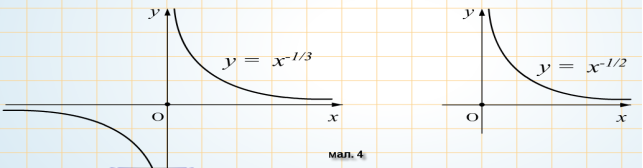
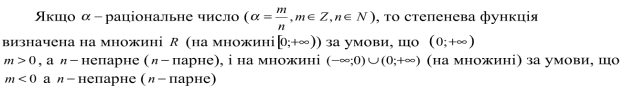
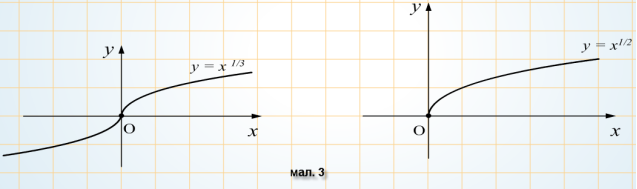
![]()
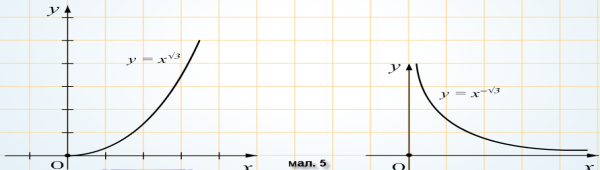
5.Закріплення вивченого. Розв’язування вправ
Приклад 1. Знайти область визначення функції
Б)![]()
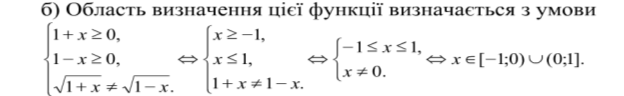
Приклад 2.Побудувати графік функції
А)![]() ; б)
; б) ![]()


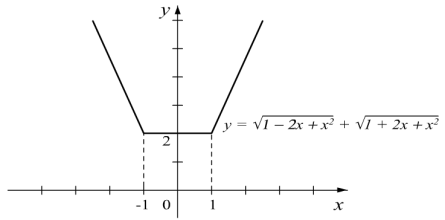

Робота в групах. (4 учні в групі.)

6.Підсумок уроку.
Провести підсумок уроку, оцінювання учнів
7.Домашнє завдання №35, 36, 37, 39.


про публікацію авторської розробки
Додати розробку
