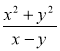Додавання і віднімання дробів з однаковими знаменниками
Тема. Додавання і віднімання дробів з однаковими знаменниками
Мета: домогтися засвоєння учнями змісту правила додавання і віднімання раціональних дробів з протилежними знаменниками та схеми його застосування; сформувати вміння відтворювати ці правила та застосовувати їх для перетворення суми або різниці дробів із протилежними знаменниками на раціональний дріб, удосконалити вміння застосовувати правило знаків та алгоритм скорочення раціональних дробів.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання: опорний конспект «Додавання і віднімання раціональних дробів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
- Виконання письмових вправ перевіряємо тільки в учнів, які потребують додаткової педагогічної уваги (зібрати зошити або дати завдання перевірити сильним учням за зразком).
- Тестова робота № 2
Варіант 1
-
Чому дорівнює різниця
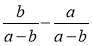 ?
?
|
А |
Б |
В |
г |
|
|
-1 |
1 |
|
-
Виконайте віднімання:
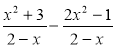 .
.
|
А |
Б |
В |
Г |
|
2 – х |
2 + х |
|
|
-
Спростіть вираз
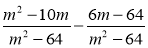 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Варіант 2
-
Чому дорівнює різниця
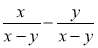 ?
?
|
А |
Б |
В |
Г |
|
|
|
1 |
-1 |
-
Виконайте віднімання:
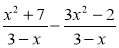 .
.
|
А |
Б |
В |
Г |
|
|
|
3 – х |
3 + х |
-
Спростіть вираз
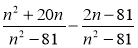 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
III. Формулювання мети і завдань уроку
З метою створення позитивної мотивації діяльності учнів та усвідомлення змісту навчальної проблеми, винесеної на урок, можна запропонувати учням розв'язання двох завдань, пов'язаних за змістом: одне із завдань передбачає виконання дій у стандартній ситуації, що розглядалася на попередньому уроці (додавання або віднімання раціональних дробів з однаковими знаменниками), а друге - виконання дій у зміненій ситуації (віднімання або додавання двох дробів, один з яких дорівнює першому дробу з першого завдання, а другий дріб має знаменник, протилежний знаменнику другого дробу з першого завдання). Якщо матеріал попередньої теми опрацьовано добре (і правильно виконана відповідна частина домашнього завдання), то під час порівняння умов завдання № 1 і № 2 учні мають побачити, що знаменники цих дробів є протилежними виразами, а тому сформулювати проблему: «Чи можна правила додавання і віднімання раціональних дробів з однаковими знаменниками застосувати у випадку, якщо знаменники раціональних дробів є протилежними виразами? Якщо це можливо, то як це можна зробити»? Звісно, пошук відповіді на це запитання і становитиме основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття матеріалу перед вивченням питання уроку слід активізувати знання і вміння учнів щодо перетворень цілих виразів, знаходження виразу, протилежного даному, властивості степенів протилежних виразів із парним (або непарним) показником, а також скорочення раціональних дробів та перетворення суми або різниці раціональних дробів у раціональний дріб.
Виконання усних вправ
- Укажіть допустимі значення змінних виразу:
а) х2 + 1; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
- Виконайте дії:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Чи є тотожністю рівність: а)
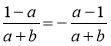 ; б)
; б) 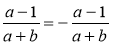 ;
;
в) ![]() ; г)
; г) 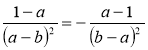 ; д)
; д) 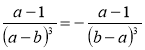 ?
?
V. Засвоєння знань
План вивчення нового матеріалу
1. Правило додавання і віднімання раціональних дробів з протилежними знаменниками. Алгоритм перетворення.
2*. Зворотне перетворення раціонального дробу в суму або різницю раціональних дробів з тим самим знаменником.
3. Приклади застосування вивчених алгоритмів.
Формулювання правила додавання і віднімання раціональних дробів з протилежними знаменниками після виконаної роботи з повторення не викликає труднощів і може бути сформульоване самими учнями як словесно, так і у вигляді формули
![]()
яка справджується при всіх допустимих значеннях змінних у виразі. Зазначене правило не потребує доведення, тому після його формулювання складаємо схему дій та ілюструємо її застосування прикладами. Особливу увагу звертаємо на ряд випадків, про які слід поговорити окремо: випадки додавання або віднімання раціональних дробів, знаменники яких є степенями протилежних виразів.
Під час розв'язування деяких завдань достатнього та високого рівнів складності доречно виконати перетворення раціонального дробу в суму або різницю цілого виразу та раціонального дробу. Тому вже на цьому уроці можна розглянути з учнями перетворення, що виражається тотожністю ![]() . Застосування цієї тотожності демонструється у процесі розв'язуванні відповідних прикладів.
. Застосування цієї тотожності демонструється у процесі розв'язуванні відповідних прикладів.
VI. Засвоєння умінь
Виконання усних вправ
- Перетворіть у дріб вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Доведіть, що при будь-яких значеннях а додатним є значення виразу:
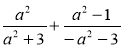 .
.
-
Скоротіть дріб: а)
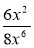 ; б)
; б) 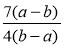 ; в)
; в)  ; г)
; г) 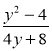 .
.
Виконання письмових вправ
Вправи, що пропонуються для розв'язання на цьому уроці, мають сприяти формуванню сталих навичок:
• додавання та віднімання дробів з протилежними знаменниками (із використанням правила знаків та правил додавання і віднімання раціональних дробів з однаковими знаменниками);
• застосовування правила додавання і віднімання раціональних дробів з однаковими знаменниками «справа наліво» для виділення з дробу цілого виразу.
Для реалізації дидактичної мети уроку на цьому уроці слід розв'язати завдання такого змісту.
- Перетворення у раціональний дріб суми або різниці раціональних дробів із протилежними знаменниками у раціональний дріб.
1) Спростіть вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Спростіть вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; е)
; е) 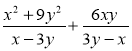 .
.
3) Доведіть, що при всіх допустимих значеннях х значення виразу не залежить від х: а) ![]() ; б)
; б) ![]() .
.
- Перетворення суми або різниці раціональних дробів (знаменники містять степені протилежних виразів) у раціональний дріб. Спростіть вираз:
а) 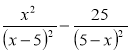 ; б)
; б) 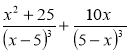 .
.
- Запис раціонального дробу у вигляді суми або різниці цілого виразу й раціонального дробу.
1) Користуючись тотожністю ![]() , подайте дріб у вигляді суми дробів: а)
, подайте дріб у вигляді суми дробів: а) ![]() ; б)
; б) 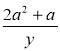 ; в)
; в) 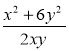 ; г)
; г) 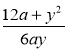 .
.
2) Подайте дріб у вигляді суми або різниці цілого числа і дробу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
- Виконання вправ на повторення: знаходження суми або різниці раціональних дробів з однаковими знаменниками, скорочення раціональних дробів, знаходження ОДЗ раціонального дробу.
1) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2) Скоротіть дріб: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) 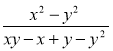 ; є)
; є) ![]() .
.
3) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) 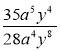 ; є)
; є) 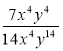 .
.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Відомо, що а – b = 9. Знайдіть значення дробу:
а) 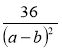 ; б)
; б) 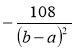 ; в)
; в) 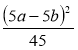 ; г)
; г) ![]() .
.
2) Знайдіть пропущений вираз:
|
|
|
|
|
|
|
? |
VII. Підсумки уроку
Серед наведених рівностей виберіть правильну. Поясніть свій вибір.
1) ![]() ;
;
2) ![]() ;
;
3) 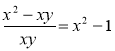 .
.
VIII. Домашнє завдання
- Вивчити схему дій, що дозволяє виконувати додавання та віднімання дробів із протилежними знаменниками.
- Виконати вправи на закріплення навичок додавання та віднімання дробів із протилежними знаменниками та застосування правил додавання і віднімання дробів з однаковими знаменниками у зворотному напрямку.
- На повторення: вправи на відновлення вмінь зводити дроби до нового знаменника та на розкладання многочленів на множники.


про публікацію авторської розробки
Додати розробку