Додавання і віднімання дробів з різними знаменниками
Тема. Додавання і віднімання дробів з різними знаменниками
Мета: домогтися засвоєння учнями змісту поняття «(найменший) спільний знаменник» для даних раціональних дробів, змісту алгоритму знаходження найменшого спільного знаменника для раціональних дробів, а також алгоритму додавання і віднімання раціональних дробів із різними знаменниками; сформувати вміння відтворювати вивчені алгоритми та виконувати дії за цими алгоритмами для запису суми або різниці раціональних дробів із різними знаменниками у вигляді (нескоротного) раціонального дробу.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання: опорний конспект «Додавання і віднімання раціональних дробів».
Хід уроку
I. Організаційний етан
II. Перевірка домашнього завдання
На початку уроку вчитель збирає на перевірку зошити з виконаним домашнім завданням (щоб перевірити засвоєння учнями знань та вмінь з теми «Додавання та віднімання дробів з однаковими знаменниками» та, за умови успішного виконання, оцінити роботу учнів) або, організувавши роботу учнів з перевірки домашнього завдання за зразком та скорегувавши можливі помилки, пропонує учням виконати завдання аналогічного змісту (тестова робота № 3).
Тестова робота № 3
Варіант 1
-
Чому дорівнює сума
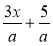 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть різницю дробів
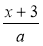 і
і 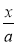 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть суму дробів
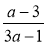 і
і 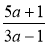 .
.
|
А |
Б |
В |
Г |
|
|
1 |
2 |
|
4. Виконайте додавання: ![]() .
.
|
А |
Б |
В |
Г |
|
-1 |
|
|
0 |
Варіант 2
-
Чому дорівнює сума дробів
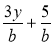 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть різницю дробів
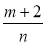 і
і 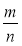 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть суму дробів
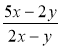 і
і 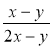 .
.
|
А |
Б |
В |
Г |
|
3 |
|
3х – 3 |
|
-
Знайдіть суму дробів
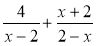 .
.
|
А |
Б |
В |
Г |
|
|
х |
|
-1 |
III. Формулювання мсти і завдань уроку
Свідомому сприйняттю мети уроку може сприяти бесіда, в ході якої учні відповідатимуть на такі запитання вчителя:
- Як додати (відняти) звичайні дроби з однаковими знаменниками?
- Як виконується додавання (віднімання) звичайних дробів із різними знаменниками?
- Як додати (відняти) раціональні дроби з однаковими знаменниками? Чи схоже це правило на відповідне правило для звичайних дробів?
- Чи можна раціональний дріб подати у вигляді рівного йому раціонального дробу з іншим знаменником? Як це зробити (як називається така дія та який механізм її виконання)?
Після закінчення бесіди учні мають усвідомити, що важливого значення набуває вивчення додавання і віднімання раціональних дробів з різними знаменниками. Вивчення питання про можливість виконання та алгоритм додавання (віднімання) раціональних дробів із різними знаменниками с основною дидактичною метою уроку.
IV. Актуалізація опорних знань та вмінь
Відповідно до обговорених на попередньому етапі моментів перед вивченням нового матеріалу слід активізувати знання і вміння учнів щодо виконання додавання і віднімання звичайних дробів із різними знаменниками, розкладання многочленів на множники, зведення раціонального дробу до нового знаменника, а також перетворення суми або різниці раціональних дробів на раціональний дріб.
Виконання усних вправ
-
Зведіть дроби:
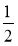 ;
; 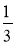 ;
; 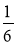 ;
; 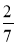 ;
; 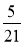 до знаменника 42.
до знаменника 42.
- Подайте вирази у вигляді добутку:
а) 10х + 15у; б) а2 – 25; в) 42у2 – 21у; г) 7х2 – 7у2; д) 6m – 2n; є) 16x – xy;
ж) а2 – 4а + 4; з) а8 – a7.
- Який знаменник є найменшим спільним знаменником для дробів:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ?
?
- Яке число слід підставити замість *, щоб утворилась тотожність:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 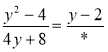 ?
?
V. Засвоєння знань
План вивчення нового матеріалу
1. Поняття спільного знаменника для раціональних дробів.
2. Алгоритми зведення дробів до спільного знаменника.
3.* Загальне правило додавання та віднімання раціональних дробів із різними знаменниками.
Вивчення питання про додавання та віднімання раціональних дробів із різними знаменниками слід розпочати якраз із формування уявлення учнів про зміст поняття найменшого спільного знаменника поданих раціональних дробів та способу його знаходження. При цьому можна для наочності використовувати знання учнів щодо способів знаходження найменшого спільного знаменника звичайних дробів та алгоритму зведення раціонального дробу до нового знаменника (див. вище). Розглянувши типові випадки знаходження спільного знаменника для раціональних дробів, можна узагальнити спостереження, склавши алгоритм відшукання найменшого спільного знаменника для пропонованих раціональних дробів. Складений алгоритм слід «випробувати» на розглянутих раніше прикладах. Після вивчення питання про знаходження спільного знаменника повторюємо алгоритм зведення раціональних дробів до нового знаменника та об'єднуємо їх у загальний спосіб дій під назвою «зведення раціональних дробів до спільного знаменника».
Розглянувши питання про зведення раціональних дробів до спільного знаменника, переходимо до вивчення питання про застосування цих дій під час додавання або віднімання раціональних дробів із різними знаменниками: складається алгоритм додавання і віднімання раціональних дробів із різними знаменниками. При цьому слід зробити акцент на тому, що цей алгоритм ґрунтується на відомому алгоритмі додавання і віднімання раціональних дробів з однаковими знаменниками, до якого додано алгоритм зведення раціональних дробів до спільного знаменника.
Під час вивчення теми можуть виникнути труднощі, зумовлені, крім усього іншого, ще й тим, що додавання та віднімання дробів із різними знаменниками передбачає більш довгу послідовність дій, що потребує достатньо розвиненої уваги учнів та вміння переключатись з одного алгоритму на інший. При цьому слід зауважити, що в деяких учнів на початку вивчення теми виникають труднощі саме тому, що названі психологічні механізми ще недостатньо розвинені. Тому вчитель, уже виходячи із знання рівня підготовки учнів, може прийняти рішення про те, чи слід на цьому уроці вивчати алгоритми зведення дробів до спільного знаменника і додавання та віднімання дробів із різними знаменниками, чи зосередитись на цьому уроці тільки на одному алгоритмі зведення дробів до нового знаменника і відпрацювати стійкі вміння його застосування, а вже на наступному уроці розпочати вивчення алгоритму додавання та віднімання дробів із різними знаменниками (див. 3) плану).
VI. Засвоєння вмінь
Виконання усних вправ
Знайдіть найменший спільний знаменник дробів:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() ; д)
; д) ![]() і
і ![]() ; є)
; є) ![]() і
і ![]() .
.
Із названих пар дробів виберіть ті, що мають спільним знаменником:
а) добуток їхніх знаменників;
б) один із знаменників поданих двох дробів;
в) вираз, складений з усіх різних множників знаменників даних дробів.
Виконання письмових вправ
*Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту.
-
Зведення до (найменшого) спільного знаменника раціональних
дробів.
1) Зведіть до спільного знаменника дроби:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() ; д)
; д) ![]() і
і ![]() ;
;
є) ![]() і
і ![]() ; ж)
; ж) ![]() і
і ![]() ; з)
; з) ![]() і
і ![]() .
.
2) Зведіть до спільного знаменника дроби:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() .
.
-
Зведення до (найменшого) спільного знаменника та додавання або
віднімання раціональних дробів із різним знаменниками.
1) Подайте у вигляді дробу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Виконайте додавання (віднімання) дробів:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) ![]() .
.
3) Виконайте додавання (віднімання) дробів:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() : є)
: є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() ;
;
и) ![]()
4) Спростіть вираз:
а) ![]() б)
б) ![]() ; в)
; в) ![]() .
.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Знайдіть числа а і b, за яких рівність виконується при всіх допустимих значеннях х.
а) ![]() ; б)
; б) ![]() .
.
2) У двох посудинах місткістю по 10 л разом було 10 л концентрованої кислоти. Першу посудину долили доверху водою і здобутою сумішшю доповнили другу посудину. Після цього у другій посудині стало кислоти на 5 л більше, ніж у першій. Скільки кислоти було в кожній посудині спочатку?
3) Знайдіть пропущений вираз:
|
|
|
42 |
|
|
|
7 |
- Виконання вправ на повторення: завдання на закріплення та вдосконалення вмінь виконувати перетворення раціональних дробів, вивчені раніше.
1) При яких значеннях змінної вираз не має змісту:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3) Спростіть вираз:
а) ![]() ; б)
; б) 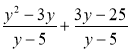 ; в)
; в) ![]() .
.
Вправи, що пропонуються для розв'язування на цьому уроці, мають сприяти формуванню сталих навичок:
- знаходження найменшого спільного знаменника та зведення до цього спільного знаменника дробів зі знаменниками - одночленами (різного рівня складності);
- знаходження найменшого спільного знаменника та зведення до нього спільного знаменника дробів, знаменники яких є многочленами (від лінійних виразів до виразів вищих степенів, що потребують попереднього розкладання на множники).
Під час розв'язування вправ слід постійно слідкувати за дотриманням учнями правильної послідовності дій, передбачених алгоритмом зведення дробів до спільного знаменника: спочатку знаходимо спільний знаменник, потім знаходимо додаткові множники для кожного з дробів, а вже після цього знаходимо дроби з новим спільним знаменником, що дорівнюють даним).
VII. Підсумки уроку
Серед рівностей виберіть правильну. Поясніть свій вибір.
-
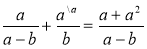 ;
;
-
 ;
;
-
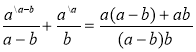 ;
;
-
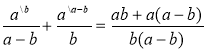 .
.
VIII. Домашнє завдання
- Вивчити схему дій, що дозволяє виконувати зведення дробів до нового знаменника.
- Виконати вправи на закріплення навичок пошуку найменшого спільного знаменника та зведення дробів до спільного знаменника.
- На повторення: вправи на відновлення вмінь виконувати додавання та віднімання дробів із протилежними знаменниками та додавання і віднімання дробів з однаковими знаменниками.


про публікацію авторської розробки
Додати розробку
