Додавання раціональних чисел з різними знаками.
Тема. Додавання раціональних чисел з різними знаками.
Мета: сформувати уявлення учнів про зміст дії додавання раціональних чисел з різними знаками (в тому числі й протилежних чисел), а також виробити вміння використовувати це правило під час додавання двох раціональних чисел з різними знаками.
Обладнання: демонстраційний термометр.
Тип уроку: засвоєння навичок та вмінь.
Хід уроку
I. Перевірка домашнього завдання
Математичний диктант
Варіант 1 [2]
- Чому дорівнює сума чисел -7 та -3 [-6 та -5]?
- Чому дорівнює сума чисел -175 та -314 [-217 та -522]?
-
Чому дорівнює сума чисел -
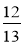 та -
та -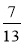 [-
[-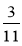 та -
та -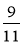 ]?
]?
-
Чому дорівнює сума чисел -2
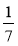 та -4
та -4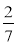 [-3
[-3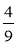 та -2
та -2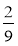 ]?
]?
- Чому дорівнює сума модулів чисел -25 та-18 [-34 та -28]?
- Чому дорівнює модуль суми чисел -25 та -18 [-34 та -28]?
II. Актуалізація опорних знань
Усні вправи
-
Обчисліть: а) 76 – 3; 76 – 30; 0,76 – 0,3; 0,76 – 0,03;
б) 254 – 2; 25,4 – 2; 25,4 – 0,2; 2,54 – 2;
в) 82 – 2; 0,82 – 0,2; 0,82 – 0,02; 8,2 – 0,02;
г) 5,7 – 1,3; 8 – 3,4; 12,3 – 1,8; 10,273 – 5,49.
- Знайдіть серед чисел: а) від'ємні; б) додатні.
+5; -(+5); -(-2,3); -(+2,3); 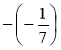 ;
; 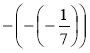 .
.
-
Назвіть модулі чисел. Випишіть те, яке має більший модуль:
а) -5,8 та + 7,8; б) -2,75 та 1,3; в) -7,1 та 71; г) -2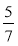 та 3
та 3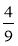 ;
;
д) -![]() та
та ![]() ; є) -
; є) -![]() та
та ![]() .
.
III. Застосування знань
- Мотивація навчальної діяльності
Цей урок є другим у темі «Додавання раціональних чисел» і на попередньому уроці було розглянуто питання додавання чисел з однаковими знаками. Тому логічним продовженням (і учні повинні це усвідомити) є питання додавання раціональних чисел з різними знаками. Зрозуміло, що як і на попередньому уроці ми спочатку розв'язуємо задачі на координатній прямій (шкала демонстраційного термометра), а потім вже на основі спостережень формулюємо загальні правила додавання чисел з різними знаками.
Важливо також пояснити учням, що додавання чисел за допомогою координатної прямої не є зручним, ми звертаємось до цього способу лише для того, щоб на прикладах побачити певні закономірності, які сформуємо в загальні правила обчислення сум раціональних чисел.
-
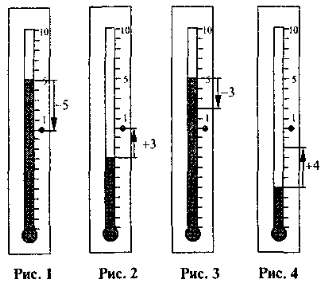 Додавання двох протилежних чисел
Додавання двох протилежних чисел
Задача 1. Вранці температура повітря була +5°С. За день вона знизилась на 5°С. Якою стала температура повітря ввечері?
Розв'язання. Зрозуміло, що, ввечері температура стала 0°С (див. рис. 1). Отже, зниження температури означає -5. Тоді задачу можна розв'язати додаванням: +5 + (-5) = 0.
Задача 2. Вранці температура повітря була -3°С, за день вона підвищилась на 3°С. Якою стала температура за день?
Розв'язання. Зрозуміло, що ввечері температура стала 0°С (див. рис. 2). Отже, задачу можна розв'язати додаванням: -3 + (+3) = 0.
Бачимо, що сума протилежних чисел дорівнює 0. Наприклад, -7 + 7 = 0; 3,5 + (-3,5) = 0; a + (-a) = 0.
- Додавання двох раціональних чисел зрізними знаками
Задача 3. Термометр показував температуру +5°С, а потім вона знизилась на 3°С. Яку температуру показує термометр зараз?
Розв'язання. Зрозуміло, що зараз термометр показує +2°С (див. рис. 3). Зниження температури позначимо -3, тоді задачу можна розв'язати додаванням: 5 + (-3) = 2.
Звернемо увагу, що (+5) + (-3) = + (|5| - |3|) = + (5 - 3) = +2.
Задача 4. Термометр показував температуру-6 °С, а потім вона підвищилась на 4°С. Яку температуру повітря показує термометр зараз?
Розв'язання. Зрозуміло, що температура стала -2°С (див. рис. 4). Підвищення температури позначаємо +4°С. Тоді задачу можна розв'язати додаванням: -6 + (+4) = -2. Отже, -6 + (+4) = -(|6| - |+4|) = -(6 – 4) = -2.
Таким чином, щоб додати два числа з різними знаками, треба:
- від більшого модуля відняти менший;
-
поставити перед здобутим числом знак того числа, в якого модуль
більший.
Зауваження. Зазвичай спочатку визначають і записують знак суми, а потім знаходять значення різниці модулів.
Наприклад: -20 + (+15) = - (20 - 15) = -5; -20 + (+25) = + (25 - 10) = +5
Бажано вимагати від учнів, починаючи з першого уроку, точного відтворення алгоритму додавання чисел з різними знаками, бо, як показує досвід, недбале ставлення до знань алгоритмів (особливо це стосується правил дій з раціональними числами) призводить у підсумку до великих проблем під час виконання обчислень як у шостому, так і в старших класах.
IV. Закріплення знань. Вироблення вмінь
Усні вправи
- Виконайте додавання:
а) (+3) + (-3); б) (-9) + (+9); в) ![]() +
+![]() ; г) -3
; г) -3![]() + 3
+ 3![]() .
.
-
Чи правильно виконано додавання? (Прочитайте і прокоментуйте
рівність): а) -15 + (+10) = 15 - 10 = 5; б) -15 + (+10) = - (15 + 10) = -25;
в) -15 + (+10) = - (15 - 10) = -5.
- Виконайте додавання: а) 9 + (+5); -9 + (-5); -9 + (+5); +9 + (-5);
б) 10 + (+4); -10 + (-4); -10 + 4; +10 + (-4);
в) -0,6 + (+0,2); +0,6 + (-0,2); -0,6 + (-0,2); 0,6 + (+0,2).
Вимагаємо від учнів відтворення відповідних алгоритмів.
Письмові вправи
- Виконайте додавання:
а) 26 + (-6); б) -70 + 50; в) -17 + 30; г) +80 + (-120);
д) -6,3 + 7,8; є) -9 + 10,2; ж) 1 + (-0,39); з) 0,3 + (-1,2);
к) ![]() +
+![]() ; л)
; л) ![]() +
+![]() ; м) -
; м) -![]() +
+![]() ; н) -
; н) -![]() +
+![]() ; о) -3
; о) -3![]() +2
+2![]() ;
;
п) -![]() +5
+5![]() ; р) 2
; р) 2![]() +
+ ; с) 5
; с) 5![]() +
+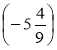 .
.
- Додайте: а) до суми -6 та -12 число 20;
б) до числа 2,6 суму -1,8 та 5,2;
в) до суми -10 та -1,3 суму 5 та 8,7;
г) до суми 11 та -6,5 суму -3,2 та -6.
Додаткові вправи
-
Скільки цілих чисел розташовано між числами:
а) 0 та 24; б)-12 та -3; в) -20 та 7? - Подайте число -10 у вигляді суми двох від'ємних доданків, щоб:
а) обидва доданки були цілими числами;
б) обидва доданки були десятковими дробами;
в) один з доданків був правильним звичайним дробом.
-
Яка відстань (в одиничних відрізках) між точками координатної
прямої з координатами:
а) 0 та а; б) -а та а; в) –а та 0; г) а та -3а?
V. Підсумки уроку
Запитання до класу
- Який знак має сума двох чисел з різними знаками?
- Чому дорівнює модуль суми двох чисел з різними знаками?
- Як виконати додавання двох чисел, з яких одне - додатне, друге - від'ємне?
- Сума яких двох чисел дорівнює 0?
- Поставте знаки доданків так, щоб рівність була правильною:
а) ...3 + ...5 = +8; б) ...3 + ...5 = -8; в) ...3 + ...5 = +2; г) ...3 + ...5 = -2.
VI. Домашнє завдання
- Виконайте додавання:
а) 17 + (-5); б) -21 + 19; в) -8 + (-43); г) -15 + (-18); д) -0,5 + 6;
є) -2,4 + (-3,2); ж) -3,84 + 4,16; з) -![]() +
+![]() ; к) -
; к) -![]() +
+![]() ; л)
; л) ![]() +
+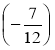 ;
;
м) -1+![]() ; н) -2 + 1
; н) -2 + 1![]() ; о) 3+
; о) 3+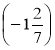 ; п) 2
; п) 2![]() +
+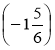 ; р) -5
; р) -5![]() + 4,5.
+ 4,5.
- Порівняйте у вигляді суми двох рівних доданків числа:
10; -8; -6,8; -![]() ; -3
; -3![]() ; -1
; -1![]() .
.
-
Задача. У складі товарного потяга 42 вагони. Закритих вагонів було в 1,3 раза більше, ніж платформ, а число цистерн становило
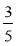 числа платформ. Скільки вагонів кожного виду було у складі потяга?
числа платформ. Скільки вагонів кожного виду було у складі потяга?

про публікацію авторської розробки
Додати розробку
