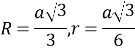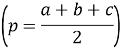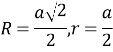Допоміжний матеріал до розв'язування задач з тем: "Перпендикулярність у просторі", "Многогранники"

ДОПОМІЖНИЙ МАТЕРІАЛ ДО РОЗВ’ЯЗУВАННЯ ЗАДАЧ

З ТЕМ: «ПЕРПЕНДИКУЛЯРНІСТЬ У ПРОСТОРІ», «МНОГОГРАННИКИ»

Формули залежності сторони многокутника та радіусів

описаного (R) навколо нього та вписаного (r) в нього кола

Запам’ятайте:

1.В прямокутному трикутнику центр описаного кола лежить на середині гіпотенузи.

2.В квадраті центри описаного та вписаного кіл лежать в точці перетину діагоналей.

3.В правильному трикутнику центри описаного та вписаного кіл лежать в точці перетину медіан.

4.В довільному трикутнику центр описаного кола лежить в точці перетину серединних перпендикулярів його сторін, а центр вписаного кола – в точці перетину бісектрис  внутрішніх кутів трикутника.

Вивчіть правила:

Якщо точка рівновіддалена від вершин многокутника, то вона проектується в центр описаного кола (шукаємо R).

Якщо точка рівновіддалена від сторін многокутника, то вона проектується в центр вписаного кола (шукаємо r).