Допоміжний матеріал до уроку «Декартові координати точки у просторі»

Допоміжний матеріал до уроку «Декартові координати точки у просторі»

Шановні десятикласники!

На цьому уроці я пропоную вам дві задачі, пов’язані з декартовими координатами у просторі.

Задача 1.

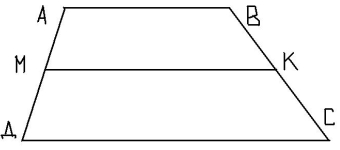
Знайти довжину середньої лінії трапеції АВСД з вершинами А(3;2;0), В(–3;2;0), С(1;3;4), Д(–1;3;4), і основами АВ і СД.

Розв’язання. В першу чергу звертаємо увагу на основи трапеції, адже, як правило, їх позначають АД і ВС.

Для знаходження довжини середньої лінії (МК) ми повинні знайти координати точок М і К, як середин сторін АД і ВС.

1) = ; аналогічно для і

= =1;  = = 2,5;  = = 2;           М(1;2,5;2)

= ; аналогічно для і

= = –1;  = = 2,5;  = = 2;       К(–1;2,5; 2)   

МК =   = = 2

МК = 2

Задача 2.

Точки М(3; – 2; 1) і К(–1;6;3) середини сторін АВ і ВС трикутника АВС відповідно. Знайти координати точок В і С, якщо А(5; –1;1).

Розв’язання.

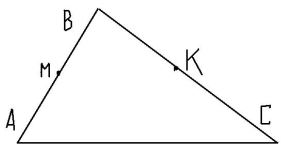
Задача зводиться до знаходження координат другого кінця відрізка, якщо відомі координати його середини і іншого кінця.

= , тоді 2 = + , тобто = 2 – ; аналогічно для і .

= 2*3 – 5 = 1; = 2*(–2) – (–1) = –3; = 2*1 – 1 = 1; В(1; –3; 1)

Бажаю успіху!