Управління освіти, науки, молоді та спорту  Кіровоградської обласної державної адміністрації 

Комунальний заклад « Кіровоградський обласний інститут післядипломної педагогічної освіти імені Василя Сухомлинського»

Завдання ІІ туру Всеукраїнської олімпіади з математики

10  клас

1.   Розв’яжіть рівняння  -10-2(а-11) +2(5а+6)х+2а +=0.

2.   Робочий день скоротився з 8 год. до 7 год. На скільки відсотків потрібно підняти продуктивність праці, щоб при тих самих розцінках заробітна плата зросла на 5%?

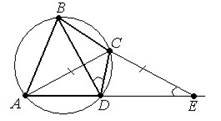
3.   На продовженні сторони AD вписаного чотирикутника ABCD за точку D відмітили точку E так, що AC CE і BDC DEC . Відомо, що DE1см Знайдіть довжину сторони AB.

4.   У класі 28 учнів. Середній зріст всіх учнів цього класу дорівнює 150 см. Середній зріст всіх хлопчиків дорівнює 155 см, а середній зріст всіх дівчаток дорівнює 148 см. Скільки дівчаток в цьому класі? Відповідь обґрунтуйте.

5.   Вісім однакових кубиків з ребром, довжина якого дорівнює 1, зафарбували так, що 24 їхні грані білі, а 24 – чорні. Доведіть, що з них можна скласти куб, у якого площа частини поверхні, зафарбованої білою фарбою, така ж, як площа частини поверхні, зафарбованої чорною фарбою.

                                 Кожне завдання оцінюється в 5 балів

На виконання завдань відводиться 3 години

Використання калькуляторів заборонено 2017 рік

Відповіді:

1. Розв’язання: Ліва частина рівняння є квадратним тричленом відносно параметра а. Тому рівняння запишемо так:

–2а(–5x–1)+(x⁴–10+22+12х)=0. Оскільки його дискримінант невід’ємний: D/4=, то маємо рівняння + 10а+25=0, якщо х=1, і (а–+ 6х)(а–в іншому разі. У першому випадку а= –5 і дане рівняння набуває вигляду –10+32–38х+15=0 (х–3)(х–5)=0.

Звідси маємо 4 корені рівняння: 1, 1, 3, 5. У випадках, коли а5 маємо сукупність квадратних рівнянь –6х–а=0 і –4х–2–а=0. Розв’язки даного рівняння, залежно від параметра такі:

                                а                                       х

                                      (–                       розв’язків немає

                                        –9                                                       3; 3

                                       (–9;–6)                                             3

                                           –6                                                 3, 2, 2

                                          –5                                                 1, 1, 3, 5

                                   (–6;–5)(–5;                            

2.  Розв’язання: За 1 годину восьмигодинного робочого дня робітник виконував 1/8 частину норми, що приймемо за 100%. За 1 годину семигодинного робочого дня він вже виконував 1/7 частину норми, що складає %.  Продуктивність роботи  зросла на  Це підвищення продуктивності зберегло розмір заробітної плати. Для підвищення заробітної плати на 5%  продуктивність праці треба підвищити на    або 15%. Відповідь:  15%.

3.  Розв’язання:

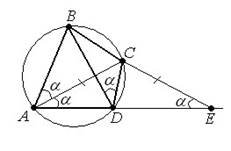Нехай DEC, тоді DAC DEC  як кути при основі рівнобедреного трикутника. BDC за умовою задачі; BAC BDC  як вписані кути, що спираються на одне і ту саму дугу.

Крім             того,             помічаємо,             що

ABC180ADC CDE . Тоді трикутники ABC і EDC рівні за двома сторонами і кутом між ними. Отже, AB DE 1см.

Відповідь:  AB1см.

4.  Розв’язання: Нехай m – кількість хлопчиків в цьому класі, а d – кількість дівчаток. Тоді сумарний зріст усіх хлопчиків дорівнює S=m155 см, а сумарний зріст всіх дівчаток дорівнює s =d148 см. Отже, сумарний зріст всіх учнів цього класу S+ s= m155+ d148 (см), а з іншої сторони в класі 28 учнів і середній зріст їх дорівнює 150см, тоді сумарний зріст всіх учнів дорівнює 28150=4200см. Отже  m+ d=28 і  (28–d)155+ d148=4200.

Розв’язавши рівняння, одержимо d=20. У класі 20 дівчаток.

Відповідь: 20.

5.  Розв’язання.Складаємо куб довільним чином. Нехай на його поверхні буде а білих і b чорних квадратів. Зрозуміло, що  а+b=24. Розглянемо число  х= а– b. Воно парне. Якщо х=0, то а= b, і задача розв’язана. В іншому разі поворот одного з кубиків на кут  відносно однієї з осей, що проходить через центри протилежних граней, залишає число х незмінним або змінює його на 2.  За три такі операції можна досягти, щоб грані кубика, які були на поверхні куба, сховалися всередину, а ті, що були всередині, опинилися на поверхні. За 24 такі операції число х дорівнюватиме 

(24 – а) – (24 – b) = b – а = –( а – b), тобто стане протилежним початковому значенню. Отже, на якомусь кроці воно дорівнюватиме нулю.