Дорогами математики. Практичний посібник
Розділ виставки:
Шляхи підвищення якості природничо-математичної освіти
Дорогами математики
(з досвіду роботи, практичний посібник)
Автор: Пустовгар Олександр Миколайович
Посада: вчитель математики
Категорія: «спеціаліст вищої категорії»
 |
Скориківська загальноосвітня школа I-III ступенів Золотоніської районної ради
Рецензент: Пономарьова О.І.- методист відділу освіти Золотоніської районної державної адміністрації
Анотація
У роботі розкрито практичні питання покращення стану викладання математики, зокрема, методику індивідуалізації роботи учнів на уроці, представлено розробки уроків з алгебри та геометрії, матеріали для позаурочної роботи з математики.
Робота буде цікава вчителям математики, інших предметів та всім небайдужим до цієї науки.
Матеріали схвалені методичною радою відділу освіти Золотоніської районної державної адміністрації (протокол №3 від 24.02.2012
року)
Зміст
1.Коротко про головне. 5
2.Можливо це буде Вам у нагоді. 9
3. Два погляди на урок:
а) Урок геометрії у 7 класі «Ознаки паралельності
прямих» 15
б) Урок алгебри у 11 класі «Розв’язування
показникових рівнянь» 21
4. Про математику жартома і всерйоз:
а) «Тиждень математики в школі» 27
б) Матеметичний КВК
в) «Математичні чудеса та таємниці» 34
г) Математичний міні-концерт 48
5. Світлини для історії 56
6. Список використаних джерел …………………………………………60 «Знати свою науку вчителю, звичайно, необхідно, але, крім цього, потрібно ще володіти ключем до розуму і серця своїх вихованців.»
невеликим струмком, а закінчується великою річкою.
Ч. К. Колтон
Добре усвідомлюю, що математиками всі учні не стануть. Як сільському вчителеві мені достатньо відомі та зрозумілі проблеми наших дітей та нашої школи. Адже підготовка дітей, а особливо їх всебічний розвиток, починається в сім’ї (та не завжди батьки мають змогу достатньо часу приділяти своїм дітям, а інколи вони їх взагалі не бачать інакшими, як мирно посопуючими в ліжку), продовжується в дитячому садочку, далі формується «фундамент математичної освіти» у 1-4 класах. Звичайно, зрозуміло, що подальше «виведення» стін «Храму математики» у 5-9 класах та «установка даху» у 10-11 класах передумовлена попередніми чинниками. Тому перш за все намагаюсь не втратити того
«потенційного матеріалу», що беру в руки у 5 класі.
«Будівництву» в розумі, душах дітей «Храму математики» були і будуть присвячені мої шкільні роки. Постійно всіма можливими та доступними способами від простого пояснення до переконання намагаюсь донести цю ідею до учнів та їх батьків.
Викладання мною математики базую на принципах:
-єдності зусиль учителя та учнів, їх батьків
-гуманізації навчального процесу
- демократизації стосунків між учителем та учнями - свідомої волі дітей та їх наполегливості у реалізації навчальної ідеї
- врахування результатів вивчення особистості учня, рівня їх задатків та знань під час організації
навчального процесу
- відбір оптимального змісту викладання -впровадження у процес викладання передових інноваційних технологій
- Значну увагу приділяю формуванню позитивної
мотивації роботи учнів на уроках
- форми та прийоми роботи на уроках: казка та її фрагменти, вірші-задачі, кросворди, математичне лото; ігри: «Сходинки», «До вершини знань», «Тут був Всезнайко», ребуси, ігри на відновлення записів тощо.
- колективна, групова, парна , індивідуальна форми роботи учнів та їх поєднання
- диференційований підхід до навчання учнів. - маю власну систему індивідуалізації завдань - Те, що я чую я забуваю.
Те, що я бачу й чую , я трохи пам’ятаю.
Те, що я бачу , чую, обговорюю я починаю розуміти.
Те, що я бачу , чую, обговорюю й роблю, я набуваю знань і навичок.
Математика цікава тоді, коли дає поживу нашій винахідливості й здатності до міркувань.
Д.Пойа
Виклад нового матеріалу супроводжую створенням проблемних запитань, задач та завдань. Нові факти встановлюються спільно, причинно-наслідкові висновки учні формулюють самостійно.
Роль на уроці звожу до ролі „Вчитель вчитися”.
Застосовую різноманітні інтерактивні форми та методи роботи з учнями: бесіди, ігри, нестандартні ситуації, самооцінка, самоаналіз, постановка особистих завдань учнями, самоаналіз рівня знань і умінь учнів на початку вивчення теми, а також в процесі вивчення нового матеріалу та вкінці вивчення теми.
Багато чого з математики не залишається в пам'яті, але коли зрозумієш її, тоді легко при нагоді згадати призабуте.
М. В. Остроградський
– розвиток творчих здібностей: виготовлення учнями кросвордів, ребусів, лото, ігор, написання казок, виготовлення стереометричних фігур та ін.
Предмет математики такий серйозний, що корисно не нехтувати нагодою робити його трохи цікавішим.
Б. Паскаль
- Повноцінне викладання математики неможливе без організації позакласної роботи з математики. Видається «Математична газета». Працює гурток «Юний математик». Проводяться предметні дні та тижні, в рамках яких проводились цікаві та змістовні заходи: «КВК», вечори «Математичні чудеса та таємниці», «Математиці присвячується»; ігри: «Брейн-ринг», «Щасливий випадок»,
«Що? Де? Коли?», «Турнір юних математиків»,
«Математична естафета» та інші.
Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер.
В. Сухомлинський
Індивідуалізуємо процес навчання
За час роботи у школі було випробувано багато різного: методик, форм та методів роботи з учнями, перегорнуто безліч сторінок різних збірників, методичної літератури, газених та журнальних статей. Та часто на уроках доводиться працювати не за сценарієм, а за обставинами, часто вигадуючи щось незвичне, нове. Я не претендую на геніальність та пожинання якихось лаврів, але, здається, я щось винайшов. Особисто мені це допомагає в роботі.
Я завжди маю можливість:
1) завантажити роботою кожного учня;
2) індивідуалізувати процес навчання;
3) є можливість реалізувати роботу в парах (сильніших учнів розсаджую із слабшими; вони справляються із завданням, як правило, раніше і потім консультують, допомагають та навчають своїх сусідів);
4) ці вправи можна застосовувати як тренувальні для закріплення вивченого матеріалу, так і для перевірки рівня сформованості знань, умінь та навичок учнів; 5) вправи можна використовувати на будь-якому етапі проведення уроку;
6) вправи можна використовувати при вивченні інших предметів;
7) вправи можна використовувати в різних класах.
Основна ідея така:
У шкільному курсі математики вивчається дуже багато формул, теорем. Як правило, вони містять змінні. Тому одній змінній можна присвоїти значення числа, що відповідає дню народження, другій присвоїти значення числа, що відповідає місяцю народження учня, третій – яку-небудь комбінацію з цих чисел або можна використати інші дати: день народження мами і т.д.
Наведу деякі приклади застосування методики індивідуальних завдань :
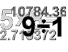
Під час вивчення алгебри:
1. Під час вивчення формул скороченого множення як тренувальні вправи, або перевірочні можна використати такі:
(а- n)2 = ; (c-n)(c+n)= ; (2m+5)2= ; (a+ n)3= .
n = числу, що відповідає числу дня народження учня, m = числу, що відповідає числу місяцю народження учня
2. Під час вивчення формули дискримінанта
2 + вх + с = 0 та його квадратного рівняння ах
знаходженні,
де:
а = числу, що відповідає числу дня народження учня, в = числу , що відповідає числу місяцю народження учня с= а+в чи якісь іншій комбінації.
3. Добре виправдало застосування цієї методики при вивченні властивостей степенів.
Наприклад:
а m . а n = ; (аm) n = ; аn :a m=
n = числу, що відповідає числу дня народження учня, m = числу , що відповідає числу місяця народження учня.
У процесі вивчення геометрії:
1. при вивченні суміжних та вертикальних кутів:
(знайти невідомий кут , чи кути (? ))
? m+350 ?
2) ?
m – числу , що відповідає числу місяцю народження учня.
2. при вивченні кутів, що утворюються при перетині двох прямих третьою:
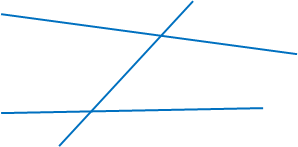
робота в парах: позначити один внутрішній односторонній кут (Д.н.+110)0 одного учня, а інший внутрішній
0 односторонній кут (30+Д.н.) другого учня. Знайти решту кутів (?).
? ?
?
(30+Д.н.)
? (Д.н.+110)0
? ?
3. при вивченні матеріалу про кути , що утворюються при перетині двох паралельних прямих січною:
b
?
a 2а0
Прямі a та b паралельні, 2а0= числу , що відповідає двом дням народження учня. Знайти невідомий кут (?) .
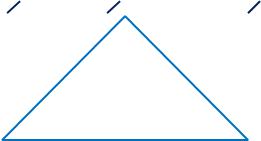
4. при вивченні суми кутів трикутника, чотирикутника, центральних та вписаних кутів
1) A = mo , B = no знайти C,
A
B C
n = числу, що відповідає числу дня народження учня, m = числу , що відповідає числу місяця народження учня.
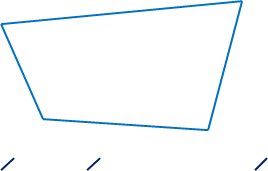B 2)
A
D
C
A = mo , B = no , C = mo+no , знайти D.
5. під час вивчення формул площ фігур
а) A B
D C
ABCD- квадрат , сторона рівна a см , SABCD-?
B C
|
|
б) b
A a D
ABCD- прямокутник, сторони рівніa смта b см, SABCD-?
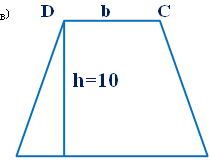
A а B ABCD- трапеція , сторони рівні a см та b см, SABCD-?
г) .О
На мал. коло з центром О радіусом r = a см S-?
6. Під час вивчення стереометрії (площі поверхонь та об’єми тіл)
.
R= n (см)
H=m+5 (см)
Знайти Sп.п. та V циліндра
(n = числу, що відповідає числу дня народження учня, m = числу , що відповідає числу місяця народження учня).
Це лише деякі приклади вправ, при мінімальній затраті фантазії їх може складати кожен. Перевага їх полягає в тому, що вони «народжуються» в голові , не потребують матеріальних затрат, дуже швидко наносяться на дошку класичним способом.
Урок геометрії у 7 класі
Тема уроку : Ознаки паралельності прямих Мета : Сформулювати ознаки паралельності прямих, вміти застосовувати їх для з’ясування, чи будуть прямі паралельними . Навчитись будувати паралельні прямі за допомогою лінійки та косинця з прямим кутом .
Формувати уміння доказово мислити та культуру математичної мови. Формувати уміння виконувати геометричні креслення.
Виховувати відповідальність та працьовитість.
Девіз уроку «Не махай на все рукою, не лінуйся, а учись,
бо, чого навчишся в школі, знадобиться ще колись!»
Хід уроку
1.Організаційна частина –(3 хв.)
-перевірка готовності до уроку ( зошити, книжки,
щоденники, креслярське приладдя) - наявність домашнього завдання
- створення позитивного настрою на урок
Гра «Талісман бажань»
(учні передають один одному кубик, виголошуючи при цьому слова-побажання на урок)
- побажання вчителя до уроку
Слайд 1.
3. Актуалізація опорних знань-(15 хв.)
«Мозковий штурм»
2) індивідуальні завдання (Д.н. - число, рівне дню народження учня)
? (40+Д.н.)0 ?
а) б) ? ?
- Гра «Невідомий гість» (Д.н.+100)0
3) робота в парах: позначити один внутрішній односторонній кут (Д.н.+110)0 одного учня, а інший внутрішній односторонній кут (30+Д.н.)0 другого учня. Знайти решту кутів.
? a ? (Д.н.+110)0
? (30+Д.н.)0 b ?
3) Гра «Невідомий гість» (учням пропонується ознайомитись із вмістом невідомого згортка, що залишив «Невідомий гість» , де на попередньо заготовлених малюнках навмисно переплутано кути, що кріпляться клейким папером та пропонується учням перевірити їх правильність і переставити паперові позначки кутів правильно)
Мал.1 Мал.2
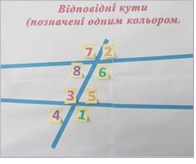
Мал.3
4) А тепер давайте ще раз подивимось, які кути утворяться, якшо дві різні прямі перетнути третьою.Демонстрація слайдів 2-5 (слайди анімовано для більшої наочності)
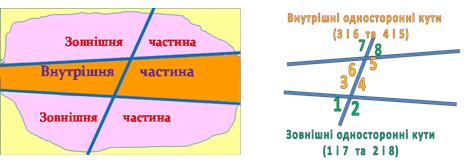
Слайд 2 Слайд 3
Слайд 4 Слайд 5 5) Які прямі називаються паралельними?
6) Назвіть найвдаліший приклад паралельних прямих (рейки на залізниці)
7) Скільки прямих, паралельних даній можна провести через точку? 8) Скільки прямих можна провести через 2 точки?
Довідка:Паралельний — від грецького «паралелой» — «ті, що йдуть поряд». Сучасний знак «||» використовується з XVIII ст., коли став загальновживаним знак рівності «=».
4. Мотивація навчальної діяльності учнів на уроці - (1 хв.)
- створення проблемної ситуації
(На дошці проводяться дві паралельні прямі. Учням ставляться запитання:
Як ви думаєте, які це прямі ? Чи можна якось перевірити, що вони паралельні?
Чи існують якісь математичні методи вирішення проблеми?
Гра «А поговорити…»
(учні висловлюють свої думки, вчитель підсумовує дискусію ).
-Так, є математичні методи вирішення цієї проблеми, а які вони,- про це ми і дізнаємось на сьогоднішньому уроці
5. Повідомлення теми та мети уроку -(1 хв.)
- Очікувані результати:
Сформулювати ознаки паралельності прямих, вміти застосовувати їх для вияснення, чи будуть прямі паралельними .
Навчитись будувати паралельні прямі за допомогою косинця з прямим кутом та лінійки.
Формувати уміння доказово мислити та культуру математичної мови.
Виховувати відповідальність та працьовитість. Формувати уміння виконувати геометричні креслення.
6. Реалізація мети та завдань уроку -(20 хв.) інтерактивна робота з учнями відповідно до теми
1)Формулювання та доведення ознак паралельності прямих.
Для підсумування етапу вивчення - демонстрація слайдів . Слайди 7-10 (слайди анімовано для більшої наочності)
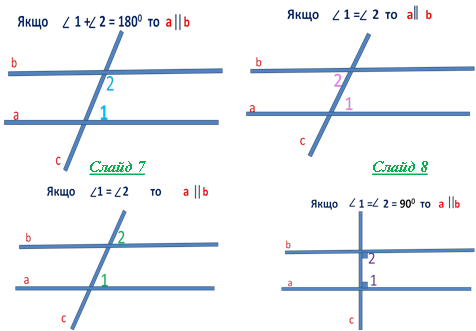Слайд 9 Слайд 10 2)-усне розв’язання задач № 1, 3, 6, 5, 7, 9 (за підручником).
Фізкультхвилинка (учні встають і за вказівкою вчителя демонструють кути) -(1 хв.)
3)-колективне розв’язування задачі (письмово) № 4, 11(3), 12(2) (за підручником ).
- диференціація завдань - 18(1) для сильніших учнів 4)-самостійне розв’язування № 13(2) (за підручником ), один учень виконує на відкидній дошці.
5) самоперевірка
7. Підведення підсумків уроку -(3 хв.) Гра «Мікрофон» Сьогодні на уроці я…
- задання д/з: параграф 8, № 13(1), 12(1),11(1,2), 15(1). творче завдання (кросворд,або лото) ,
коментар до нього
Слайд11.
- завершення уроку (подяка учням за урок)
Слайд12
Урок алгебри у 11 класі
Урок-гра «Експедиція до скарбниці знань»
(урок узагальнення та систематизації знань)
Узагальнення — це, мабуть, найлегший і найочевидніший шлях розширення математичних знань.
В. Сойер Тема уроку : Розв’язування показникових
рівнянь
Мета : систематизувати, узагальнити та поглибити знання і вміння учнів з теми; розвивати навички колективної та самостійної роботи; застосовувати вивчене до розв'язування завдань; виховувати увагу, старанність, культуру математичного мовлення.
Обладнання: картки із завданнями, заголовки до етапів гри, лото, таблиця узагальнення 1 (робоча по принципу лото) та 2 (та, що буде розміщена на дошці, великих розмірів аналогічна 1) , різнокольорові бонуси.
Девіз уроку : «Щоб дійти до мети, треба перш за все іти»
Бальзак
Хід уроку
1.Організаційна частина (1 хв.)
- створення позитивного настрою на урок
2. Мотивація навчальної діяльності учнів на уроці (2 хв.) -Показникові рівняння є однією із складових загальної математичної підготовки випускників. Вміння іх розв’язувати – крок до успіху як на випускних іспитах так і на ЗНО.
Тому зрозуміла важливість вашої роботи на уроці.
-оголошення гри
3.Реалізація завдань уроку
1 тур гри «Кодекс правил» Учні колективно складають таблицю відповідність запропонованих рівнянь (Таблиця 1)
|
Способи розв'язування показникових рівнянь |
Приклади рівнянь |
||
|
Найпростіші рівняння: |
|||
|
1 |
Зведення до однієї основи |
5x=25 |
|
|
|
Зведення до одного показника |
|
|
|
2 |
Врахування властивостей функції. |
4x = -16 |
|
|
Складніші рівняння: |
|||
|
1 |
Зведення до однієї основи, введення заміни (квадратні, алгебраїчні) ; |
9x+3х=18 ; |
|
|
2 |
Зведення до однакового показника та розв'язування однорідного рівняння першого степеня (ділення обох частин на степінь); |
|
|
|
3 |
Зведення до двох основ та розв'язування однорідного рівняння другого степеня (ділення обох частин на найвищу степінь); |
25х + 10х -2.4х =0 |
|
|
4 |
Винесення спільного множника за дужки та зведення до одного з по- передніх способів; |
4x+1+ 4x = 320 |
|
|
5 |
Графічний спосіб; |
|
|
|
6 |
Використання властивостей функцій; |
|
|
|
7 |
Використання декількох прийомів. Використання певних схем. |
( |
|
|
8 |
Штучні способи |
|
|
Учні отримують перший бонус зеленого кольору за 1 тур гри
2 тур гри «Початок подорожі» (лото)
Робота над завданням колективна.
Завдання : до умов зліва знайти правильну відповідь праворуч, учням видається для зразка складання ліва частина таблиці.
|
x Функція y=a при 0 <a<1 |
х=-1 |
|
x Функція y=a при 1 <a |
amn |
|
|
|
|
|
х=4 |
|
3х=81 |
Спадає на всій області визначення |
|
135х-4=-3 |
х=-2 |
|
|
х=-1,5 |
|
7х-2=1 |
х=1 |
|
|
Зростає на всій області визначення |
|
(0,2)х+1 = 0,04 |
х=2 |
|
(0,2)2х+2 = 5 |
|
|
|
Розв’язку немає |
(склавши лото і перевернувши листок учні отримують зображення метелика)
Вчитель: «Метелик – символ щастя.
Дуже багато рівнянь є в житті, .
Потрібно для кожного корінь знайти. Ви ж починаєте з парти шкільної, 3 пошуків «ікс» та задачі важкої! Раджу: хай труднощі вас не лякають,
Той переможе, хто їх подолає.
Р.Б. Аксельрод
Тож хай вам щастить в дорозі!»
Учні отримують другий бонус жовтого кольору за 2 тур гри.
3 тур гри «Без друзів ніяк...»
(Робота в парах, розв’язування рівнянь у зошитах, взаємоперевірка між парами)
1 пара 2пара
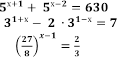
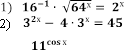3) = 121
Учні , отримують третій бонус синього кольору за правильність розв’язків 3 туру.
4 тур гри «Несподівані пригоди»
( Диференційовані індивідуальні завдання підвищеного рівня складності ( учням пропонується вибрати картку з рівняннями підвищеного рівня складності. Учні вибирають собі рівняння, встановлюють його тип та розв’язують біля дошки )
1. 
2. 
(
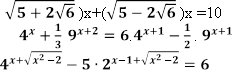3. 3 .
4.
Учні отримують четвертий бонус червоного кольору за правильне розв’язання завдань 4 туру.
5 тур гри «Найсильніший гравець»
З учнями проводиться бесіда з метою визначення найкращого (на їх погляд гравця) і за її результатами та висновками і пропозиціям вчителя найсильнішому гравцю вручається бонус малинового кольору та відповідно 1 бал до оцінки під час проведення підсумків уроку.
6 тур гри «Відкрий свою скарбницю»
(Підведення підсумку уроку: оцінювання ( зелений бонус 4 -5 балів; зелений та жовтий 6-7 балів; зелений, жовтий та синій бонуси 9-10 балів; зелений, жовтий, синій та червоний бонуси 10-11 балів; враховується рівень участі у виконанні завдань, активність тощо), задання домашнього завдання )
Домашнє завдання
Рівень А)
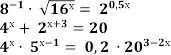1)
2)
3)
4) 25х + 10х -2.4х =0
Рівень Б)
(розв’язати ті рівняння, які не виконувались учнем у класі з 1-4)
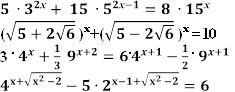
Зразок бонусів:
|
18.11.2011 |
18.11.2011 |
|
18.11.2011 |
18.11.2011 |
|
18.11.2011 |
18.11.2011 |
Позакласна робота з математики
- На одній із шкільних лінійок попередньо оголошується, що незабаром у школі проводитиметься
ТИЖДЕНЬ
МАТЕМАТИКИ.
Мета такого анонсування – підготовка учнів до тих заходів, що проводитимуться протягом тижня.
-Напередодні проведення тижня математики, або ж у понеділок до початку занять у вестибюлі школи розміщується велике і красиве оголошення. У ньому розписано по днях заходи, що проводитимуться у рамках проведення тижня. Наведені деякі вислови про математику, ілюстровано тематичними малюнками. Одного разу „Тиждень математики” проводився згідно такого плану:
Понеділок.
Відкриття „Тижня математики” (на лінійці оголошується план проведення тижня, ставляться завдання та проводиться „Мініконцерт”
„Цариці-математиці надсилаємо вітання”)
Вівторок.
Конкурс художників (математично-геометричні фантазії учнів – малюнки виконуються за допомогою геометричних фігур, або цифр).
Середа. „Турнір юних математиків”
(6-7 класи)
Четвер. Конкурс кросвордів та ребусів на математичну тематику.
П’ятниця.
КВК „Цариці математиці присвячується !”
Протягом тижня відбувається підведення підсумків конкурсу „Ерудити, вперед” (3-11 класи; завдання конкурсу були розміщені у шкільній „Математичній газеті” на початку II семестру, завдання різновікові )
Остаточне підведення підсумків проводиться на одній із наступних шкільних лінійок.
„ЦАРИЦІ МАТЕМАТИЦІ ПРИСВЯЧУЄТЬСЯ”
К В К для 8-11 класів
(у грі беруть участь дві команди:
збірна 8, 11 класу та збірна 9,10 класу)
Програма проведення КВК:
1. Представлення команд (назва, девіз, емблема, вітання уболівальникам, жюрі, супернику та інше)
(оцінка від 1 до 5 балів, журі виставляє бали, рахується середній бал ).
2. Конкурс „Розминка” (за кожну правильну відповідь 0,1 бала)
3. Конкурс „Математичний олімп” (за кожну правильну відповідь 0,1 бала)
4. Конкурс „Найсильніша фігура” (команди представляють рекламу кулі та циліндра, жеребкування і підготовка завчасна) (оцінка від 1 до 5 балів, журі виставляє бали, рахується середній бал ).
5. Конкурс художників „Математично-геометричні фантазії” (командам було задано завдання зообразити Зайця та Вовка з мультика „Ну постривай!” за 3 хв. за допомогою геометричних фігур). (оцінка від 1 до 4 балів, журі виставляє бали, рахується середній бал ).
6. Конкурс „Вірю, не вірю”(за кожну правильну відповідь 0,1 бала)
7. Музичний конкурс „Серенада математиці” (це домашнє завдання, команди співають, жартують, інсценують, танцюють на тему „ Математика навколо нас» (оцінка від 1 до 5 балів, журі виставляє бали, рахується середній бал
).
8. Підведення підсумків гри.
Додатки до КВК:
Конкурс капітанів
1.Що спільного мають відоме дерево баобаб і підручник
„Алгебра”? (корінь)
2.Горіло 5 свічок, 3 потухло . Скільки залишилось свічок ?
(три)
3.Чи можна замість крапок підібрати такі цифри, щоб число
.....08 було точним квадратом ? (ні)
4.Скільки трикутників зображено на малюнку ? (13)
5.З Києва до Львова вирушив поїзд із швидкістю 60 км/год, а із Львова до Києва із швидкістю 70 км/год.Який з поїздів буде далі від Києва в момент зустрічі? ( будуть на однаковій відстані)
Розминка
1.Підрахувати скільки ударів за добу зробить годинник з боєм, який відбиває від 1 до 12 ударів на кожну годину.
(156)
2.Скажіть точно, коли почалося XXI століття. (01.01.2001
року після 0 годин)
3.Число 666 збільшити у півтора рази не виконуючи над ним ніяких дій. (999)
4.Запишіть найбільше число за допомогою чотирьох одиниць не вживаючи знаки математичних дій.
(1111)
5.Чи є тупокутним трикутник з сторонами 7м, 9м та 18м ?
(такого трикутника не існує
Математичний олімп
1.Допоможіть будь-ласка підрахувати шевцю: через скільки днів він відріже останній кусок матерії, якщо він має 16 м матерії і щодня відрізає по 2 метри. (7)
2.У кружечках розмістити числа від 1 до 6 так, щоб на кожній стороні трикутника були однакові суми.
3.Користуючись лише додаванням записати число 28 за допомогою 5 двійок і знака арифметичної дії додавання. (2+2+2+22)
4.У скільки раз sin58° більший за cos58°. (у tg 580 ) 5.Двоє друзів підійшли до річки на березі якої стояв човен, який може перевозити лише одного. І все таки друзям вдалося переправитися на другий берег. Я це їм вдалося?.
(підійшли з різних берегів)
6. Відгадайте, що означає у цифрах запис чай : ай =5?
(125:25=5)
7. Назвіть математика, який не любив розв’язувати квадратні рівняння за допомогою дискримінанта.
(Ф.Вієт)
8. Без чого не може обійтися математик барабанщик і мисливець? (дробу)
9. Скільки граней має новий шестигранний олівець? (8) 10. Чи можуть бісектриси трикутника перетинатись під прямим кутом? (ні)
Вiрю не вірю
1. Чи вiриш ти, що в основi всiх сучасних пiдручникiв з геометрii лежать знаменитi «Начала» Евклiда, написанi в I столiтгi до н.е.? (Так)
2.Чи вiриш ти, що великий М.Ю. Лермонтов захоплювався математикою і мiг до пiзньої ночі розв’язувати яку-небудь математичну задачу? (так, товариш Лермонтова Лопухiн писав про це)
3. Чи вiриш ти, що вiрш «О сколько нам открытий чудных…» написав М.Ю. Лермонтов?
(Нi. О.С. Пушкiн)
4.Чи вiриш ти, що Пiфагор брав участь в кулачних боях на 58 Олiмпiадi, яка проходила в 548 роцi до н.е.?
(так, він був чемпiоном з цього виду спорту i виборював цей титул ще на декiлькох олiмпiадах)
5. Чи вiриш ти, що Шарль П’єрро, автор «Червоної
Шапочки”, написав казку «Кохання циркуля та Лінійки”?
(Так, така казка є)
6.Чи вiриш, що Наполеон Бонапарт писав математичнi роботи?
(Так, один геометричний факт несе назву «Задача
Наполеона»)
7. Чи вiриш ти, що О.С. Пушкiн написав рядки «Вдохновение нужно в геометрии, как и в поэзии»? (Так)
8. Чи вiриш ти, що вiдомий Фалес був болiльником та помер на трибунi Олiмпiйського стадiону пiд час бою Пiфагора?
(Так. На 58 Олiмпiадi)
9. Чи вiриш ти, що якщо кожен день по десять годин тiльки переписувати працi Леонарда Ейлера, не вистачить і 75 рокiв?
(Так, зібрання його творiв дуже велике - 75 томів)
10. Чи вiриш ти, що Л.М.Толстой написав підручник для початкової школи ? (так)
11. Чи вірите ви, що Нобелівська премія не присуджується за досягнення в галузі математики ?
(так, бо жінка Нобеля зрадила і втекла з математиком) 12. Чи вірите ви, що математику у нашій школі на сьогоднішній день читає 7 вчителів ? (так, якщо рахувати вчителів початкових класів)
«Математичні чудеса та таємниці»
Вечір відпочинку для старшокласників
( Вечір відбувається в залі прикрашеній висловами про
математику, математичними стінгазетами. Учасникам вечора заздалегідь пропонують взяти з собою листки паперу, ручки, калькулятори)
Вступне слово вчителя. Шановні присутні ! Ми раді вітати вас на нашому незвичайному вечорі. Саме так - сьогодні він незвичайний. Бо, на відміну від уроків, де вам доводилось рахувати, напружено думати, розв’язувати різні вправи та задачі, ви станете сьогодні свідками справжніх чудес. Тож дозвольте побажати вам незабутніх вражень та вдалої подорожі в країну «Математичних чудес та таємниць».
Група старшокласників наполегливо готувалася до сьогоднішнього вечора. Тож надаємо їм слово.
(Далі по черзі старшокласники – чародії демонструють глядачам свої фокуси, описи яких додаються)
Фокус №1
Таємнича дев'ятка
Обладнання: похилий стіл, покритий темною тканиною з негладкою поверхнею , білі монети (5- ти копієчні) 25-30 штук.
Дюжина (чи більше) монет розміщається на столі у формі дев'ятки (мал. 1). Демонструючий стоїть, повернувши спиною до глядачів. Хто-небудь із присутніх задумує число, більше числа монет у "ніжці" дев'ятки, і починає відраховувати монети знизу нагору по ніжці і, далі, по колечку проти годинної стрілки, поки не дійде до задуманого числа. Потім він знову рахує від одиниці до задуманого числа, почавши з монети, на якій зупинився, але цього разу по годинній стрілці і тільки навколо колечка.Під монету, на якій закінчився рахунок, ховається маленький шматочок папірця. Демонструючий повертається до столу і відразу ж піднімає цю монету.
Пояснення. Незалежно від того, яке число було задумано,
рахунок закінчується завжди на одній і тій же монеті ). Спочатку самі проробіть усе це в розумі з будь-яким числом, щоб довідатися, яка це буде монета. При повторенні фокуса додайте до ніжки кілька монет, тоді рахунок закінчиться вже в іншім місці.
Мал. 1
Рахунок закінчується завжди у кожному випадку на позначеном у кружечку не залежно від числа, що відповідає умові фокусу.
Фокус №2
Таємничі квадрати
Обладнання: демонстраційна дошка, настінний помісячний календар з досить великими цифрами, маркер.
Демонструючий стоїть , повернувшись спиною до глядачів, а один з них вибирає на помісячному табель-календарі будьякий місяць і відзначає на ньому який-небудь квадрат, що містить 9 чисел. Тепер досить глядачу назвати найменше з них, щоб демонструючий відразу, після швидкого підрахунку, оголосив суму цих дев'яти чисел,
Пояснення. Демонструючому потрібно додати до названого числа 8 і результат помножити на 9 .
Далі глядачам пропонуються ряд фокусів з картами, причому останні послуговують як об’екти, що служать для рахування, або такі що мають певні властивості по кольору.
Фокус №3
"Манхеттенські чудеса"
Обладнання: колода гральних карт
Глядача просять зняти колоду приблизно посередині, узявши собі будь-яку половину і перерахувати в ній карти. Допустимо, їх 24. Два плюс чотири дає шість . Глядач запам’ятовує в своїй півколоді шосту карту знизу, кладе цю напівколоїду на іншу і, підрівнявши карти, вручає їх демонструючому. Останній починає здавати карти по одній на стіл, вимовляючи при цьому по-буквенно фразу "М-а-н-хе-т-т-е-н-с-ь-к-і-ч-у-д-е-с-а", причому так, щоб на кожну покладену карту приходилося по одній букві. Разом з останньою буквою з'явиться замічена карта.
Пояснення.У результаті описаної процедури обрана карта завжди виявляється на дев'ятнадцятому місці зверху. Тому будь-яка дев'ятнадцятибуквена фраза приводить до потрібної карти.
Фокус №4
Фокус з королями і дамами
Обладнання: колода гральних карт
З колоди вибирають королів і дам і розкладають їх на дві купки: королі окремо, дами окремо. Купки перевертають лицьовою стороною вниз і укладають одна на іншу. Глядача просять "зняти" нашу колоду з восьми карт один чи кілька разів. Демонструючий забирає купку за спину і відразу відкриває перед глядачами дві карти. Виявляється, що це король і дама однієї масті. З іншими трьома парами можна продемонструвати теж саме.
Пояснення.. Демонструючому варто подбати лише про те, щоб у двох початкових купках послідовність мастей була однаковою. "Зняття" цієї послідовності не порушить. За спиною демонструючий тільки розділяє купку строго навпіл і одержує потрібні пари, беручи в кожній половині верхню карту. У цій парі завжди виявляться король і дама однакової масті.
Фокус №5
Зіставлення числа карт чорної і червоної масті Обладнання: колода гральних карт
З колоди вибирають десять карт: п'ять червоних і п'ять чорних. Карти якого-небудь одного кольору перевертаются, і всі десять карт ретельно тасуються глядачем. На мить демонструючий забирає карти за спину. Потім він протягає руки вперед, тримаючи в кожній з них по п'ять карт які відразу розкладаються на столі. Число відкритих карт у кожній п'ятірці виявляється однаковим, і ці карти будуть різного кольору. Наприклад, якщо в одній п’ятірці виявляться три червоні карти, то в іншій п’ятірці будуть відкритими три чорні карти. Фокус можна повторювати скільки завгодно разів,і він буде завжди вдаватися.
Пояснення. Неважко зміркувати, що серед карт однієї п'ятірки буде відкритих карт (а вони одного кольору, наприклад чорного) стільки ж, скільки закритих (червоних) в іншій п'ятірці. За спиною варто просто розділити пачку навпіл і, перш ніж показати карти глядачам, перевернути одну з половин. Таким чином, завдяки тому, що карти перевернуті, число відкритих карт у кожній п'ятірці буде однаковим і ці карти будуть різного кольору. У цьому фокусі, звичайно, можна скористатися будь-яким парним числом карт, потрібно тільки, щоб половина їх була червоною, а половина-чорною.
Фокус №6
Угадування задуманного числа на циферблаті Обладнання:годинник з циферблатом, указка.
Глядач задумує яке-небудь число від 1 до 12. Демонструючий починає доторкатися кінчиком указки до чисел на циферблаті, роблячи це, очевидно, у зовсім довільному порядку. У цей час глядач рахує про себе, починаючи з задуманого числа до двадцяти, причому так, щоб на кожний дотик припадало одне число. Дорахувавши до 20, він говорить «Стоп» . І (дивне співпадіння) указка в цей момент знаходитиметься на задумному числі.
Пояснення. Перші вісім доторкань дійсно робляться зовсім навмання. Однак уже на дев'ятому демонструючий повинний обов'язково торкнутися 12 і з цього моменту перебирати годинник строго підряд у напрямку, зворотному руху годинної стрілки. Коли глядач вимовить слово "стоп", указка буде показувати на задумане число.
Зовсім не обов'язково просити глядача припиняти рахунок саме на 20, ви можете запропонувати йому самому вибрати число для закінчення рахунку: потрібно лише, щоб воно було більше 12. Звичайно, глядач повинний попередити вас, на якім числі він планує зупинитися. Відніміть від цього числа 12, отриманий залишок укаже, скільки доторкань потрібно зробити навманя, перш ніж доторкнутися до 12 і почати рухатися послідовно проти годинної стрілки.
Фокус №7
Хто що взяв?
Обладнання: коробка сірників, ложка, вилка, ніж. Ще один стародавній фокус можна показати на 24 сірниках, що складаються купкою поруч із трьома невеликими предметами, скажемо, ложкою, виделкою, ножем. У фокусі просять взяти участь трьох глядачів (будемо називати їх умовно 1,2,3). Перший глядач одержує один сірник, другийдва, третій-три. Демонструючий повертається до них спиною і просить кожного взяти по одному з лежачих на столі предметів (позначимо їх ній Л,В та Н).
Тепер глядачу, що тримає предмет Л, пропонується узяти рівно стільки сірників з числа залишившихся в купці, скільки в нього на руках. Глядач, що взяв В, нехай візьме двічі стільки сірників скільки в нього на руках. Останньому глядачу, що взяв предмет Н, запропонуєте взяти чотирижди стільки сірників, скільки в нього на руках. Після цього нехай усі три глядачі покладуть свої предмети і сірники в кишені. Обернувшись до глядачів і глянувши на сірники, що залишилися, ви відразу ж говорите кожному глядачу, який предмет він узяв.
Пояснення. Якщо залишається один сірник, то глядачі 1, 2 і
3 узяли відповідно предмети Л,В і Н (саме в такому порядку).
Якщо залишилося 2 сірники, то порядок предметів буде В, Л, Н. Якщо залишилося 3 сірники , то Л, Н, В.Якщо 4 сірники, то хтось помилився, тому, що подібний залишок неможливий.
Якщо 5, то порядок предметів буде В, Н, Л. Якщо 6, т о Н, Л, В. Якщо 7, то Н, В, Л. Зручною буде така схема 1 - ЛиВеНь. 2 - ВоЛаН
3 - ЛіНиВець.
5 - ВаНіЛь.
6 - НеВоЛя.
7 - НаЛиВка
Тут буква "Л" повинна позначати ложку, "В"-вилку, "Н"- ніж. Букви розташовані в словах у порядку, що відповідає порядку предметів. Числа перед словами, позначають число сірників, що залишилися.
Фокус №8
Фокус з шістьма квадратами
Обладнання: шість квадратних пластинок, пофарбованих у різні кольори.
Це фокус, в якому дотик до предмета указки супроводжується побуквеною вимовою чисел.
червоний жовтий голубий
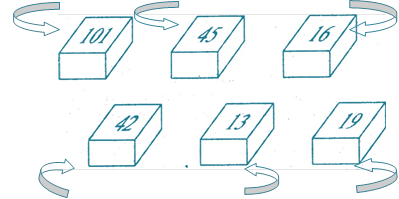оранжевий зелений синій
Мал.2
Для показу фокусу потрібно шість квадратних пластинок,
пофарбованих у різні кольори. На кожній пластинці зображене число. Пластинки розкладають на столі числами вниз. Фокусник відвертається, а глядач у цей час піднімає одну з пластинок, дивиться на число, а потім змішує її з рештою. Тепер фокусник повертається до столу і починає торкатися указкою до пластинок. Глядач у цей час вимовляє про себе побуквено своє число так, щоб на кожний дотик припадало по одній букві. Коли всі букви числа будуть вичерпані, глядач говорить «стоп». Пластинка, на якій зупинилась указка, перевертається, причому виявляється, що на ній якраз і намальовано задумане число.
Пояснення. Перші шість дотиків робляться довільно.
Наступні шість у такій послідовності: 101, 42, 45, 13, 16, 19. Для цього треба запам'ятати кольори, яким відповідають ці числа (можна скористатись відомою лічилкою кольорів веселки «Каждый охотник желает знать ,где сидять фазаны». Перші букви слів лічилки вказують назви кольорів російською мовою, звичайно ж фіолетовий у фокусі не задіяний). Фокус обумовлений тим, що запис числа 101 (сто один) містить сім букв, а кожного наступного — на одну букву більше
Фокус №9 
Карта квітів
Обладнання:карта квітів (малюнок 3) Існує багато й інших фокусів, у яких застосовується принцип побуквенного вимови слів. Така, наприклад, "карта квітів". Лицьова її
сторона представлена на мал.3. Глядач задумує квітку, хто показує починає перебирати олівцем отвори. При кожнім дотику глядач називає про себе одну букву з назви обраної квітки і вимовляє уголос: "стоп", коли його слово буде вичерпано. Олівець вставляється в останній задіяний отвір, і карта перевертається. Вістря його буде висуватися саме там, де надрукована назва задуманої квітки.
Пояснення. Перший дотик робиться у верхнього отвору, далі отвори обходяться через одне по годинній стрілці.
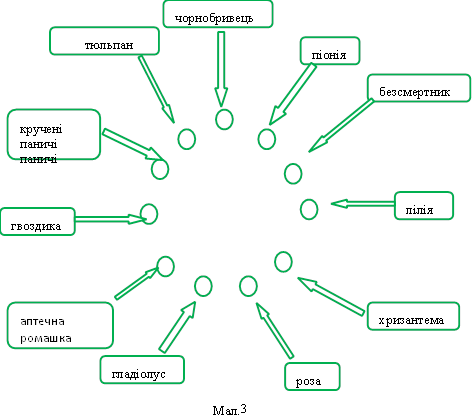
Фокус №10
Задумай тварину
Обладнання:карта звірів (малюнок 4)
Фокус-картинка, схожа на тільки що описану "карту квітів", зображена на мал. 4. Глядач задумує яку-небудь тварину, зображену на малюнку і вимовляє про себе назву його по буквам, в той час як показуючий торкається до малюнків.
Почавши з гіпопотама, він переходить потім нагору по лінії до тигренятка і так продовжує обхід усіх тварин, рухаючись в напрямках, що вказуються лініями, поки глядач не дійде до останньої букви свого слова і не скаже "стоп".
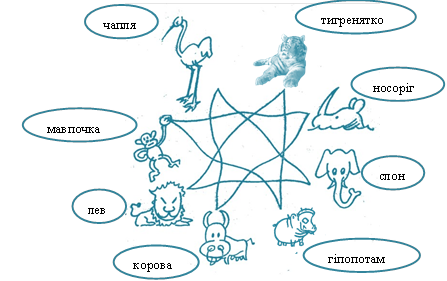
Мал.4
Фокус №11
Додавання чисел Фібоначчі Обладнання:дошка, крейда.
Числами Фібоначчі називають ряд чисел, у якому кожне, починаючи з третього, являє собою суму двох попередніх.
Цей фокус демонструють так:хто показує просить когонебудь записати одне під другим два будь-яких числа, які він побажає. Допустимо для приклада, були обрані 8 і 5. Потім глядач повинний додати ці числа. Знайдене в такий спосіб третє число додається з другим ( що стоїть над ним), і виходить четверте число. Цей процес повторюють доти, поки у вертикальному стовпці не виявиться десять чисел:
8
5
13
18
31
49
80
129
209
338
Під час записування чисел демонструючий стоїть, повернувши спиною до глядачів. Коли всі числа будуть записані, він повертається, проводить під стовпчиком цифр риску і, не задумуючись, підписує суму цих чисел. Щоб одержати цю суму, йому просто потрібно взяти четверте число знизу і помножити його на 11-операція, яку легко можна проробити в розумі). У нашому випадку четвертим числом буде 80, тому у відповіді вийде число 80, узяте 11 разів, тобто 880.
Фокус №12
Таємниця дев'ятки
Обладнання: дошка, крейда,картка з числом 1089.
Написавши в зворотному порядку будь-яке тризначне число (при умові, що перша й остання його цифри різні) і віднявши від більшого числа менше, ми завжди одержимо в середині дев'ятку і суму крайніх цифр, теж рівну 9. Це означає, що ви відразу можете назвати результат віднімання, знаючи тільки його першу чи тільки останню цифру. Якщо тепер написати різницю в зворотному порядку і ці два числа додати, то вийде 1089. Число 1089 пишеться заздалегідь на листку паперу, що потім перевертається лицьовою стороною вниз. Після того як глядач закінчить серію операцій, описаних вище, і оголосить свій остаточний результатам 1089, покажіть записане вами пророкування, тримаючи при цьому лист вгору ногами. Написане на ньому число буде прочитано як 6801, що, звичайно, не буде правильною відповіддю. Зробіть здивоване обличчя, а потім вибачтесь, що взяли лист не так, як потрібно. Поверніть його на 180° і покажіть вірне число. Ця невелика вистава вносить розважальний момент у демонстрацію фокусу.
Фокус №13 Відгадування віку Обладнання: дошка, крейда.
Цікавий спосіб відгадування віку деякої особи (це може бути хтось з батьків чи гостей вечора) починається з того, що його просять виконати ряд яких-небудь дій, що приводять до числа, що має своїм своїм цифровим коренем дев'ятку (достатньо помножити на 9 результат будь-яких попередніх дій з будь-якими числами). Потім пропонують додати до отриманого числа свій вік і повідомити вам суму. По цій сумі легко довідатися вік глядача. Спочатку знайдіть цифровий корінь суми (якщо скласти всі цифри деякого числа, потім всі цифри тільки що знайденої суми і так продовжувати до тих пір поки вийде одноцифрове число, яке і має назву цифровий корінь початкового числа). Потім додавайте до нього дев'ятки до тих пір, поки отримане число на покажеться вам найбільш близьким до віку вашого співрозмовника. Це число і буде шуканим віком. Наприклад ви попросили глядача написати будь-яке число і помножити його на 9, після чого в нього вийшло 2826. До цього числа він додав 40, свій вік, і повідомив вам суму: 2866. Цифровий корінь цього числа дорівнює 4( 2+8+6+6=22, 2+2=4) ; додаючи до четвірки дев'ятки, одержимо числа 13, 22, 31, 40, 49 і т.д. , оскільки з точністю до 9 років оцінити вік неважко, ви встановлюєте, що правильною відповіддю буде 40.
Якщо скласти всі цифри деякого числа, потім всі цифри тільки що знайденої суми і так продовжувати до тих пір поки вийде одноцифрове число, яке і має назву цифровий корінь початкового числа.
Фокус №14
Швидке добування кубічного кореня Обладнання: дошка, крейда, калькулятор для глядача. Демонстрація фокусу з добуванням кубічного кореня починається з того, що кого-небудь із присутніх просять узяти будь-яке число від 1 до 100, піднести його до кубу і повідомити вголос результат. Після цього демонструючий миттєво називає кубічний корінь з названого числа. Для того щоб показувати цей фокус, потрібно спочатку вивчити куби чисел від 1 до 10:
При вивченні цієї таблиці виявляється, що всі цифри, на які закінчуються куби, різні, причому у всіх випадках, за винятком 2 і 3, а також 7 і 8, остання цифра куба збігається з числом, що підноситься до кубу. У виняткових же випадках остання цифра кубу дорівнює різниці між 10 і числом, що підноситься до кубу.
Наприклад: нехай глядач, підносячи деяке число до кубу, одержав, наприклад, 250 047. Остання цифра цього числа 7, з чого негайно випливає, що останньою цифрою кубічного кореня повинна бути 3. Першу цифру кубічного кореня знаходимо в такий спосіб. Закреслимо останні три цифри кубу (незалежно від кількості його цифр) і розглянемо цифри, що стоять попереду,- у нашому випадку це 250. Число 250 розташовується в таблиці кубів між кубами шістки і сімки. Менша з цих цифр - у нашому випадку 6 - і буде першою цифрою кубічного кореня. Тому правильною відповіддю буде
63.
Щоб краще усвідомити суть справи, приведемо ще один приклад. Нехай назване число 19 683. Його стання цифра 3 указує, що останньою цифрою кубічного кореня буде 7. Закреслюючи останні три цифри, одержуємо число 19, що лежить між кубом двійки і кубом трійки. Меншим з цих чисел буде 2, тому шуканим кубічним коренем буде 27. Може здатися дивним , але для добування цілочислених коренів зі степенів більш високих, чим третя, існують більш прості правила. Особливо легко знаходити корені п'ятого степеня, тому що будь-яке число і його п'ятий степінь завжди закінчуються однієї і тією же цифрою.
Фокус №15
"Психологічні моменти"
Ще одна категорія фокусів з числами, зовсім відмінна від фокусів з пророкуванням чи відгадуваннямм числа, заснована на тім, що називають психологічними моментами. Ці фокуси не завжди получаются, але по якихось невідомих причинах психологічного характеру шанси на успіх при їхній демонстрації виявляються значно більшими, ніж цього можна було очікувати. От простий приклад. Якщо ви попросите назвати яке-небудь число від 1 до 10, більшість людей назве сімку, а якщо задані границі будуть 1 і 5, то - трійку. Ще один цікавий психологічний фактор, невідомо ким уперше помічений, можна використовувати у фокусі в такий спосіб. Напишіть на клаптику паперу число 37 і відкладіть його убік , Потім, звертаючи до присутніх, скажіть: "Напишіть, будь ласка, двозначне число між 1 і 50, щоб обидві його цифри були непарними і різними. Наприклад, число 11 писати не можна". Може показатися дивним, але багато шансів, що більшість глядачів напишуть 37 (друге найбільш ймовірне число 35). По суті, їх вибір обмежений вісьма числами, причому згадування числа 11 як би залучає їх мислення до чисел третього десятка. Якщо цей фокус у вас вийде, спробуйте за ним інший. Цього разу попросіть написати двозначне число між 50 і 100, обидві цифри якого повинні бути парними і, як і в попередньому випадку, різними. У даному випадку вибір глядача обмежений сьома числами, з яких начебто частіше усіх називають 68. Якщо під руками маються гральні карти, можна пророчити це число, поклавши на стіл шістку і вісімку лицьовою стороною вниз. Це підвищує ваші шанси на успіх, тому що ви маєте вибір між двома можливими відповідями, тобто між 68 і 86, у залежності від того, яку карту ви відкриєте першою.
Заключне слово вчителя. .
Шановні присутні!
От і перегорнута остання сторінка нашого незвичного математичного вечора.
Сьогодні ви відкрили для себе математику з іншої сторони, стали свідками і учасниками справжніх чудес.
Це лише маленька часточка того, що може творити математика.
Я запрошую вийти до глядачів наших чародіїв.
Давайте ще раз подякуємо їм оплесками за проявлені вміння, артистизм та наполегливу підготовку
Тож гортайте книги, знаходьте нове для себе, підкоряйте таїни і спішіть порадувати нас своїми новими відкриттями.
Спасибі за увагу та участь.
До нових зустрічей!
Математичний міні-концерт
(концерт відбувається під час презентації тижня математики)
(місце проведення – відповідно оформлені шкільна лінійка, клас, зала, тощо) Учень 1:
Сьогоднi будем, друзi, з вами Царицю всiх наук вiтать. Так можем гордо i по праву Науку цю ми величать.
Учень 2:
Щоб концерт наш розпочати
Загадку треба відгадати
Наук цариця недосяжна — Могутня, щедра і прекрасна — Блискуче розум розвиває, Правильно мислити всіх навчає. Неперевершена її краса, Чудова логіка, струнка. Скажiть - но, друзі, хто вона така...
ЦЕ …(математика)
(виходить „Цариця-математика у відповідному вбранні)
Учень 3: (звертається до «Цариці-математики») Ти визнана давно главою всіх наук
Потрібна нам ти завжди, скрізь i всюди. Без математики ми нинi, як без рук:
З тобою з казки дiйснiсть творять люди.
Учень 4:
Освоївши тебе, рвемося у полiт,
Створили ми розумнi вже машини, Штурмуємо космiчний світ
I рiзних фактів узнаєм причини.
Учень 5:
З тобою ми невпинно ростемо, З тобою пiдкоряємо природу. Твої досягнення ми вiддамо
На благо українського народу.
Пісня про математику
(виконує група учнів)
Сила точної науки, Що створив наш генiй, дала зброю людям в руки
В працi їх щоденнiй.
Приспів:
Найдавнiша на планетi
Між наук цариця, — Математика — ти наша Вiрна помiчниця.
Чи будинок зводим друже друже,
Чи пливем морями, — Скрiзь вона тобi послужить,
Всюди вона з нами.
Приспiв:
На заводі і в друкарні
В вiдкритях галактик, Навіть лiкар у лiкарнi
Мусить її знати.
Приспiв:
Далі виконуються гуморески:
Читець 1.
Батько глянув у щоденник i питає сина: -
Грицю, це ж за що тобi учитель влiпив одиницю? Гриць знiтився i промимрив так, що ледве чути, „Та... то я... не мiг сьогоднi кореня добути».
Ой лелечко! Чи ви чули? — обурилась мати.
- Вже дитину заставляють коренi тягати!
Читець 2.
Викликас вчитель Люду,
Слабку серед дiтвори, I питає: Скiльки буде: десять падiлить на три ? Роэв ‘язать вона не може, Звiсно, знітилась, мовчить... Вчитель каже: Так не гоже, Простi дроби треба вчить. Хай картоплi є десяток, Вчитель далi рiч веде. — Розділи на трьох дiвчаток, То по скiльки припаде? Люда каже: Зайвий клопiт, i нащо менi це знать?
Я зварю їм ту картоплю,
Потовчу, і хай їдять...
Група учнів виконує частівки:
Ми веселi двi подружки iз баяном-братиком Заспiваємо частушки Вам про математику.
Знають Ігор, Коля й Вася:
Залiк наближаеться,
А в них з алгебри у зошит Рiвень понижаеться.
Отака в усiх нас доля
Залiки — страждання: Не дає списати вчитель З алгебри завдання.
Розв ‘язав Петрусь задачу,
Тiльки мінуса не бачив,
От i сталось, що лимон
— Важить майже вісім тон
На контрольній ловив гав,
Нижчий рiвень упiймав,
Пiдглядав в усi книжки, Переплутав сторiнки. Бiля дошки він стояв i придумав чудо В теоремi прирiвняв до квадрата куба.
Хто задач не полюбляє,
Тим така i дяка — З низьким рiвнем у знаннях Й вийде лобуряка.
(сценка за участю учня та Цариці- математики)
Учень:
Нестандартні, цiкаві задачі Я б розв‘язував ночi і днi. А мене лиш чекають невдачi, Не щастить в цій науцi мені.
Цариця-математика: Скільки чашок, скільки ложок — Це ж простеньке завдання. Ти додав слонів до кішок, Перемножив на коня. Справді, нескладна наука — Була б відповідь як слід! Вийшло: дід молодший внука Аж на 49 літ! А друкарські дві машини Косять жито 8 днів. Проїжджають щохвилини Три десятих поїздів. А до Марса — метрів 300 (мудра в хлопця голова!). Пів хлоп'яти їде в місто, З ним —пів мами.
Ну й дива!
Учень:
Хоч сідай і гірко плач — Не люблю отих задач! Ох! Замучили задачі, Через них одні невдачі. Чи підручники погані,
Чи такий я безталанний? Та усіх я обдурю—
В книжці відповідь знайду!
Цариця-математика:
Будеш, друже, трудитись сумлінно —
У навчаннi уникнеш невдач,
I розв ‘яжеш на добре й вiдмiнно Не десяток, а сотні задач.
Учень 1:
Глибина і абстракцii сила, Підрахунок в задачі стрункий. Строга логіка, виклад красивий,
Математиків ваблять віки.
Учень 3. Є наука, що розум приводить
У порядок ясний і чіткий, Нам вона теореми доводить, Що поєднують формул рядки. Математику всі ви впізнали,
Від людей всіх їй честь і хвала, Також всім, хто її підкоряли, Промовляєм подяки слова.
Учень 2:
Проникаючи в зорянi далі, В таємниці земної кори, Математика всіх закликас:
(разом
Ти мiркуй, фантазуй і твор
Скільки ще теорем невідкритих І задач нерозв'язаних є!
Хай живе математика в світі
Пісня про математику
(виконує група учнів)
Любі числа, теореми,
Формули чудовi,
Ви професiй нескiнченних Друзi i основа.
Приспiв.
Найдавнiша на планетi
Між наук цариця, — Математика — ти наша Вiрна помiчниця.
Використані джерела:
1. Технологія уроку математики 5-11 класи (Козира В.М., Тернопіль, «Астон», 2002 рік)
2. Відкриті уроки з математики (Харків, «Основа», 2006 рік)
3. Інтерактивні технології на уроках математики
(Харків, «Основа», 2007 рік)
4. Математичні чудеса і таємниці ( М.Гарднер, Москва,
«Наука», 1986 рік)
5. Алгебра і елементарні функції (Яремчук Ф.П.,
П.А. Рудченко, Київ, «Наукова думка», 1987 рік)
 |
про публікацію авторської розробки
Додати розробку