Дослідницька робота на уроці алгебри: "Формула коренів квадратного рівняння"
- Мета запропонованої дослідницької роботи допомогти учням “відкрити” алгоритми розв'язку квадратних рівнянь.Вчити учнів бачити аналогію задач, аналогію теорій.
- Для перевірки отриманих знань учням пропонуються індивідуальні диференційовані самостійні роботи за власним варіантом. ( а- власних варіант, порядковий номер в журналі. )
- Для проведення дослідницьких робіт застосовується технологія групової роботи. Кожній групі пропонуються завдання залежно від рівня складності (середній, достатній, високий )
- Група (4-5учнів) виконує проблемне завдання, яке є елементом загальної проблеми. Після обговорення робляться висновки. Всі учні мають можливість взяти участь в дослідженні з урахуванням власних творчих здібностей.
Дослідницька робота з учнями на уроці алгебри в 8 класі.
Вчитель: Ласкіна С.М
Тема: Формула коренів квадратного рівняння. .
Мета: Вивести формулу для ров’язування квадратних рівнянь. Формувати уміння ров’язувати квадратні рівняння виділенням квадрата двочлена.
Всі рівняння розв’ язанні в групах , записуються на дошці.
Група 1. ( середній рівень).
Розв’язати рівняння х2 – 10х + 9 = 0 способом виділення квадрата двочлена. Скільки коренів має рівняння ?
х2 - 2 *5х + 25 – 25 + 9 = 0
( х – 5 )2 = 16
х – 5 = 4 х – 5 = -4
х = 9 х = -4 + 5
х = 1
Відповідь: 1; 9.
Група 2. (середній рівень).
Розв’язати рівняння х2 – 10х + 25 = 0. Скільки коренів має рівняння ?
( х – 5 )2 = 0
х = 5
Відповідь: 5.
Група 3. (середній рівень).
Розв’язати рівняння х2 – 10х + 100 = 0.
х2 - 2 *5х + 25 – 25 + 100 = 0
( х – 5 )2 = -75
розв’язків немає.
Група 4. (достатній рівень).
Розв’язати рівняння х2 – 10х + 15 = 0.
х2 - 2 *5х +52 – 5 2 + 15 = 0
( х – 5 )2 - 10 = 0
( х – 5 )2 = 10
х – 5 =![]() х – 5 = -
х – 5 = - ![]()
х = ![]() х = -
х = - ![]()
Відповідь: - ![]() ,
, ![]() .
.
Група 5. (достатній рівень).
Розв’язати рівняння 3х2 + 2х - 1 = 0
Домножимо на 3:
9х2 + 6х - 3 = 0
(3х)2 + 2 3х 1 + 1 – 1 – 3 = 0
( 3х + 1 )2 - 4 = 0
3х + 1 = 2 3х + 1 = -2
3х = 1 3х = -3
х = ![]() х = -1
х = -1
Відповідь: ![]() , -1.
, -1.
Група 6. (високий рівень).
Розв’язати рівняння х2 + 3х – 4 = 0
х2 + 2 ![]()
![]()
![]()
![]()
х + ![]() х +
х + ![]()
х = ![]() х = -
х = -![]()
Відповідь: -4; 1.
Група 7 ( сильні ). ах2 + вх + с = 0
Домножити на 4а
4ах2 + 4авх + 4ас = 0
(2ах)2 + 2 2ах в + в2 + 4ас = 0
( 2ах + в )2 = в2 – 4ас
2ах + в = ![]() або 2ах + в = -
або 2ах + в = - ![]()
х1 =![]() х2 =
х2 = ![]()
![]()
![]()
Обговорення.
- Скільки розв’язків може мати повне квадратне рівняння ?
( 1, 2, не має ров’язків ).
- Які числа можуть бути розв’язками квадратного рівняння ?
( R дійсні )
- Коли незручно застосовувати спосіб виділення квадрата двочлена ?
- Коли рівняння має один корінь ?
![]() = 0 , в2 – 4ас = 0.
= 0 , в2 – 4ас = 0.
- Коли рівняння не має коренів ?
в2 – 4ас ![]() .
.
6. Коли рівняння має 2 корені ?
в2 – 4ас ![]() .
.![]()
Висновок ( робить вчитель)
Вираз в2 – 4ас називають дискримінантом ( латинське diskriminans – розрізняючий ).
D = в2 – 4ас
ах2 + вх + с = 0
D = в2 – 4ас
Якщо D = 0, то х = -![]() ,
,
D![]() , то х1,2 =
, то х1,2 = ![]()
D![]() , то коренів не має.
, то коренів не має.
Користуючись формулою коренів квадратного рівняння можна розв’ язати будь-яке квадратне рівняння.
Самостійна робота.
( за власним варіантом).
Варіант а – порядковий номер в журналі.
Розв’зати рівняння Відповіді
-
(а + 1) х2 – х – а = 0 1; -
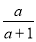
-
х2 + ах + 1000 = 0 коренів не має (якщо вар а
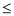 31)
31)
- ах2 + (а+1) х – (2а +1) + 0 один з коренів 1.
Додаткове завдання сильним учням.
- Довести, що в першому рівнянні при будь-якому значенні а один з коренів рівняння 1.
- Знайти номер варіанта при якому друге рівняння буде мати розв’язок.
1

про публікацію авторської розробки
Додати розробку
