Досвід роботи «Способи реалізації навчальної функції іспиту ЗНО з математики»

Харківська загальноосвітня школа І-ІІІ ступенів № 71
Харківської міської ради Харківської області

 

 

 

 

 

 

 

Досвід роботи вчителя

на тему

«Способи реалізації навчальної функції іспиту ЗНО з математики»

 

 

 

 

 

 

Виконала: вчитель вищої категорії, старший вчитель, вчитель математики Тетяна ЗРАЖЕВСЬКА

 

 

 

 

 

 

 

 

Харків – 2023

АНОТАЦІЯ

 

Узагальнення досвіду роботи на тему: «Способи реалізації навчальної функції іспиту ЗНО з математики» розроблено вчителем математики Харківської загальноосвітньої школи І-ІІІ ступенів № 71 Зражевською Тетяною Іванівною.

 

Метою роботи є розробка методів підготовки здобувачів освіти до ЗНО з математики, при яких значна увага приділяється організації діяльності вчителя щодо дидактично виваженого використання тестових технологій, що включає добір та/або самостійне створення тестових завдань різних форм та формування у здобувачів освіти навичок роботи з тестовим завданнями у форматі ЗНО, зокрема, ознайомлення їх із відповідними процедурами й алгоритмами виконання завдань різних форм та правилами оформлення робіт, виявлення типових й індивідуальних помилок та проведення відповідної роботи для усунення цих помилок.

ЗМІСТ
 

 

ЗМІСТ.................................................3

ВСТУП................................................4

РОЗДІЛ 1 ТЕОРЕТИЧНА ЧАСТИНА...........................6

1.1 Проблеми при підготовці до ЗНО

1.2 Методична підготовка

РОЗДІЛ 2 ПРАКТИЧНА ЧАСТИНА...........................11

2.1 Методичні рекомендації для підготовки учнів до виконання

завдань бланку А

2.2 Методичні рекомендації для підготовки учнів до виконання

завдань бланку Б

ВИСНОВКИ............................................16

СПИСОК ВИКОРИСТАННИХ ДЖЕРЕЛ........................17

ВСТУП

Впровадження зовнішнього незалежного оцінювання принесло гарні результати щодо значного підвищення якості середньої та вищої освіти в Україні, позитивно позначилося на загальному рівні освіченості та стало вагомим фактором у боротьбі з корупцією.

З уведенням  зовнішнього незалежного оцінювання   українська освіта потребує переосмислення підходів до освітнього процесу, оскільки сучасний студент повинен бути конкурентоспроможним, здатним застосовувати набуті знання й навички в реальному житті.

Запорукою успішного проходження ЗНО є завчасна підготовка до нього. У сучасній практиці тестові технології контролю навчальних досягнень посідають належне місце, бо забезпечують найбільш об’єктивне і всебічне оцінювання досягнень учнів із навчального предмета.

Мета: розробка методів підготовки здобувачів освіти до ЗНО з математики, при яких значна увага приділяється організації діяльності вчителя щодо дидактично виваженого використання тестових технологій, що включає добір та/або самостійне створення тестових завдань різних форм та формування у здобувачів освіти навичок роботи з тестовим завданнями у форматі ЗНО, зокрема, ознайомлення їх із відповідними процедурами й алгоритмами виконання завдань різних форм та правилами оформлення робіт, виявлення типових й індивідуальних помилок та проведення відповідної роботи для усунення цих помилок.

Об'єктом дослідження: підготовка учнів до зовнішнього незалежного оцінювання з математики.

Предмет дослідження: методки підготовки здобувачів освіти до ЗНО з математики

Актуальність розробки методик підготовки учнів до ЗНО пов'язана з тим, що після введення в шкільну практику Зовнішнього незалежного оцінювання виникло безліч проблем, як у вчителів, так і в учнів. ЗНО в Україні почало формуватись з 2004 року, і з того часу вийшло немало різної допоміжної літератури про те, що необхідно робити вчителям щоб покращити підготовку учнів для успішної здачі тестування.

Чи можуть школярі успішно здати Зовнішнє оцінювання без відповідної, спеціальної підготовки? Як показує практика – здобувачі освіти в результаті зіштовхуються з численними труднощами, як з психологічної, так і з методичної точки зору. Для вирішення психологічних труднощів потрібна система занять спрямована на зняття емоційної напруженості при здачі іспиту в новій, не звичній для школярів формі. Частина проблем безпосередньо пов'язана з традиційною подачею матеріалу в шкільних підручниках. Учні не готові і не завжди вміють виконувати завдання в тестовій формі. Для вирішення цієї проблеми необхідно вирішувати завдання не тільки в вигляді тестів, а й приділяти велику увагу розв’язуванню задач різними способами. Розібрати, які помилки допускаються учнями при вирішенні тих чи інших типів завдань найчастіше. В першу чергу потрібно проаналізувати методики підготовки учнів до успішної здачі випускного іспиту з математики в рамках ЗНО.

 

ОСНОВНІ МЕТОДИКИ ПО ПІДГОТОВЦІ ДО ЗНО З МАТЕМАТИКИ

 

1.1 Проблеми при підготовці до ЗНО

 

Результати ЗНО виявили ряд невирішених проблем, характерних для підготовки різних категорій випускників. Це дозволяє висловити деякі загальні рекомендації, спрямовані на вдосконалення процесу викладання і підготовки учнів середньої школи.

1. Необхідно вдосконалювати методику формування базових умінь, що становлять основу математичної підготовки випускників середньої школи.
2. Аналіз результатів виконання базових завдань з курсу алгебри та початків аналізу показав наявність позитивної динаміки в оволодінні матеріалом розділу «Тригонометрія». В той же ж час викликають тривогу невисокі результати виконання завдань по розв’язуванню ірраціональних рівнянь та логарифмічних нерівностей. Слід звернути більшу увагу для засвоєння учнями стандартних алгоритмів розв'язання завдань такого типу.
3. Геометрична підготовка випускників школи продовжує залишатися невисокою, тому як і раніше необхідно посилити увагу вчителів до викладання курсу геометрії в основній і старшій школі, щоб в процесі навчання учні не тільки опановували теоретичними фактами курсу, а й набували вміння проводити обґрунтовані міркування при вирішенні геометричних задач і математично грамотно записувати отримане рішення.
4. Найнижчі результати учні показали при вирішенні завдань, які найважче піддаються алгоритмізації: завдання з геометрії, завдання прикладного змісту (де потрібно застосувати вміння читати графіки, вирішувати сюжетні завдання), а також завдання, для розв’язування яких потрібно застосувати елементарні навички дослідницької роботи.
5. Також слабкою залишається підготовка учнів з питань: виконання спільних дій над звичайними і десятковими дробами; перетворення многочленів; перетворення алгебраїчних дробів; перетворення виразів, що містять степінь з цілим показником; перетворення ірраціональних виразів; розв’язування квадратних, дробово-раціональних рівнянь і нерівностей; визначення властивостей функції за допомогою графіка;

Починаючи викладати математику з 5 класу, у вчителя з'являється можливість, починати готувати школярів до ЗНО задовго до його початку. А саме посилено працювати над повторенням матеріалу і систематизацією знань, використовувати в процесі навчання різні види діяльності і нові форми контролю. Все це готує здобувачів освіти до іспиту як психологічно, так і дозволяє підвищити якість математичної освіти.

Щоб добре підготувати учнів до ЗНО, вчителю потрібно самому багато і постійно навчатися, удосконалювати свою майстерність, і поряд з традиційними підходами використовувати інноваційні технології та ресурси мережі Інтернет.

Школа сьогодні стрімко змінюється, намагається іти в ногу з часом. Важливо не стільки дати дитині якомога більший багаж знань, скільки забезпечити її загальнокультурний, особистісний і пізнавальний розвиток.

Серед різноманітних напрямків нових педагогічних технологій для досягнення поставленої мети вчителеві рекомендується використовувати в своїх методиках такі засоби:

• Навчання в співробітництві
• Метод проектів
• Індивідуальні консультації
• Робота в малих групах і парах
• Використання ІКТ

 

 

 

1.2. Методична підготовка

 

Багато вчителів, репетитори та батьків, які допомагають своїм дітям підготуватися до ЗНО, намагаються перерішувати якомога більше варіантів попередніх років. Такий шлях неперспективний. По-перше, варіанти не повторюються. По-друге, у школяра не формується стійкий загальний спосіб діяльності із завданнями відповідних видів. По-третє, у школяра з'являється почуття розгубленості і повної безнадійності: завдань так багато і всі вони такі різні. Запам'ятати рішення всіх завдань неможливо. Тому набагато розумніше вчити школярів загальним універсальним прийомам та підходам для розв’язування завдань.

Таким чином, підготовка не зводиться до «натаскування» випускника на виконання певного типу завдань, що містяться в демонстраційній версії іспиту. Підготовка до ЗНО означає вивчення програмного матеріалу з включенням завдань у формах, що використовуються при підсумковій атестації. Крім того, на початку першого семестру необхідно виявити сильні і слабкі сторони в знаннях учнів, на підставі цього створити цільові групи і сформулювати основні принципи побудови методичної підготовки до іспиту.

СИСТЕМА РОБОТИ ВЧИТЕЛЯ З ПІДГОТОВКИ УЧНІВ ДО УСПІШНОЇ ЗДАЧІ ЗНО В СУЧАСНИХ УМОВАХ. (ПРАКТИЧНА ЧАСТИНА)

 

2.1 Методичні рекомендації для підготовки учнів до виконання завдань бланку А

 

З введенням нової процедури атестації та проведення конкурсного іспиту до вузу перед учителем старших класів стоїть важливе завдання підготовки учнів до здачі ЗНО. При цьому їх потрібно не «натаскувати», а як вже говорилося навчити мислити, працювати самостійно.

Розглянемо деякі вправи, які потрібно опрацювати з учнями для успішної здачі ЗНО, так як таким завданням і методам їх розв’язання не завжди представлена достатня увага в сучасних підручниках для старшої школи.

Завдання 1. Спростити вираз .

1) 1; 2) 19; 3) 1; 4) 19.

Розв’язок. Крім традиційного способу – застосування основних тригонометричних тотожностей, для розв’язування даного завдання можливий і інший підхід.

Зауважимо, що жодна з відповідей не залежить від х, тому в початковий вираз замість х підставимо будь-яке «зручне» число. Нехай, наприклад, х=0. Тоді, підставляючи в початковий вираз, отримаємо:

Завдання розв’язане: тільки одна відповідь збігається з 1, тому вона і є правильною. Вірна відповідь - перша.

Завдання 2. Спростити вираз

1) ; 2) ; 3) ; 4) .

Перший спосіб. Нехай а=32 (2⁵), тоді значення виразу дорівнює . Тільки при підстановці в перший варіант відповіді а=32 ми отримаємо відповідь .

Другий спосіб. Позначивши . Тоді . Теперь 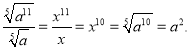Отже, вірна відповідь - перша

Завдання 3. Обчислити якщо

1) ;  2) -1;  3) 4;  4) .

Перший спосіб. Із умови знаходимо, що . Тоді

Другий спосіб Вірна відповідь - друга.

Завдання 4. Знайдіть всі корені рівняння

1) 2) 3) 4)

Перший розв’язок. Зауважимо, що та можна виразити через Отже, рівняння зводиться до найпростішого відносно. А якщо це так, то найбільш вірогідною є третя відповідь.

Другий розв’язок. Оскільки у всіх відповідях , то припустимо, що n=0. відповіді приймуть вигляд: 0; 0. Перша і четверта відпадають, оскільки при цих значеннях рівняння не визначено, а друга відповідь легко усувається перевіркою (ліва частина є ірраціональним числом, а права – раціональним). Вірна відповідь - третя.

Завдання 5. Вкажіть первісну функції .

1) ; 2) 3) 4)

Розв’язок. Це завдання простіше вирішувати диференціюючи функції, дані у відповідях. При диференціюванні не відбувається подвоєння аргументу, тому 1 і 3 відповіді відпадають. Четверта відповідь відпадає, оскільки похідна не збігається з. Залишається єдина відповідь - друга.

Розглянувши ці завдання можна зробити наступні висновки:

Дані розв’язки доступні для більшості учнів, тому стає очевидною необхідність і доцільність продумувати систему вправ, націлену на підготовку до успішного виконання подібних завдань всіма школярами. Відзначимо також, що ця робота не повинна здійснюватися тільки в 10-11 класах, як це робиться тепер через те, що змінилася система атестації. Необхідно починати з 7 класу. Скажімо, добре знання і застосування властивостей лінійної функції повинна забезпечувати програма 7 класу, а властивості квадратичної функції – програма 8 класу і т. д.

Наведемо приклади деяких вправ з різними способами розв’язування, які можна використовувати при роботі з учнями для підготовки до ЗНО.

Вирази і перетворення. У зв'язку з тим, що вирази і перетворення використовуються при вирішенні багатьох типів завдань, зупинимося тільки на декількох.

Завдання. Спростити вираз .

1) ; 2) 3; 3) 0; 4) .

Перший розв’язок. Послідовно перетворюємо:

.

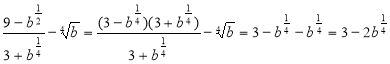Правильною є перша відповідь.

Другий розв’язок.  Нехай Тоді і вираз набуде вигляду

Третій розв’язок. Позначимо вихідний вираз через F (b).

1. Обчислимо значення виразу при b=1:

 

2. Відразу видно, що відповіді 2 і 3 не можуть бути вірними.

3. Тепер обчислимо значення першої та четвертої відповідей при b=1:

та

Звідси випливає, що правильною є перша відповідь.

Коментар.

Перше розв’язком зазвичай користуються школярі, які твердо засвоїли програму і вміють контролювати свої дії. Він аналогічний рішенню, яке виконують учні при написанні письмової контрольної роботи після вивчення теми. Якщо завдання буде дещо ускладнено (збільшено число елементів і їх різноманітність), то час виконання може серйозно зрости. Для реалізації такого розв’язку потрібно тверде знання формул скороченого множення і хороші навички виконання перетворень.

Другий розв’язок можна рекомендувати тим школярам, які допускають обчислювальні помилки і не завжди бачать «потрібні» формули. При збільшенні складності час виконання зросте незначно. Реалізація такого розв’язку передбачає вміння побачити потрібну заміну і використати відповідну формулу.    

Третій розв’язок істотно відрізняється від перших двох. Він реалізується з урахуванням наступного міркування: якщо при якомусь допустимому значенні змінної значення вихідного виразу і відповіді відрізняються, то ця відповідь не є правильним. Звідси випливає, що якщо при якомусь значенні змінної всі значення відповідей, крім однієї, відрізняються від значення вихідного виразу, то правильним і буде та відповідь, значення якої дорівнює значенню вихідного виразу.

2.2 Методичні рекомендації для підготовки учнів до виконання завдань бланку Б

 

Друга частина істотно відрізняється від першої. Основна відмінність полягає в наступному.

1. Пропонується завдання без варіантів відповіді. У кожному завданні слід її знайти і записати.

2. Завдання даної частини більш складні. Складність завдань пов'язана з тим, що розв’язок кожної задачі це, як правило, рішення двох - трьох стандартних завдань, об'єднаних одним формулюванням. Наприклад, пропонується не просто вирішити тригонометричне рівняння, а потрібно знайти кількість коренів на заданому відрізку (або їх суму).

З. Не всі завдання цієї частини рівноцінні. Але при їх виконанні не потрібно оформляти розв’язок і обґрунтовувати хід розв’язок, досить дати вірну відповідь.

4. При виконанні завдань другої частини можна використовувати будь-які факти, навіть маловідомі в шкільній практиці, сміливо користуватися ними для економії часу, не ризикуючи при цьому абсолютно нічим.

Наведемо факти, що дозволяють економити час виконання завдань другої частини.

1. Підібрати корінь многочлена F(х) і розділити многочлен на різницю отримавши його розкладання.

2. Знати і вміти застосовувати формулу складних відсотків.

3. Вміти вирішувати досить складну за формулюванням задачу графічно. При цьому допускаються готові шаблони. Наприклад, побудова графіка функції починати з побудови вертикальної і горизонтальної асимптот ( і відповідно).

4. Використовувати будь-які відомі формули, а не тільки ті, які представлені в підручнику.

 

ВИСНОВКИ

 

Практика показує, що навіть у здобувачів 10-11 класів здатність до усвідомленої самоосвіти традиційно є недостатньо високою і потребує стимулювання. Саме тому, й підготовка до ЗНО випускників ЗЗСО, повинна здійснюватися під керівництвом педагога-наставника на всіх етапах освітнього процесу (як під час вивчення нового матеріалу, так і під час його закріплення та перевірки, зокрема, й за допомогою тестових завдань для поточного та тематичного контролю). При цьому особлива увага має приділятися організації діяльності вчителя щодо дидактично виваженого використання тестових технологій, що включає добір та/або самостійне створення тестових завдань різних форм та формування у здобувачів освіти навичок роботи з тестовим завданнями у форматі ЗНО, зокрема, ознайомлення їх із відповідними процедурами й алгоритмами виконання завдань різних форм та правилами оформлення робіт, виявлення типових й індивідуальних помилок та проведення відповідної роботи для усунення цих помилок.

Аналіз підручників дає можливість зробити висновок, що тестові завдання в них не охоплені всіма формами, які використовуються під час зовнішнього незалежного оцінювання, та представлені здебільшого завданнями закритої форми з вибором однієї або кількох правильних відповідей. Це, на нашу думку, недостатньо розвиває відповідні вміння та навички здобувачів освіти щодо роботи з тестовими завданнями різних форм. При цьому підручники характеризуються потужним дидактичним потенціалом у забезпеченні формування предметних та ключових компетентностей здобувачів освіти, що представлено розміщенням в них достатньої кількості проблемних, дослідницьких і творчих завдань. Отже, підручник для закладів середньої освіти може бути інструментом підготовки здобувачів освіти до зовнішнього незалежного оцінювання. Проте треба враховувати обмежені можливості підручника у формуванні навичок виконання тестових завдань різних форм. Адже, сучасний підручник виконує багато дидактичних функцій, а через обмежені обсяги він не може містити велику кількість різнопланових завдань і вправ. У сучасних умовах підручник повинен розглядатися лише як складова навчально-методичного комплекту, який міститиме також спеціально розроблені навчальні посібники для підготовки до ЗНО, електронні освітні ресурси, що будуть забезпечувати дистанційне тестування, тощо.

Робота по підготовці до ЗНО буде ефективною, якщо в систему роботи школи і кожного класу окремо буде включено проведення, як мінімум, один раз на місяць тренінгів з подальшим якісним аналізом виконуваних робіт. Однак аналіз робіт учнів не повинен зводитися до виставлення балів і показу правильного розв’язку – він повинен включати всі можливі способи рішень кожного завдання і порівняння цих способів з урахуванням їх ефективності, естетики і тимчасових витрат. Особливо слід при цьому продумувати ті варіанти рішень, які не були реалізовані школярем, і розповісти їм про втрачені можливості.

Але підготовка учнів до ЗНО не повинна бути самоціллю вчителя при роботі з одинадцятикласниками і, тим більше, не повинна зводитися тільки до неї. Вчити міркувати і доводити, правильно застосовувати необхідні і достатні умови, вчити індукції і дедукції, аналізу і синтезу, узагальненню і конкретизації, вмінню будувати приклади і приводити контрприклади, розвивати грамотну математичну мову, вивчати яскраві факти з історії математики і життя математиків, навчати дослідницькому підходу, самостійної дослідницької діяльності – як були, так і залишаються основними завданнями вивчення математики в старшій школі.

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Айзенберг М.І. Навчання учнів методам самостійної роботи з підручником // Математика в школі. №6. – 1982.
2. Арутюнян Є.Б., Глазков Ю. А., Левітас Г. Г. Взаємне навчання школярів на уроках математики // Математика в школі. №4. – 1988.
3. Гібш і.А. Розвиток мовлення в процесі вивчення шкільного курсу математики // Математика в школі. №6. – 1995.
4. .Захарійченко Ю.О., О. В. Школьний. Повний курс математики в тестах. Харків, «Ранок».-2020
5. Л.О. Денищева, Ю. А. Глазков, К. А. Краснянська. Математика: збірник завдань. М.: Просвіта-2005.
6. Л.О. Денищева, Ю. А. Глазков, К. А. Краснянська та ін. Методика підготовки: книга для вчителя. М.: Просвіта-2005.
7. Капіносов А., Білоусова Г., Гап'юк Г., Мартинюк С., Олійник Л., Ульшин П., Чиж О. Математика. Комплексне видання. Харків, «Ранок».-2021
8. Колягін Ю.М., Ткачова М.И., Федорова Н. є. профільна диференціація навчання математики // Математика в школі. №4. – 1990.
9. Манвелов С. Г. Завдання на розвиток самоконтролю учнів. М.: Просвітництво. – 1997.
10. Нелін Є. П. Математика. Експрес-підготовка. Харків, «Ранок».-2021
11. Рижик В. І. 30000 уроків математики. М.: Просвітництво. – 2010.