Довідковий матеріал до теми "Геометричні переміщення"

ГЕОМЕТРІЯ, 9    ТЕМА 5. ГЕОМЕТРИЧНІ ПЕРЕМІЩЕННЯ

Переміщення – це перетворення фігури, при якому зберігаються відстані між її точками.

                        Під час переміщення: образом прямої є пряма; образом променю є промінь;
                        образом кута є рівний йому кут; образом відрізка є рівний йому відрізок.

Образом  точки  A(x; y)  фігури  F  при  переміщенні
на координатній площині є точка A′(x; y ) фігури F′

Означення        Дві фігури називають рівними, якщо існує переміщення, при якому одна

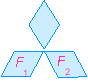                             з даних фігур є образом другої. Запис F = F₁ означає, що фігури F і F₁ рівні.

                   Властивості рівних фігур

1. Якщо F = F₁, то F₁ = F;
2. Якщо F = F₁ та F₁ = F₂, то F = F₂;
3. Якщо F = F₁, то існує деяке переміщення, що переводить фігуру F у фігуру F₁.

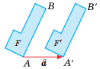Означення. Паралельним перенесенням на вектор називається перетворення,
при якому кожна точка A фігури F переходить у точку A′ фігури F′ так, що AA′ = .

Властивості. Паралельне перенесення є переміщенням.

Якщо фігура F′ - образ фігури F при паралельному перенесенні, то F’ = F.

          Образом прямої є сама пряма або паралельна їй пряма.

Паралельне перенесення на вектор задається формулами:
x = x + a, y = y + b,  де = .

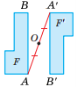Означення. Точки А і А’ називаються симетричними відносно точки О, якщо точка О – середина відрізка АА’. О – центр симетрії; АО = ОА’.

Означення. Симетрією відносно точки О називають перетворення фігури F у фігуру F’,
при якому кожна точка A фігури F симетрична відносно точки О точці A′ фігури F’.

                               Властивості. Симетрія відносно точки О є переміщенням.

Якщо фігури F і F′, симетричні відносно точки О, то F = F’.

               Образом прямої є сама пряма або паралельна їй пряма.

Симетрія відносно початку координат задається формулами:

x = -x, y = -y, де точка О (0; 0) – середина відрізка АА’.

Центрально-симетричні фігури: пряма; відрізок; паралелограм; правильний многокутник; коло і круг.

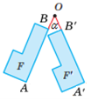  Означення. Поворотом навколо точки О на кут  називається перетворення фігури F
   у фігуру F’, при якому ОА′ = ОА та АОА′ = .

                     О – центр повороту,  - кут повороту; ОА = ОА’ , АОА’ = .

Властивості. Поворот навколо точки О на кут  є переміщенням.

                           Якщо фігура F′ - образ фігури F при повороті, то F’ = F.

Поворот точки одиничного кола навколо початку координат О (0; 0) на кут 90 проти годинникової стрілки задається формулами: x = -y, y = x, ОА = ОА’ = 1, АОА’ = 90.

Поворот точки одиничного кола навколо початку координат О (0; 0) на кут 90 за годинниковою стрілкою задається формулами: x = y, y = -x, де ОА = ОА’ = 1, АОА’ = 90.

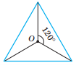
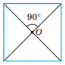
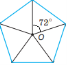
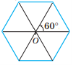
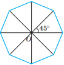
Поворотну симетрію має: коло; круг; правильний многокутник (кут повороту кратний ).

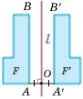Означення. Точки А і А’ називаються симетричними відносно прямої l, якщо пряма l
є серединним перпендикуляром відрізка АА’.

Означення. Симетрією відносно  прямої l називають перетворення фігури F у фігуру F, при якому кожна точка А фігури F симетрична відносно прямої l точці А’ фігури F ‘.

                   l – вісь симетрії; АА₁  l, АО = OА’. Кожна точка осі симетрична сама собі.

Властивості. Симетрія відносно прямої l є переміщенням.

             Якщо фігури F і F′, симетричні відносно прямої l , то F = F’.

Фігури, які симетричні відносно прямої: пряма; відрізок; кут; рівнобедрений і правильний трикутники; ромб; прямокутник; квадрат; рівнобедрена трапеція.

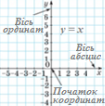
Симетрія відносно осі ординат задається формулами: x = -x, y = y.

Симетрія відносно  осі  абсцис задається формулами:  x = x, y = -y.

Симетрія відносно прямої у = х задається формулами: x = y, y = x.