Урок на тему "Квадратний тричлен".

Урок № 46                                                                          Дата    08.04.2020р.

 

Доброго ранку або дня, шановні мої учні!

Я рада знову вас привітати на нашому виртуальному уроці.

 Гадаю, за час карантину, ви вже склали собі розпорядок дня та працюєте за ним.

Час минає і сьогодні я запропоную вам долучитися до нового виду роботи – тести онлайн. Для того, щоб пройти його з кращим результатом, уважно читайте питання, думайте і не поспішайте.

Пам´ятайте: “Кто спешит, тот людей смешит”.

Пройшовши тест, незабудьте відправити мені свій результат  (на диск або на ел. пошту)

                             

Сподіваюсь на плідну роботу та взаємоповагу!

А тепер до роботи!

Відкрийте зошит і записуйте:

Восьме  квітня

Класна робота

Тема уроку     Квадратний тричлен.

Мета уроку: вивчити означення квадратного тричлена і кореня квадратного тричлена. Спонукати учнів до прояву творчої активності, ініціативи. Розвивати логічне мислення, інтелектуальні здібності, формувати пізнавальний інтерес до математики.

Тип уроку:

Хід уроку

 

І. Актуалізація опорних знань

Любі друзі, для того, щоб вміло розкладати квадратний тричлен, треба добре розв´язувати  квадратні рівняння. Наступний тест покаже на скільки добре ви це вмієте робити. Повідомляю вам:

Завдання необхідно виконати до  10 квітня 17:00 

 

Код доступу 133545

Прошу вас  використати цей код,
відкривши посилання      join.naurok.ua

 

Всі питання і відповіді обовязково записати у робочий зошит!

Бажаю вам успіхів!

ІІ. Сприймання та усвідомлення нового матеріалу.

     Стародавній грецький вчений Аристотель вважав, що запитання є переходом від незнання до знань. Дійсно це так. Адже вони допоможуть нам розглянути  вивчені теми з усіх сторін, виділити головне, а також пов’язати його з раніше вивченим матеріалом.

 

Квадратний тричлен.

Квадратним тричленом називають многочлен виду ах² + bх + с, де х змінна, а,b і с деякі числа, причому a 0.

Наведемо приклади многочленів, які є квадратними тричленами:

2х² 5х + 3;      х² + 9х;      х²   7;     5х².

Зазначимо, що ліва частина квадратного рівняння ах² + bх + с = 0 є квадратним тричленом.

Коренем квадратного тричлена називають значення змінної, при якому значення квадратного тричлена дорівнює нулю.

Наприклад, число 4 є коренем квадратного тричлена х² х12.

Зрозуміло, щоб знайти корені квадратного тричлена ах² + bх + с, треба розв’язати відповідне квадратне рівняння ах² + bх + с = 0.

Дискримінантом квадратного тричлена ах² + bх + с є число b²4ас.

Якщо D 0, то квадратний тричлен коренів не має. Якщо D0, то квадратний тричлен має один корінь, якщо D 0,то два корені.

Розглянемо квадратний тричлен у ² + 3 у 4. Розкладемо його на множники методом групування.

Маємо: у ² + 3 у 4 = у ² + 4у у 4= у(у + 4) (у + 4) = (у + 4) (у

Даний квадратний тричлен  розкладено на лінійні множники

у + 4 і у

• Якщо дискримінант квадратного тричлена  ах² + bх + с додатний, то даний тричлен можна розкласти на лінійні множники:

                                            ах² + bх + с = а ( ) ( ),

           де і корені квадратного тричлена.

Зауваження. 

• Якщо дискримінант квадратного тричлена дорівнює нулю, то вважають, що квадратний тричлен має два рівні корені, тобто = 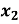. У цьому випадку розклад квадратного тричлена на множники має такий вигляд:

                                       ах² + bх + с = а (х )² .

• Якщо дискримінант квадратного тричлена від’ємний, то даний тричлен не можна розкласти на лінійні множники.

 

Стародавній грецький вчений Аристотель вважав, що запитання є переходом від незнання до знань. Дійсно це так. Адже вони допоможуть нам розглянути  вивчені теми з усіх сторін, виділити головне, а також пов’язати його з раніше вивченим матеріалом.

Для того, щоб ви відчули впевненість в своїх силах, ми застосуємо вивчений матеріал для розв’язування задач і вправ.

 

ІІІ. Застосування  вивченного матеріалу до розв’язування вправ.

№ 1.    Розкласти на лінійні множники квадратний тричлен:

а) х² + 8х + 15.

Прирівняємо квадратний тричлен до нуля:

х² + 8х + 15= 0.

Скористаємося теоремою Вієта: = 5; = .

Відповідь. х² + 8х + 15 = (х + 3) (х +5); 

 

 б) 6х² 5х 1.

Щоб знайти корені квадратного тричлена  ах² + bх + с, треба розв’язати відповідне квадратне рівняння ах² + bх + с =0.

Таким чином, 6х² 5х 1=0;  D = 25 4 6( = 25+24=49;

Відповідь. 6х² 5х 1=6(х + ) (х 1) = (6х + 1) (х

 

№ 2.    Скоротити дріб:

Розв’язання.

Прирівняємо чисельник до нуля: = 0;

Скористаємося теоремою Вієта: = 3;   = 2.

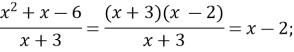
Відповідь. .

 

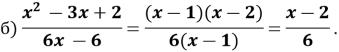
Прирівняємо чисельник до нуля: = 0. За теоремою Вієта:

 

№ 3.   Скоротити дріб:

Розв’язання.

Розкладемо чисельник на множники: 4а² = (2а3) (2а + 3).

Прирівняємо  до нуля,   = 0;

D = 8142(18) = 81 + 144 = 225;

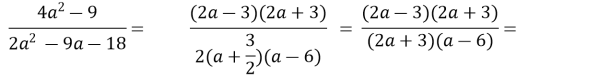
Відповідь..

 

Щоб кожний міг з впевненістю сказати, що він досяг успіху потрібно самостійно попрацювати над виконанням аналогічних завдань. Адже уміння працювати самостійно є дуже важливим етапом в навчанні та житті.

 

IV.  Підсумок уроку.

Прошу вас усно відповісти на питання:

1. Що називають дискримінантом квадратного тричлена?

2. У якому випадку квадратний тричлен не має коренів? має один корінь? має два корені?

3. У якому випадку квадратний тричлен можна розкласти на лінійні множники?

4. За якою формулою квадратний тричлен можна розкласти на лінійні множники?

5. У якому випадку квадратний тричлен не можна розкласти на лінійні множники?

Ось і закінчився наш урок. Дякую за співпрацю і чекаю на домашню роботу!!!

Відступіть, будь ласка, від класної роботи 4 клітинки вниз і записуємо:                   Восьме квітня

                                              Домашня  робота

 

V. Домашнє завдання:

 

№ 1.   Розкласти на лінійні множники квадратний тричлен: а) 

                                                                                                       б)  4х² + 3х 22; 

№ 2.   Скоротити дріб:   

 

 

Не забувайте  домашню роботу відправити на Google – диск.