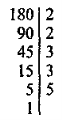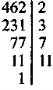Довідник для 6 класу з математики
Розкладання натуральних чисел на прості множники
|
|
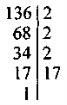
136 = 2 · 2 · 2 · 17 |
6 = 2 · 3;
10 = 2 · 5;
30 = 2 · 3 · 5;
48 = 2 · 2 · 2 · 2 · 3;
52 = 2 · 2 · 13;
72 = 2 · 2 · 2 · 3 · 3.
Алгоритм знаходження НСД
Цікаво, що розробив це загальне правило для знаходження НСД двох чисел відомий давньогрецький учений Евклід ще більше 2000 років тому.
- Розкласти числа на прості множники.
- Виписати спільні множники цих чисел.
- Знайти добуток спільних простих множників. Це і буде НСД даних чисел.
За цим правилом можна знайти також НСД для трьох і більше чисел.
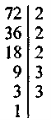
Наприклад: знайдіть НСД чисел 72, 84 і 180 (один учень працює біля дошки).
|
|
|
|
НСД(72; 84; 180) = 2 · 2 · 3 = 12.
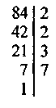
Завдання. Знайдіть НСД чисел 10 і 21 (один учень працює біля дошки).
|
|
|
НСД(10; 21) = 1.
Числа 10 і 21 називають взаємно простими.
Алгоритм знаходження НСК
- Розкласти дані числа на прості множники.
- Доповнити розклад одного з них тими множниками розкладу іншого числа, яких немає в розкладі першого.
- Обчислити добуток знайдених множників.
Наприклад. Знайти НСК(462; 420) (один учень працює біля дошки).
|
|
|
НСК(462; 420) = 2 · 3 · 7 · 11 · 2 · 5 = 4620.
Додавання і віднімання дробів з різними знаменниками
![]() .
.
![]() .
.
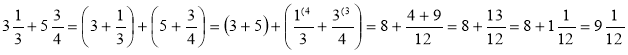 .
.
4) 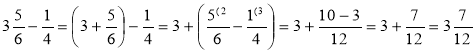 .
.
5)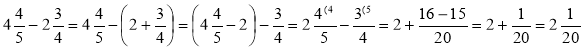 .
.
6) ![]() .
.
7) ![]() .
.
8) ![]() .
.
![]() .
.
![]() .
.
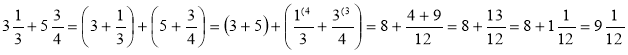 .
.
4) 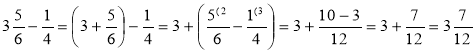 .
.
5)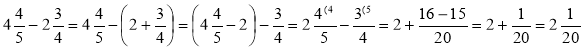 .
.
6) ![]() .
.
7) ![]() .
.
8) ![]() .
.
Додавання чисел з однаковими знаками – Додаємо, знак більшого.
(+3) + (+5) = +8
(-3) + (-5) = -8.
Додавання двох чисел з різними знаками. – Віднімаємо, знак більшого.
-5 + 7 = 2.
5 + (-7) = -2.
0 + (-7) = -7.
Віднімання чисел з однаковими знаками – Розкриваємо дужки:
(+3) - (+5) =3-5=-2
(-3) - (-5) = 3+5=8.
Віднімання двох чисел з різними знаками. – Розкриваємо дужки:
-5 - 7 = -12.
5 - (-7) = 5+7=12.
0 - (-7) = + 7.
Множення раціональних чисел. Множення двох чисел з різними знаками – знак мінус.
а · 1 = 1 · а = а;
(-a) · b = a · (-b) = -ab;
(a) · (-b) = ab;
а · (-1) = (-1) · а = -а;
а · 0 = 0.
Множення чисел з однаковими знаками – знак плюс.


про публікацію авторської розробки
Додати розробку