Довідник Вектори.Означення. Властивості. Приклади

Миколаївський національний університет
імені В.О. Сухомлинського
Кафедра математики та фізики
Вектори
Означення. Властивості. Приклади
Миколаїв
2019
Автор
Рєзнікова Л.В. студентка 112 групи
У даному посібнику в доступній, стислій та наочній формі (означення і приклад) вміщено матеріали за темою «Вектори».
Посібник призначений для учнів та вчителів загальноосвітніх шкіл, абітурієнтів, студентів, а також для всіх, хто цікавиться математикою.
Вектори.Означення.Властивості.Приклади.Посібник.- Миколаїв, 2019. – 24 с.
![]()
54030, м. Миколаїв, вул. Нікольська, 24,
МНУ імені В.О. Сухомлинського
Зміст
Формули визначення координат вектора заданого координатами його початкової і кінцевої точки
Приклади задач пов'язаних з визначенням координат вектора по двом точкам
Приклади задач на обрахунок довжини векторів
Властивість напрямних косинусів.
Формули обрахунку напрямних косинусів вектора
Приклади задач з напрямними косинусами вектора
Приклади задач на рівність векторів
Умови ортогональності векторів.
Приклади задач на ортогональність векторів
Колінеарність векторів, умови колінеарності векторів
Приклади задач на колінеарність векторів
Компланарність векторів. Умови компланарності векторів
Приклади задач на компланарність векторів
Формула обрахунку кута між векторами
Приклади задач на обрахунок кута між векторами
Проекція вектора на вісь. Проекція вектора на вектор
Обчислення проекції вектора на вектор
Приклади задач на проекцію вектора
Додавання і віднімання векторів
Формули додавання і віднімання векторів
Приклади задач на додавання і віднімання векторів
Формули множення вектора на число
Властивості добутку вектора на число
Приклади задач на множення вектора і числа
Формули скалярного добутку векторів заданих координатами
Властивості скалярного добутку векторів
Приклади задач на скалярний добуток векторів
 Означення. Вектор- це напрямлений відрізок, тобто відрізок, який має довжину і певний напрямок. Графічно вектори зображуються у вигляді напрямлених відрізків прямої певної довжини (рис.1).
Означення. Вектор- це напрямлений відрізок, тобто відрізок, який має довжину і певний напрямок. Графічно вектори зображуються у вигляді напрямлених відрізків прямої певної довжини (рис.1).
Позначення вектора
Вектор початком якого є точка А, а кінцем - точка В, позначається ![]() (рис.1). Також вектори позначають однією маленькою літерою, наприклад
(рис.1). Також вектори позначають однією маленькою літерою, наприклад ![]() .
.
Довжина вектора
Означення.Довжина напрямленого відрізка визначає числове значення вектора і називається довжиною вектора або модулем вектора AB.
Для позначення довжини вектора використовують дві вертикальні лінії зліва і справа |AB|.
Нульовийвектор
Означення. Нульовим вектором називається вектор, у якого початкова і кінцева точки співпадають.
Нульовий вектор зазвичай позначають як 0.
Довжина нульового вектора дорівнює нулю.
 Колінеарні вектори
Колінеарні вектори
Означення. Вектори, паралельні одній прямій або які лежать на одній прямій називають колінеарними векторами (рис. 2).
 Співнаправленівектори
Співнаправленівектори
Означення. Два колінеарних вектора ![]() . і
. і ![]() . називаються співнаправленими векторами, якщо їх напрямки співпадають: a↑↑b (рис. 3)
. називаються співнаправленими векторами, якщо їх напрямки співпадають: a↑↑b (рис. 3)
Протилежно направлені вектори
 Означення. Два колінеарних вектора a і b називаються протилежно направленими векторами, якщо їх напрямок протилежний: a↑↓b (рис. 4)
Означення. Два колінеарних вектора a і b називаються протилежно направленими векторами, якщо їх напрямок протилежний: a↑↓b (рис. 4)
Компланарні вектори
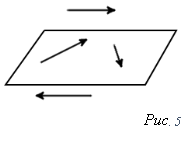 Означення. Вектори, паралельні одній площині або які лежать на одній площині називають компланарними векторами. (рис. 5). Завжди можливо знайти площину паралельну двом довільним векторам, тому будь-які два вектора завжди компланарні.
Означення. Вектори, паралельні одній площині або які лежать на одній площині називають компланарними векторами. (рис. 5). Завжди можливо знайти площину паралельну двом довільним векторам, тому будь-які два вектора завжди компланарні.
Рівні вектора
 Означення. Вектори a і b називаються рівними, якщо вони лежать на одній прямій або паралельних прямих, їх напрямки співпадають, а довжини рівні (рис. 6).
Означення. Вектори a і b називаються рівними, якщо вони лежать на одній прямій або паралельних прямих, їх напрямки співпадають, а довжини рівні (рис. 6).
Тобто, два вектори рівні, якщо вони колінеарні, співнаправлені та мають рівні довжини:
a = b, якщо a↑↑b і |a| = |b|.
Одиничний вектор
Означення. Одиничним векторомабо ортом - називається вектор, довжина якого дорівнює одиниці.
Основне співвідношення. Щоб знайти координати вектора AB, за координатами його початкової точки А і кінцевої точки В, необхідно від координат кінцевої точки відняти відповідні координати початкової точки.
Формули визначення координат вектора заданого координатами його початкової і кінцевої точки
Визначення координат вектора для плоских задач
![]()
У випадку плоскої задачі вектор AB заданий координатами точок A (Ax;Ay) і B (Bx;By) можна знайти скориставшись наступною формулою
Визначення координат вектора для просторових задач
![]()
У випадку просторової задачі вектор AB заданий координатами точок A (Ax; Ay; Az) і B (Bx; By; Bz) можна знайти скориставшись наступною формулою
Визначення координат вектора для n -вимірного простору
![]()
У випадку n-вимірного простору вектор AB заданий координатами точок A (A1; A2; ...; An) і B (B1; B2; ...; Bn) можна знайти скориставшись наступною формулою
Приклади задач пов'язаних з визначенням координат вектора по двом точкам
Приклади плоских задач
Приклад 1. Знайти координати вектора AB, якщо A(1; 4), B(3; 1).
Розв'язок: AB= {3 - 1; 1 - 4} = {2; -3}.
Приклад 2. Знайти координати точки B вектора AB= {5; 1}, якщо координати точки A (3; -4).
Розв'язок: ABx= Bx- Ax =>Bx= ABx + Ax => Bx = 5 + 3 = 8
ABy= By- Ay =>By= ABy + Ay => By = 1 + (-4) = -3
Відповідь: B(8; -3).
Приклади просторових задач
Приклад 3. Знайти координати вектора AB, якщо A (1; 4; 5), B (3; 1; 1).
Розв'язок: AB = {3 - 1; 1 - 4; 1 - 5} = {2; -3; -4}.
Приклад 4. Знайти координати точки A вектора AB = {5; 1; 4}, якщо координати точки B (3; -4; 1).
Розв'язок: ABx= Bx - Ax => Ax = Bx - ABx => Ax = 3 - 5 = -2
ABy= By - Ay => Ay = By - ABy => Ay = -4 - 1 = -5
ABz= Bz - Az => Az = Bz - ABz => Az = 1 - 4 = -3
Відповідь: A (-2; -5; -3).
Приклади для n -вимірного простору
Приклад 5. Знайти координати вектора AB, якщо A (1;4;5; 5; -3), B (3; 0; 1; - 2;5).
Розв'язок: АB = {3 - 1; 0 - 4; 1 - 5; -2 - 5; 5 - (-3)} = {2; -4; -4; -7; 8}.
Приклад 6. Знайти координати точки B вектора AB = {5; 1; 2; 1}, якщо координати точки A(3; -4; 3; 2).
Розв'язок: AB1 = B1 - A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8
AB2 = B2 - A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 - A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 - A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Відповідь: B(8; -3; 5; 3).
Означення. Довжина напрямленого відрізку визначає числове значення вектора і називається довжиною вектора або модулем вектора AB.
Для позначення довжини вектора використовують дві вертикальні лінії зліва та справа |AB|.
Основне співвідношення.
Довжина вектора |a| в прямокутних декартових координатах дорівнює квадратному кореню з суми квадратів його координат.
Формули довжини вектора
Довжина вектора для плоских задач
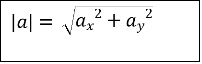
У випадку плоскої задачі модуль вектора ![]() = {ax; ay} можна знайти скориставшись наступною формулою:
= {ax; ay} можна знайти скориставшись наступною формулою:
Довжина вектора для просторових задач
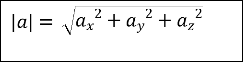
У випадку просторової задачі модуль вектора ![]() = {ax; ay; az} можна знайти скориставшись наступною формулою:
= {ax; ay; az} можна знайти скориставшись наступною формулою:
Довжини n -вимірного вектора
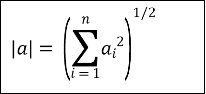
У випадку n-вимірного простору модуль вектора ![]() = {a1; a2; ... ; an} можна знайти скориставшись наступною формулою:
= {a1; a2; ... ; an} можна знайти скориставшись наступною формулою:
Приклади задач на обрахунок довжини векторів
Приклади обрахунку довжини вектора для плоских задач
Приклад 1. Знайти довжину вектора ![]() = {2; 4}.
= {2; 4}.
Розв'язок: ![]() .
.
Приклади обрахунку довжини вектора для просторових задач
Приклад 2. Знайти довжину вектора ![]() = {2; 4; 4}.
= {2; 4; 4}.
Розв'язок: ![]() .
.
Приклади обрахунку довжини вектора для просторів
з розмірністю більшою за 3
Приклад 3. Знайти довжину вектора ![]() = {1; -3; 3; -1}.
= {1; -3; 3; -1}.
Розв'язок:![]() .
.
Означення. Напрямні косинуси вектора (направляючі косинуси вектора) ![]() – це косинуси кутів, які вектор утворює з додатними півосями координат. Напрямні косинуси однозначно задають напрямок вектора.
– це косинуси кутів, які вектор утворює з додатними півосями координат. Напрямні косинуси однозначно задають напрямок вектора.
Основне співвідношення.
Щоб знайти напрямні косинуси вектора ![]() необхідно відповідні координати вектора поділити на модуль вектора. Відповідні координати одиничного вектора дорівнюють його напрямними косинусам.
необхідно відповідні координати вектора поділити на модуль вектора. Відповідні координати одиничного вектора дорівнюють його напрямними косинусам.
Властивість напрямних косинусів.
Сума квадратів напрямних косинусів дорівнює одиниці.
Формули обрахунку напрямних косинусів вектора
 Обрахунок напрямних косинусів вектора для плоских задач
Обрахунок напрямних косинусів вектора для плоских задач
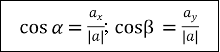
У випадку плоскої задачі (рис. 7) напрямні косинуси вектора ![]() = {ax;ay} можна знайти скориставшись наступною формулою:
= {ax;ay} можна знайти скориставшись наступною формулою:
Властивість: cos2 α + cos2 β = 1
Обрахунок напрямних косинусів вектора для просторових задач

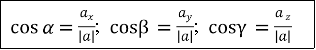
У випадку просторової задачі (рис. 8) напрямні косинуси вектора ![]() = {ax; ay; az} можна знайти скориставшись наступною формулою:
= {ax; ay; az} можна знайти скориставшись наступною формулою:
Властивість: cos2 α + cos2 β + cos2 γ = 1
Приклади задач з напрямними косинусами вектора
Приклади плоских задач з напрямними косинусами вектора
Приклад 1. Знайти напрямні косинуси вектора ![]() = {3; 4}.
= {3; 4}.
Розв'язок:
Знайдемо модуль вектора ![]() :
: ![]()
Знайдемо напрямні косинуси вектора ![]() :
:
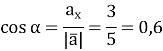
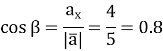
Відповідь: напрямні косинуси вектора cos α = 0.6, cos β = 0.8.
Приклад 2. Знайти значення вектора ![]() , якщо його довжина дорівнює 26, а напрямні косинуси cos α = 5/13, cos β = -12/13.
, якщо його довжина дорівнює 26, а напрямні косинуси cos α = 5/13, cos β = -12/13.
Розв'язок:
ax = ![]() ·cos α = 26 · 5/13 = 10
·cos α = 26 · 5/13 = 10
ay = ![]() cos β = 26 · (-12/13) = -24
cos β = 26 · (-12/13) = -24
Відповідь: ![]() = {10; -24}.
= {10; -24}.
Приклади просторових задач з напрямними косинусами вектора
Приклад 3. Знайти напрямні косинуси вектора![]() = {2; 4; 4}.
= {2; 4; 4}.
Розв'язок:
Знайдемо модуль вектора ![]() :
:
![]()
![]()
![]()
![]() ;
; ![]()
Відповідь: напрямні косинуси вектора cos α = 13, cos β = 23, cos γ = 23
 Означення. Вектори
Означення. Вектори ![]() і
і ![]() називаються рівними, якщо вони мають однакову довжину, лежать на паралельних прямих або на одній прямій, і напрямлені в один бік. (рис. 9). Тобто якщо, два вектора рівні, якщо вони колінеарні, співнаправлені і мають рівні довжини:
називаються рівними, якщо вони мають однакову довжину, лежать на паралельних прямих або на одній прямій, і напрямлені в один бік. (рис. 9). Тобто якщо, два вектора рівні, якщо вони колінеарні, співнаправлені і мають рівні довжини:
![]() , якщо
, якщо ![]() і
і ![]()
Умова рівності векторів.
Приклади задач на рівність векторів
Приклади плоских задач на рівність векторів
Приклад 1. Визначити які з векторів рівні ![]() = {1; 2},
= {1; 2}, ![]() = {1; 2},
= {1; 2}, ![]() ={3; 2}.
={3; 2}.
Розв'язок: ![]()
![]()
![]()
Приклад 2. При якому значенні параметра n вектори ![]() {1; 8;} і
{1; 8;} і ![]() = {1; 2n} рівні.
= {1; 2n} рівні.
Розв'язок: Перевіримо рівність компонент векторів
ax = bx = 1
ay = by => 8 = 2n => n = 8/2 = 4
Відповідь: при n = 4 вектори![]() і
і ![]() рівні.
рівні.
Приклади просторових задач на рівність векторів
Приклад 3. Визначити які з векторів рівні ![]() = {1; 2; 4},
= {1; 2; 4}, ![]() = {1; 2; 2},
= {1; 2; 2}, ![]() = {1; 2; 4}.
= {1; 2; 4}.
Розв'язок: ![]()
![]()
![]()
Приклад 4. При якому значенні параметра n вектори ![]() = {1; 2; 4} і
= {1; 2; 4} і ![]() = {1; 2; 2n} рівні.
= {1; 2; 2n} рівні.
Розв'язок: Перевіримо рівність компонент векторів
ax = bx = 1
ay = by = 2
az = bz => 4 = 2n => n = 4/2 = 2
Відповідь: при n = 2 вектори ![]() і
і ![]() рівні.
рівні.
Вектори рівні, якщо їх координати рівні.
Означення. Вектори ![]() і
і ![]() називаються ортогональними, якщо кут між ними дорівнює 90°. (рис. 10).
називаються ортогональними, якщо кут між ними дорівнює 90°. (рис. 10).
Умови ортогональності векторів.
Два вектори ![]() і
і ![]() ортогональні (перпендикулярні), якщо їх скалярний добуток дорівнює нулю.
ортогональні (перпендикулярні), якщо їх скалярний добуток дорівнює нулю.
![]()
Приклади задач на ортогональність векторів
Приклади плоских задач на ортогональність векторів
Так у випадку плоскої задачі для векторів ![]() = {ax; ay} і
= {ax; ay} і ![]() = {bx; by} умова ортогональності запишеться наступним чином:
= {bx; by} умова ортогональності запишеться наступним чином:
![]() = ax · bx + ay · by = 0
= ax · bx + ay · by = 0
Приклад 1. Довести що вектори ![]() = {1; 2} і
= {1; 2} і ![]() = {2; -1} ортогональні.
= {2; -1} ортогональні.
Розв’язок: Знайдемо скалярний добуток цих векторів:
![]() = 1 · 2 + 2 · (-1) = 2 - 2 = 0
= 1 · 2 + 2 · (-1) = 2 - 2 = 0
Відповідь: так як скалярний добуток дорівнює нулю, то вектори ![]() і
і ![]() ортогональні.
ортогональні.
Приклад 2. Перевірити чи є вектори ![]() = {3; -1} і
= {3; -1} і ![]() = {7; 5} ортогональними.
= {7; 5} ортогональними.
Розв’язок: Знайдемо скалярний добуток цих векторів:
![]() = 3 · 7 + (-1) · 5 = 21 - 5 = 16
= 3 · 7 + (-1) · 5 = 21 - 5 = 16
Відповідь: так як скалярний добуток не дорівнює нулю, то вектори ![]() і
і ![]() не ортогональні.
не ортогональні.
Приклад 3. Знайти значення числа n при якому вектори ![]() = {2; 4} і
= {2; 4} і ![]() = {n; 1} будуть ортогональні.
= {n; 1} будуть ортогональні.
Розв’язок: Знайдемо скалярний добуток цих векторів:
![]() = 2 · n + 4 · 1 = 2n + 4
= 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2
Відповідь: вектори ![]() і
і ![]() будуть ортогональні, якщо n = -2.
будуть ортогональні, якщо n = -2.
Приклади просторових задач на ортогональність векторів
Так у випадку просторової задачі для векторів ![]() = {ax; ay; az} і
= {ax; ay; az} і ![]() = {bx; by; bz} умова ортогональності запишеться наступним чином:
= {bx; by; bz} умова ортогональності запишеться наступним чином:
![]() = ax · bx + ay · by + az · bz = 0
= ax · bx + ay · by + az · bz = 0
Приклад 4. Довести що вектори ![]() = {1; 2; 0} і
= {1; 2; 0} і ![]() = {2; -1; 10} ортогональні.
= {2; -1; 10} ортогональні.
Розв'язок: Знайдемо скалярний добуток цих векторів:
![]() = 1 · 2 + 2 · (-1) + 0 · 10 = 2 - 2 + 0 = 0
= 1 · 2 + 2 · (-1) + 0 · 10 = 2 - 2 + 0 = 0
Відповідь: так як скалярний добуток дорівнює нулю, то вектори ![]() і
і ![]() ортогональні.
ортогональні.
Приклад 5. Перевірити чи є вектори ![]() = {2;3;1} і
= {2;3;1} і ![]() = {3;1;-9} ортогональними.
= {3;1;-9} ортогональними.
Розв'язок: Знайдемо скалярний добуток цих векторів:
![]() = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
= 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
Відповідь: так як скалярний добуток дорівнює нулю, то вектори ![]() і
і ![]() ортогональні.
ортогональні.
Приклад 6. Знайти значення числа n при якому вектори ![]() = {2; 4; 1} і
= {2; 4; 1} і![]() = {n; 1; - 8} будуть ортогональні.
= {n; 1; - 8} будуть ортогональні.
Розв'язок: Знайдемо скалярний добуток цих векторів:
![]() = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 - 8 = 2n - 4
= 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 - 8 = 2n - 4
2n - 4 = 0
2n = 4
n = 2
Відповідь: вектори ![]() і
і ![]() будуть ортогональні, якщо n = 2.
будуть ортогональні, якщо n = 2.
Колінеарність векторів, умови колінеарності векторів
 Означення. Вектори, що паралельні одній прямій або лежать на одній прямій називаються колінеарними векторами (рис. 11).
Означення. Вектори, що паралельні одній прямій або лежать на одній прямій називаються колінеарними векторами (рис. 11).
Умови колінеарності векторів
Два вектора будуть колінеарні при виконанні будь якої з цих умов:
Умова колінеарності векторів 1.
Два вектора ![]() і
і ![]() колінеарні, якщо існує число n таке, що
колінеарні, якщо існує число n таке, що ![]()
Умова колінеарності векторів 2.
Два вектора колінеарні, якщо відношення їх координат рівні.
ЗАУВАЖЕННЯ. Умову 2 неможливо застосувати, якщо один з компонентів вектора дорівнює нулю.
Умова колінеарності векторів 3.
Два вектори колінеарні, якщо їх векторний добуток дорівнює нуль вектору.
 ЗАУВАЖЕННЯ. Умова 3 може бути застосована лише для тривимірних (просторових) задач.
ЗАУВАЖЕННЯ. Умова 3 може бути застосована лише для тривимірних (просторових) задач.
Приклади задач на колінеарність векторів
Приклади задач на колінеарність векторів на площині
Приклад 1. Які з векторів ![]() = {1; 2},
= {1; 2}, ![]() = {4; 8},
= {4; 8}, ![]() = {5; 9} колінеарні?
= {5; 9} колінеарні?
Розв'язок: Так як вектори не містять компоненти що дорівнюють нулю, то скористаємось другою умовою колінеарності, яка у випадку плоскої задачі для векторів ![]() і
і ![]() буде мати наступний вигляд:
буде мати наступний вигляд:
![]() .
.
Тобто:
![]()
![]()
![]()
Приклад 2. Довести що вектори ![]() = {0; 3} і
= {0; 3} і ![]() = {0; 6} колінеарні.
= {0; 6} колінеарні.
Розв'язок: Так як вектори мають компоненти що дорівнюють нулю, то скористаємось першою умовою колінеарності, знайдемо чи існує таке число n для якого: ![]()
Для цього знайдемо ненульовий компонент вектора ![]() в даному випадку це ay. Якщо вектори колінеарні тоді
в даному випадку це ay. Якщо вектори колінеарні тоді ![]()
Знайдемо значення n ![]() : n
: n![]() = {2 · 0; 2 · 3} = {0; 6}
= {2 · 0; 2 · 3} = {0; 6}
Так як ![]() , то вектори
, то вектори ![]() колінеарні.
колінеарні.
Приклад 3. Знайти значення параметра n при якому вектори ![]() = {3; 2} і
= {3; 2} і ![]() = {9; n} колінеарні.
= {9; n} колінеарні.
Розв'язок: Так як вектори не містять компонентів рівних нулю, то скористаємось другою умовою колінеарності ![]() . Тобто:
. Тобто: ![]() . Розв'яжемо це рівняння:
. Розв'яжемо це рівняння: ![]()
Відповідь: вектори ![]() і
і ![]() колінеарні коли n = 6.
колінеарні коли n = 6.
Приклади задач на колінеарність векторів в просторі
Приклад 4. Які з векторів ![]() = {1; 2; 3},
= {1; 2; 3}, ![]() = {4; 8; 12},
= {4; 8; 12}, ![]() = {5; 10; 12} колінеарні?
= {5; 10; 12} колінеарні?
Розв'язок: Так як вектори не містять компоненти що дорівнюють нулю, то скористаємось другою умовою колінеарності, яка у випадку просторової задачі для векторів ![]() і
і ![]() буде мати наступний вигляд:
буде мати наступний вигляд:![]() .
.
Тобто: ![]()
![]()
![]()
Приклад 5. Довести що вектори ![]() = {0; 3; 1} и
= {0; 3; 1} и ![]() = {0; 6; 2} колінеарні.
= {0; 6; 2} колінеарні.
Розв'язок: Так як вектори мають компоненти що дорівнюють нулю, то скористаємось першою умовою колінеарності, знайдемо чи існує таке число n для якого:![]() . Для цього знайдемо ненульовий компонент вектора
. Для цього знайдемо ненульовий компонент вектора ![]() в даному випадку це ay. Якщо вектори колінеарні тоді
в даному випадку це ay. Якщо вектори колінеарні тоді ![]() . Знайдемо значення n
. Знайдемо значення n![]() : n
: n![]() = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
= {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так як ![]() , то вектори
, то вектори ![]() і
і ![]() колінеарні.
колінеарні.
Приклад 6. Знайти значення параметрів n і m за яких вектори ![]() = {3; 2; m} і
= {3; 2; m} і ![]() = {9; n; 12} колінеарні.
= {9; n; 12} колінеарні.
Розв'язок: Так як вектори не містять компонентів рівних нулю, то скористаємось другою умовою колінеарності ![]() тобто:
тобто:![]() .
.
З цього співвідношення отримаємо два рівняння:![]() та
та ![]()
Розв'яжемо ці рівняння: ![]() та
та ![]()
Відповідь: вектори ![]() і
і ![]() колінеарні коли n = 6 і m = 4.
колінеарні коли n = 6 і m = 4.
 Компланарність векторів. Умови компланарності векторів
Компланарність векторів. Умови компланарності векторів
Означення. Вектори, які паралельні одній площині або лежать на одній площині називаються компланарними векторами (рис. 12). Завжди можливо знайти площину паралельну двом довільним векторам, тому будь-які два вектори завжди компланарні.
Умови компланарності векторів
Для 3-х векторів. Три векторі компланарні якщо їх мішаний добуток дорівнює нулю.
Для 3-х векторів. Три вектори компланарні якщо вони лінійно залежні.
Для n векторів. Вектори компланарні якщо серед них не більш ніж два лінійно незалежних векторів.
Приклади задач на компланарність векторів
Приклад 1. Перевірити чи(довести що) компланарні три вектора ![]() ={1;2;3},
={1;2;3}, ![]() ={1;1;1},
={1;1;1}, ![]() = {1; 2; 1}.
= {1; 2; 1}.
Розв'язок: Знайдемо мішаний добуток цих векторів
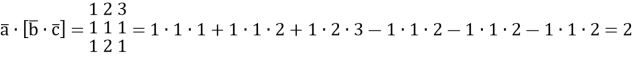
Відповідь: вектори не компланарні так, як їх мішаний добуток не дорівнює нулю.
Приклад 2. Перевірити чи компланарні вектори ![]() = {1; 1; 1},
= {1; 1; 1}, ![]() = {1; 2; 0},
= {1; 2; 0}, ![]() = {0; -1; 1},
= {0; -1; 1}, ![]() = {3; 3; 3}.
= {3; 3; 3}.
 Розв'язок: Знайдемо кількість лінійно незалежних векторів, для цього запишемо значення векторів в матрицю, і виконаємо над нею елементарні перетворення
Розв'язок: Знайдемо кількість лінійно незалежних векторів, для цього запишемо значення векторів в матрицю, і виконаємо над нею елементарні перетворення

Так як залишилось лише дві ненульові стрічки, то серед приведених векторів лише два лінійно незалежних вектора.
Відповідь: вектори компланарні так, як серед приведених векторів лише два лінійно незалежних вектора.
Означення. Кутом між двома векторами, відкладеними від однієї точки, називається найкоротший кут(рис.13), на який потрібно повернути один з векторів навколо свого початку до положення співнаправленості з іншим вектором.
Основне співвідношення. Косинус кута між векторами дорівнює скалярному добутку векторів, поділеному на добуток модулів векторів.
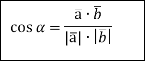
Формула обрахунку кута між векторами
Приклади задач на обрахунок кута між векторами
Приклади обрахунку кута між векторами для плоских задач
Приклад 1. Знайти кут між векторами ![]() = {3; 4} і
= {3; 4} і ![]() = {4; 3}.
= {4; 3}.
Розв'язок: Знайдемо скалярний добуток векторів:
![]() = 3 · 4 + 4 · 3 = 12 + 12 = 24.
= 3 · 4 + 4 · 3 = 12 + 12 = 24.
Знайдемо модулі векторів:
![]() ;
; ![]()
Знайдемо кут між векторами: ![]()
Приклади обрахунку кута між векторами для просторових задач
Приклад 2. Знайти кут між векторами ![]() = {3; 4; 0} і
= {3; 4; 0} і ![]() = {4; 4; 2}.
= {4; 4; 2}.
Розв'язок: Знайдемо скалярний добуток векторів:
![]() = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
= 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Знайдемо модулі векторів:
![]() ;
;
![]()
Знайдемо кут між векторами: ![]()
 Проекція вектора на вісь. Проекція вектора на вектор
Проекція вектора на вісь. Проекція вектора на вектор
Означення.Проекцією вектора ![]() на вісь l називається число, що дорівнює величині відрізку AlBl на вісі l, де точки Al і Bl є проекціями точок A і B на вісь l. (рис. 14).
на вісь l називається число, що дорівнює величині відрізку AlBl на вісі l, де точки Al і Bl є проекціями точок A і B на вісь l. (рис. 14).
Означення. Проекцією вектора ![]() на напрямок вектору
на напрямок вектору ![]() , називається число, яке дорівнює величині проекції вектора
, називається число, яке дорівнює величині проекції вектора ![]() на вісь, що проходить через вектор
на вісь, що проходить через вектор ![]() .
.
Обчислення проекції вектора на вектор
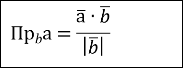
Для обрахунку проекції вектора ![]() на напрямок вектора
на напрямок вектора ![]() з означення скалярного добутку отримана формула:
з означення скалярного добутку отримана формула:
Приклади задач на проекцію вектора
Приклади обчислення проекції вектора для плоских задач
Приклад 1. Знайти проекцію вектора ![]() = {1; 2} на вектор
= {1; 2} на вектор ![]() = {3; 4}.
= {3; 4}.
Розв'язок: Знайдемо скалярний добуток цих векторів
![]() = 1·3 + 2·4 = 3+8 =11.
= 1·3 + 2·4 = 3+8 =11.
Знайдемо модуль вектора
![]() :
: ![]()
Знайдемо проекцію вектора ![]() на вектор
на вектор ![]()
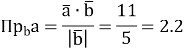
Відповідь:![]() = 2.2.
= 2.2.
Приклади обчислення проекції вектора для просторових задач
Приклад 2. Знайти проекцію вектора ![]() = {1; 4; 0} на вектор
= {1; 4; 0} на вектор ![]() = {4; 2; 4}.
= {4; 2; 4}.
Розв'язок: Знайдемо скалярний добуток цих векторів
![]() = 1·4 + 4·2 +0·4= 4+8+0 =12.
= 1·4 + 4·2 +0·4= 4+8+0 =12.
Знайдемо модуль вектора
![]()
Знайдемо проекцію вектора ![]() на вектор
на вектор ![]()

Відповідь: ![]() = 2.
= 2.
Додавання і віднімання векторів
Означення. Додавання векторів (сума векторів) ![]() +
+ ![]() - це операція знаходження вектора
- це операція знаходження вектора ![]() , всі елементи, якого дорівнюють попарній сумі відповідних елементів векторів
, всі елементи, якого дорівнюють попарній сумі відповідних елементів векторів ![]() і
і ![]() , тобто кожен елемент вектора
, тобто кожен елемент вектора![]() дорівнює:
дорівнює:
сi = ai + bi
Означення. Різниця векторів (віднімання векторів)![]() -
- ![]() - це операція знаходження вектора
- це операція знаходження вектора ![]() , всі елементи, якого дорівнюють попарній різниці відповідних елементів векторів
, всі елементи, якого дорівнюють попарній різниці відповідних елементів векторів ![]() и
и![]() , тобто кожен елемент вектора
, тобто кожен елемент вектора ![]() дорівнює:
дорівнює:
сi = ai - bi
Формули додавання і віднімання векторів
Додавання і віднімання векторів для плоских задач
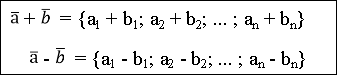
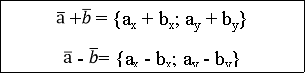
У випадку плоскої задачі суму та різницю векторів ![]() = {ax ; ay} і
= {ax ; ay} і
![]() = {bx ; by} можна знайти скориставшись наступними формулами:
= {bx ; by} можна знайти скориставшись наступними формулами:
Додавання і віднімання векторів для просторових задач
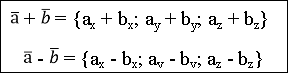
У випадку просторової задачі суму та різницю векторів ![]() = {ax ; ay ; az} і
= {ax ; ay ; az} і ![]() = {bx ; by ; bz} можна знайти скориставшись наступними формулами:
= {bx ; by ; bz} можна знайти скориставшись наступними формулами:
Додавання і віднімання n -вимірних векторів
У випадку n -вимірного простору суму та різницю векторів ![]() = {a1 ; a2 ; ... ; an} і
= {a1 ; a2 ; ... ; an} і ![]() = {b1 ; b2 ; ... ; bn} можна знайти скориставшись наступними формулами:
= {b1 ; b2 ; ... ; bn} можна знайти скориставшись наступними формулами:
Приклади задач на додавання і віднімання векторів
Приклади плоских задач на додавання і віднімання векторів
Приклад 1. Знайти суму векторів ![]() = {1; 2} і
= {1; 2} і ![]() = {4; 8}.
= {4; 8}.
Розв'язок: ![]() +
+ ![]() = {1 + 4; 2 + 8} = {5; 10}
= {1 + 4; 2 + 8} = {5; 10}
Приклад 2. Знайти різницю векторів ![]() = {1; 2} і
= {1; 2} і ![]() = {4; 8}.
= {4; 8}.
Розв'язок: ![]() -
-![]() = {1 - 4; 2 - 8} = {-3; -6}
= {1 - 4; 2 - 8} = {-3; -6}
Приклади просторових задач на додавання і віднімання векторів
Приклад 3. Знайти суму векторів ![]() = {1; 2; 5} і
= {1; 2; 5} і ![]() = {4; 8; 1}.
= {4; 8; 1}.
Розв'язок: ![]() +
+ ![]() = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6}
= {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6}
Приклад 4. Знайти різницю векторів ![]() = {1; 2; 5} і
= {1; 2; 5} і ![]() = {4; 8; 1}.
= {4; 8; 1}.
Розв'язок: ![]() -
-![]() = {1 - 4; 2 - 8; 5 - 1} = {-3; -6; 4}
= {1 - 4; 2 - 8; 5 - 1} = {-3; -6; 4}
Приклади задач на додавання і віднімання векторів з
розмірністю більше 3
Приклад 5. Знайти суму векторів ![]() = {1; 2; 5; 9} і
= {1; 2; 5; 9} і![]() = {4; 8; 1; -20}.
= {4; 8; 1; -20}.
Розв'язок: ![]() +
+ ![]() = {1 + 4; 2 + 8; 5 + 1; 9 + (-20)} = {5; 10; 6; -11}
= {1 + 4; 2 + 8; 5 + 1; 9 + (-20)} = {5; 10; 6; -11}
Приклад 6. Знайти різницю векторів ![]() = {1;2;5; -1;5} і
= {1;2;5; -1;5} і ![]() = {4;8;1;-1;2}.
= {4;8;1;-1;2}.
Розв'язок: ![]() -
-![]() = {1 - 4; 2 - 8; 5 - 1; -1 - (-1); 5- 2} = {-3; -6; 4; 0; 3}
= {1 - 4; 2 - 8; 5 - 1; -1 - (-1); 5- 2} = {-3; -6; 4; 0; 3}
Геометрична інтерпретація.
Добуток ненульового вектора на число - це вектор, колінеарний заданому (співнаправлений з заданим, якщо число додатне, протилежно направлений, якщо число від'ємне), а його модуль дорівнює модулю заданого вектора, помноженому на модуль числа.
Алгебраїчна інтерпретація.
Добуток ненульового вектора на число - це вектор, координати якого дорівнюють відповідним координатам даного вектора, помноженим на число.
Формули множення вектора на число
Множення вектора на число для плоских задач
![]()
У випадку плоскої задачі добуток вектора ![]() = {ax ; ay} та числа k можна знайти скориставшись наступною формулою:
= {ax ; ay} та числа k можна знайти скориставшись наступною формулою:
Множення вектора на число для просторових задач
![]()
У випадку просторової задачі добуток вектора ![]() = {ax ; ay ; az} і числа k можна знайти скориставшись наступною формулою:
= {ax ; ay ; az} і числа k можна знайти скориставшись наступною формулою:
Множення n -вимірного вектора
![]() У випадку n-вимірного простору добуток вектора
У випадку n-вимірного простору добуток вектора ![]() = {a1 ; a2; ... ; an} і числа k можна знайти скориставшись наступною формулою:
= {a1 ; a2; ... ; an} і числа k можна знайти скориставшись наступною формулою:
Властивості добутку вектора на число
Якщо вектор ![]() дорівнює добутку ненульового числа k і ненульового вектора
дорівнює добутку ненульового числа k і ненульового вектора ![]() , тобто
, тобто ![]() = k ·
= k · ![]() , тоді:
, тоді:
-
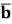 ||
|| 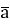 - вектори
- вектори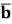 і
і 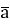 паралельні
паралельні
-
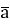 ↑↑
↑↑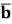 , якщо k > 0 - вектори
, якщо k > 0 - вектори 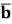 і
і 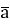 співнаправлені, якщо число k > 0
співнаправлені, якщо число k > 0
-
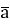 ↑↓
↑↓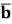 , якщо k < 0 - вектори
, якщо k < 0 - вектори 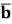 и
и 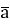 протилежно направлені, якщо число k < 0
протилежно направлені, якщо число k < 0
-
|
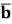 | = |k| · |
| = |k| · |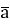 | - модуль вектора
| - модуль вектора 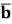 дорівнює модулю вектора
дорівнює модулю вектора 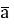 помноженому на модуль числа k
помноженому на модуль числа k
Приклади задач на множення вектора і числа
Приклад множення вектора на число для плоских задач
Приклад 1. Знайти добуток вектора ![]() = {1; 2} на 3.
= {1; 2} на 3.
Розв'язок:
3 · ![]() = {3 · 1; 3 · 2} = {3; 6}.
= {3 · 1; 3 · 2} = {3; 6}.
Приклад множення вектора на число для просторових задач
Приклад 2. Знайти добуток вектора ![]() = {1; 2; -5} на -2.
= {1; 2; -5} на -2.
Розв'язок:
(-2) · ![]() = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.
= {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.
Геометрична інтерпретація.
Скалярним добутком двох векторів ![]() і
і ![]() буде скалярна величина, яка дорівнює добутку модулів цих векторів помноженому на косинус кута між ними:
буде скалярна величина, яка дорівнює добутку модулів цих векторів помноженому на косинус кута між ними: ![]()
Алгебраїчна інтерпретація.
Скалярним добутком двох векторів ![]() і
і ![]() буде скалярна величина, яка дорівнює сумі попарного добутку відповідних координат векторів
буде скалярна величина, яка дорівнює сумі попарного добутку відповідних координат векторів ![]() і
і ![]()
Формули скалярного добутку векторів заданих координатами
Cкалярний добуток векторів заданих координатами
У випадку плоскої задачі скалярний добуток векторів ![]() = {ax ; ay} і
= {ax ; ay} і ![]() ={bx ; by} можна знайти скориставшись наступною формулою:
={bx ; by} можна знайти скориставшись наступною формулою:
![]()
Скалярний добуток векторів для просторових задач
У випадку просторової задачі скалярний добуток векторів ![]() = {ax ; ay ; az} і
= {ax ; ay ; az} і ![]() = {bx ; by ; bz} можна знайти скориставшись наступною формулою:
= {bx ; by ; bz} можна знайти скориставшись наступною формулою:
![]()
Cкалярний добутку n -вимірних векторів
![]() У випадку n-вимірного простору скалярний добуток векторів
У випадку n-вимірного простору скалярний добуток векторів ![]() = {a1 ; a2 ; ... ; an} і
= {a1 ; a2 ; ... ; an} і ![]() = {b1 ; b2 ; ... ; bn} можна знайти скориставшись наступною формулою:
= {b1 ; b2 ; ... ; bn} можна знайти скориставшись наступною формулою:
Властивості скалярного добутку векторів
-
Скалярний добуток вектора самого на себе завжди більше або дорівнює нулю:
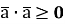
-
Скалярний добуток вектора самого на себе дорівнює нулю тоді і тільки тоді, коли вектор дорівнює нульовому вектору:

-
Скалярний добуток вектора самого на себе дорівнює квадрату його модуля:
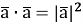 0
0
-
Операція скалярного добутку комутативна:
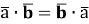
-
Якщо скалярний добуток двох не нульових векторів дорівнює нулю, то ці вектори ортогональні:

-
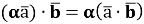
-
Операція скалярного добутку дистрибутивна:
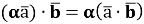
-
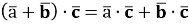
Приклади задач на скалярний добуток векторів
Приклади обрахунку скалярного добутку векторів для плоских задач
Приклад 1. Знайти скалярний добуток векторів ![]() = {1; 2} і
= {1; 2} і ![]() = {4; 8}.
= {4; 8}.
Розв'язок:
![]() = 1 · 4 + 2 · 8 = 4 + 16 = 20.
= 1 · 4 + 2 · 8 = 4 + 16 = 20.
Приклад 2. Знайти скалярний добуток векторів ![]() і
і ![]() , якщо їх довжини |
, якщо їх довжини |![]() | = 3, |
| = 3, |![]() | = 6, та кут між векторами дорівнює 60˚.
| = 6, та кут між векторами дорівнює 60˚.
Розв'язок:
![]() = |
= |![]() | · |
| · |![]() | cos α = 3 · 6 · cos 60˚ = 9.
| cos α = 3 · 6 · cos 60˚ = 9.
Приклад 3. Знайти скалярний добуток векторів ![]() =
= ![]() + 3
+ 3![]() і
і ![]() = 5
= 5 ![]() - 3
- 3![]() , якщо їх довжини |
, якщо їх довжини |![]() | = 3, |
| = 3, |![]() | = 2, та кут між векторами
| = 2, та кут між векторами ![]() і
і ![]() дорівнює 60˚.
дорівнює 60˚.
Розв'язок:
![]() ·
· ![]() = (
= (![]() + 3
+ 3![]() ) · (5
) · (5![]() - 3
- 3![]() ) = 5
) = 5 ![]() ·
·![]() - 3
- 3 ![]() ·
· ![]() + 15
+ 15 ![]() ·
· ![]() - 9
- 9 ![]() ·
·![]() =
=
= 5 |![]() |2 + 12
|2 + 12 ![]() ·
· ![]() - 9 |
- 9 |![]() |2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ - 9 · 22 = 45 +36 -36 = 45.
|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ - 9 · 22 = 45 +36 -36 = 45.
Приклад обрахунку скалярного добутку векторів для просторових задач
Приклад 4. Знайти скалярний добуток векторів ![]() = {1; 2; -5} і
= {1; 2; -5} і ![]() = {4; 8; 1}.
= {4; 8; 1}.
Розв'язок:
![]() = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 - 5 = 15.
= 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 - 5 = 15.
Приклад обрахунку скалярного добутку векторів для n -вимірних векторів
Приклад 5. Знайти скалярний добуток векторів ![]() ={1; 2; -5; 2} і
={1; 2; -5; 2} і
![]() ={4; 8; 1; -2}.
={4; 8; 1; -2}.
Розв'язок:
![]() = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 - 5 -4 = 11.
= 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 - 5 -4 = 11.


про публікацію авторської розробки
Додати розробку

