Методичні рекомендації«Застосування орігамі під час уроків геометрії»
Застосування орігамі при вивченні геометрії.
Тема: « Площина.Пряма.Промінь.»
Задача 1.Поділити відрізок на дві рівні частини,на чотири рівні частини,на вісім рівних частин.
Задача 2.На скільки частин ділять площину три прямі? Розглянути різні варіанти розташування прямих на площині.
Тема: «Площа. Формула площі прямокутника.»
Перший урок цієї теми можна присвятити квадрату. Розглянути його властивості, дати визначення певним елементам.

![]()
![]() А В
А В
![]()
![]()
D С
Точки А, В, С, D – вершини квадрата ,АВ, ВС, СD, DA – сторони квадрата, визначивши АВ = ВС = СD = DA, ВАD = CBA = DCB = ADC = 900
Задача 1:
- Як з листа прямокутної форми виготовити лист квадратної форми?
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Візьміть квадратний лист паперу та перегніть його поєднуючи вершини.
А та С

 А В
А В
АС – діиагональ квадрата АВСD
D С
- Знайдіть середини сторін AD та BC – точки M та N. Перегніть квадрат, з’єднуючи ці точки.
 А В
А В
![]()
М N MN – средня лінія квадрата АВСD
D С
- Скільки діагоналей та середніх ліній можна провести в квадраті? (дві)
- Що можна сказати про довжину середньої лінії квадрата? (рівна стороні квадрата)
- Якою властивістю володіє діагональ квадрата?Середня лінія? (поділяє квадрат на дві рівні фігури)
- Перегніть квадрат по діагоналям,спробуйте довести,що отримані при цьому трикутники рівні (співпадають при накладанні)
- Якими властивостями володіють ці трикутники? (прямокутні, равнобедрені)
Наприкінці уроку можна запропонувати учням скласти нескладну мордочку кота чи собаки.
Мордочка кішки
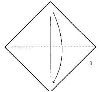
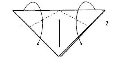
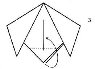
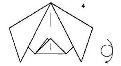
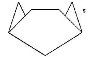
 6
6
- Складіть лист по діагоналі
- Зігніть куточки вниз
- Зігніть два нижніх кута вперед
- Переверніть
- Мордочка кішки готова
Мордочка собаки
1.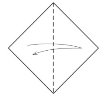 2.
2.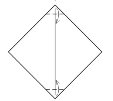 3.
3.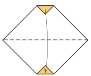 4.
4.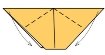 5.
5.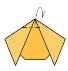 6.
6.
- Складіть лист по діагоналі
- Зігніть куточки вниз
- Зігніть верхній кут вперед
- Відігніть обидва кута назад
- Мордочка готова
В якості домашнього завдання можна запропонувати учням розфарбувати своїх тваринок та вигадати історію про зустріч кота чи собаки з Квадратиком.
При вивченні властивостей площ можна використовувати групову технологію, запропонувавши кожній групі розв’язати задачі та відповісти на питання:
- Зігніть квадрат по діагоналі.Чи будуть рівні площі отриманих трикутників?Чому? Чи будуть рівні їх периметри? Чому?
- Зігніть квадрат по середній лінії.Чи будуть рівні площі отриманих прямокутників?Чому?Чи будуть рівні їх периметри?Чому?
- Сформулюйте властивість площі рівних фігур.
- Знайдіть центр квадрата.Зєднайте вершини квадрата з його центром. Розгорніть квадрат.Що можна сказати про площі чотирикутника,що отримався внутрі квадрата та про площі трикутників по краям?
- Сформулюйте властивість площі фігури,що складається з кількох фігур.
Розглянувши разом з вчителем формули для площі прямокутника та квадрата, групи розв’язують наступні задачі:
Задача 2: Беремо прямокутний лит паперу та з’єднуємо його протилежні вершини.
Чи будуть рівні трикутники,що ми отримали?Чому?
Що можна сказати про площі цих трикутників?
Як можна обрахувати площу кожного?
Які вимірювання треба виконати. Щоб знайти площі трикутників та прямокутника?
Задача 3: Чотири сестри вирішили зайнятися квітами. Бабуся відгородила їм квадратну ділянку і запропонувала розділити на чотири частини рівної площі . щоб нікого не засмутити. Сіли сестри на порозі хатинки і почали розв’язувати бабусіну задачу. Кожна запропонувала свій варіант розділу ділянки. А скільки варіантів запропонуєте ви? (Можливо цю задачу запропонувати на домашнє завдання).
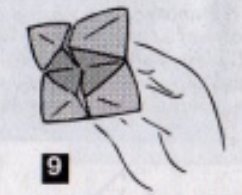
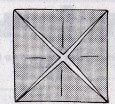
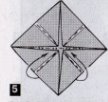
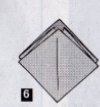
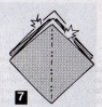
Наприкінці уроку можна запропонувати учням скласти пастку для мікробів у садку.
1.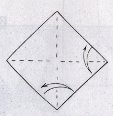 2.
2. 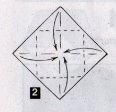 3.
3. 
 4.
4. 
5.  6.
6.  7.
7. 
 8.
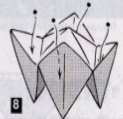
8. 
|
|
Опис роботи:
1.Беремо квадрат розміром 2020 см 2.згинаємо по діагоналях,згинаємо вершини квадрата до його центра. 3.Переверніть роботу. 4.Зігніть вершини квадрата до його центра. 5.Згибайте одночасно по всім указаним лініям. 6.Перевірте результат та поверніть фігуру навпаки. 7. Розкрийте чотири кармани. 8.Засуньте в них чотири пальці однієї руки. 9.Пастка готова. |
Тема: « Кут. Прямий та розгорнутий кут.
Вимірювання кутів. Транспортир»
За допомогою орігамі наочно ілюструється істинність двох теорем геометрії: про суму кутів трикутника та суму гострих кутів прямокутного трикутника.
Сума кутів трикутника дорівнює 1800.
Наочна ілюстрація істиності (у кожного учня модель трикутника):
Зєднайте точки M і N, де M і N відповідно середини сторін АВ і ВС
 1. В
1. В
![]()
![]()
![]()
![]() M N
M N
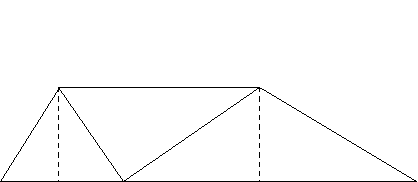 А С
А С
М N
![]() N
N
А Н(В) С
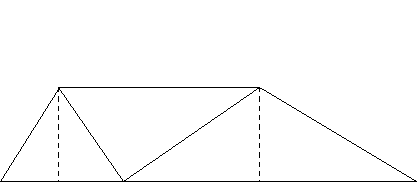
2. М M N
![]()
![]()
![]()
![]()
![]()
![]()
А H(В) С
Зігнути кути трикутника так, щоб точки А і Н, С і Н співпали


 3. М N
3. М N
Н(А,В,С)
Всі кути трикутника, зустрівшись в точці Н, складуть в сумі розгорнутий кут,що дорівнює 1800.
Сума гострих кутів прямокутного трикутника дорівнює 900.
Запропонуйте учням довести теорему за допомогою орігамі.

A Зігніть трикутник по середнім лініям
N MN и NK
М
В К С
![]() М N Гострі кути без накладань складають
М N Гострі кути без накладань складають
прямий кут 900.
В(А,С) К
Задачі на побудову :
- Поділити прямий кут навпіл.
- Поділити прямий кут на чотири рівні частини.
- *Поділити прямий кут на три рівні частини.
* - задача підвищеної складності
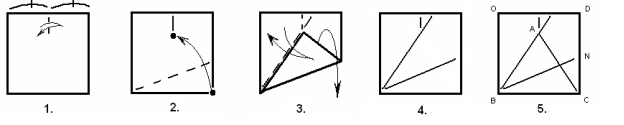 Розвязання до задачі №3
Розвязання до задачі №3
- Виконайте перегин,що ділить верхню сторону квадрата навпіл.
- Сумістіть вершину правого нижнього кута квадрата з деякою точкою на лінії перегину.
- Зігніть ліву верхню частину фігури і поверніться у початкове положення квадрата.
- Перевірте результат . Вершина лівого нижнього кута квадрата лініями згину разділена на три рівних кути.
Задачі на обчислення:
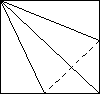
- Беремо квадратний аркуш паперу АВСD. Згинаємо по діагоналі. До діагоналі згинаємо дві суміжні сторони квадрата,що вийшли з вершини А.
 А В
А В
H
D M С
![]()
![]()
![]() Знайти градусні міри кутів АВН, АНC, АНМ
Знайти градусні міри кутів АВН, АНC, АНМ
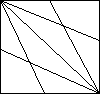
- Беремо квадратний аркуш паперу АВСD. Повторюємо дії попередньої задачі. Згинаємо до діагоналі дві суміжні сторони, що виходять з вершини D.
Р
![]() А В
А В
![]() К Н
К Н
D M C
![]() Знайти градусні міри кутів AFC, кути чотирикутника AFCE.
Знайти градусні міри кутів AFC, кути чотирикутника AFCE.
- Беремо квадратний аркуш паперу АВСD. Помічаємо перегин,що ділить верхню сторону квадрата навпіл. Суміщуємо вершину правого нижнього кута квадрата з деякою точкою на лінії перегину. Суміщуємо вершину лівого нижнього кута з тією ж точкою.
 1. 2.
1. 2.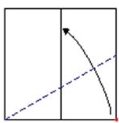 3.
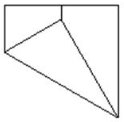
3. 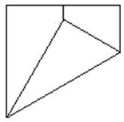 4.
4. 
![]()
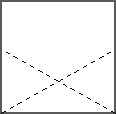 А В
А В
М Р
![]()
5. D C
Знайти градусну міру кутів ![]() MDC,
MDC, ![]() DKC,
DKC, ![]() DKM
DKM
Тема: «Коло та правильні многокутники»
Задача 1: За допомогою перегинів знайти центр вирізаного з паперу кола.
1.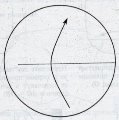 2.
2. 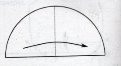 3.
3. 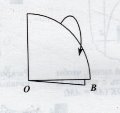 4.
4. 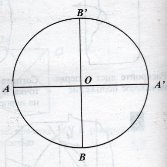
Задача 2: За допомогою перегинів поділіть круг на чотири рівні частини, на вісім рівних частин. (Точки на колі буду вершинами відповідно квадрата і правильного восьмикутника).
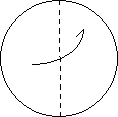
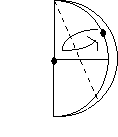
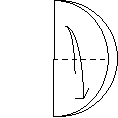
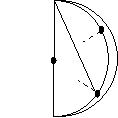
Задача 3: За допомогою перегинів поділіть круг на три рівні частини, шість рівних частин.
![]()
 А А А А
А А А А
![]()
![]()
![]()
![]()
![]() C С
C С
![]()
![]()
![]()
![]()
![]()
![]()
-
 2. 3. D 4. D
2. 3. D 4. D
В В В D В
 A Опис роботи:
A Опис роботи:
![]() E C 1. Зігніть круг навпіл
E C 1. Зігніть круг навпіл
2. Перегніть навпіл так, щоб точки А і В співпали
5. F D О- центр кола
B 3. Перегніть так, щоб лінія сгибу проходила через точку А, а точка О співпала з деякою точкою на дузі кола. Означимо цю точку С
- Лініями сгиба позначимо на дузі точки С и D. Розгорнемо. Засічки з лівого боку означимо відповідно точками Е та F
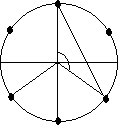
- Точки A,D и F поділяють коло на три рівні частини ( АОD = 1200)
- Точки А, С, D, В, F, E поділяють коло на шість рівних частин
Задача 4: За допомогою перегинів отримайте з квадрата правильний шестикутник, правильний трикутник. (Правильний шестикутник учні отримують разом з вчителем, повторюючи його дії).
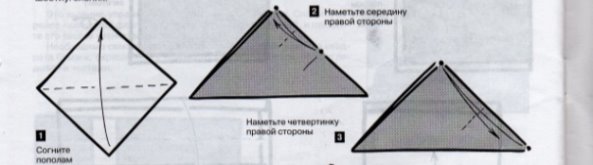
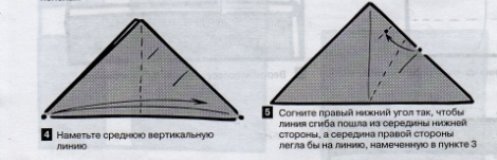
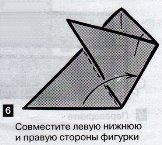
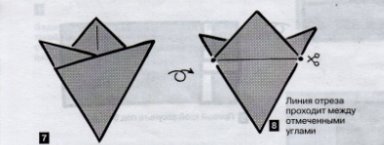
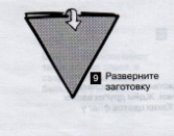

Задача 5: За допомогою перегинів правильного шестикутника з’ясуйте властивість його сторони , та обрахуйте величини кутів.
Задача 6: Як можна обрахувати площу правильного шестикутника? Виконайте необхідні вимірювання та знайдіть цю площу.
Тема: «Симетрія»
При вивченні центральної симетрії за допомогою орігамі можна розв’язати задачі:
Задача 1: За допомогою перегинів знайти центр симетрії квадрата.
Задача 2: За допомогою перегинів знайти центр симетрії прямокутника.
Задача 3: За допомогою перегинів знайти центр симетрії круга.
Задача 4: За допомогою перегинів знайти центр симетрії правильного шестикутника.
При знайомстві з осьовою симетрією є можливість виконати практичні завдання.
Задача1: Кожен учень бере аркуш паперу, виконуючи на ньому кольоровим олівцем або крейдою фігуру, потім проводе пряму і перегинає по ній аркуш так, щоб отримався відбиток фігури. В результаті отримаються фігури симетричні відносно прямої.
Питання: Чи можливо їх назвати симетричними?
Відповідь: Так,якщо перегнемо аркуш паперу по прямой, то фігури співпадуть, значить вони симетричні відносно цієї прямої.
Питання: Чи можна їх назвати рівними?
Відповідь : Так, вони. співпали при накладанні.
Задача 2: За готовими схемами запропонувати учням скласти модель метелика.
Довести,що метелик – симетрична фігура відносно прямої. (Учні перегинають виготовленого метелика і бачать,що лінія згину поділяє фігуру на дві частини, які співпадають. Лінія згину – вісь симетрії)

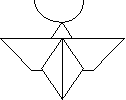 1.
1. 2.
2. 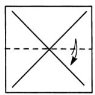 3.
3. 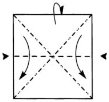 4.
4. 
![]()
![]()
![]()
![]()
![]()
![]() 5.
5.  6. 7. 8.
6. 7. 8.
Опис роботи:
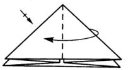
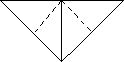
1. Перегніть квадрат по діагоналях. Переверніть.
2. Перегніть навпіл, суміщуючи верхню і нижню сторони.
3. Натисніть знизу на центр квадрата. Зігніть бічні трикутники,складаючи їх навпіл.При цьому верхня частина квадрата зігнеться на іншу сторону.
4. Перегортайте фігурку змінюючи місцями кутки.
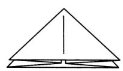
5. Базова форма «Подвійний трикутник»
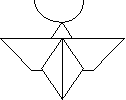
6. Поклавши заготовку середнім углом вниз, верхні кути відігніть вниз до середнього і поверніть фігуру оберненою стороною.
7. Нижний кут (середній) загніть вверх так, щоб він виступав від краю горизонтальної частини, розкрийте і розплющіть два маленьких кармана по бічним сторонам.
8. Приклейте вусики (робимо вдома)
![]()
 a Задача 3: Укажіть на плакаті (плакат з метеликом виконується раніше)
a Задача 3: Укажіть на плакаті (плакат з метеликом виконується раніше)
![]()
![]()
![]()
![]()
![]()
![]() фигури, симетричні відносно прямої а.
фигури, симетричні відносно прямої а.
Задача 4: Розфарбуйте ліву частину метелика, нанесіть на праву частину
симетричний малюнок
Задача 5: Виміряйте довжини відрізків, симетричних відносно прямої а. Зробіть висновок.
Задача 6: Чи є у метелика ще вісь симетрії? Чи є у метелика вісь симетрії?
Задача 7: Знайдіть в слові МЕТЕЛИК літери,що мають вертикальну вісь симетрії, горизонтальну.
В якості виконання домашнього завдання запропонуйте учням знайти іншу схему виготовлення метелика, виготовити за цією схемою, нанести на готового метелика симетричний малюнок.


про публікацію авторської розробки
Додати розробку