"Довідник з геометрії для учнів 7 класу та вчителів математики"
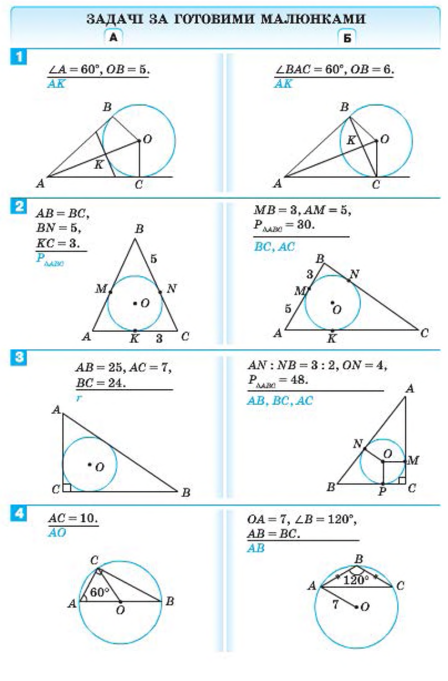
Підготувала
вчитель математики та інформатики
Поберезького навчально-виховного комплексу
Пушко Орися Володимирівна
ГЕОМЕТРИЧНІ ФІГУРИ. ТОЧКА, ПРЯМА, ПРОМІНЬ
ВІДРІЗОК. ВИМІРЮВАННЯ ВІДРІЗКІВ.
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ
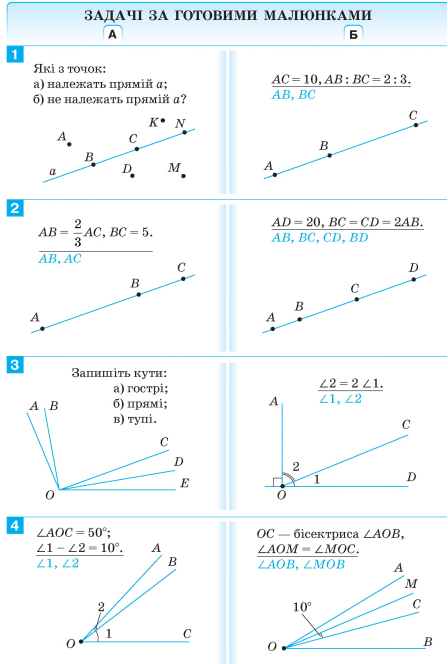
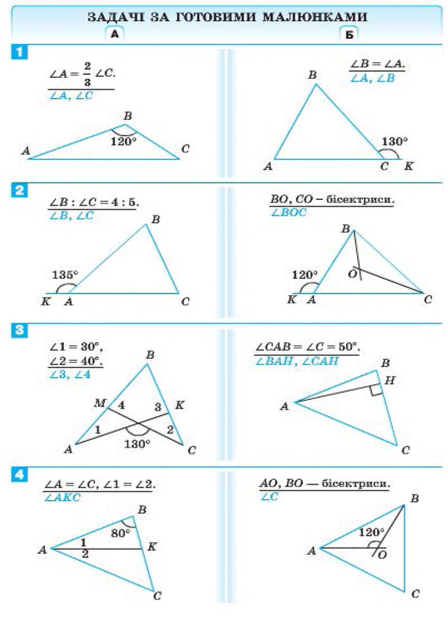
Відрізком називають частину прямої, яка складається з усіх точок цієї прямої, що лежать між двома її точками, разом із цими точками. Ці точки називають кінцями відрізка. Усі інші точки
цього відрізка – його внутрішні точки.
Два відрізки перетинаються, якщо вони мають тільки одну спільну внутрішню точку.
Кожний відрізок має певну довжину, більшу за нуль.
Два відрізки називають рівними, якщо рівні їх довжини.
Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його внутрішньою точкою.
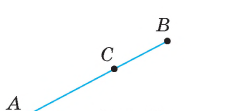АВ=АС+СВ
КУТ. ВИМІРЮВАННЯ КУТІВ.
БІСЕКТРИСА КУТА
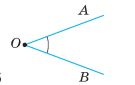
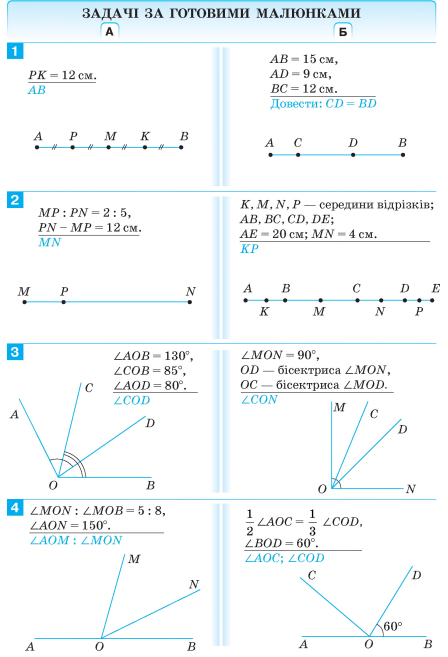
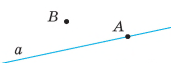
Кут — це геометрична фігура, яка складається з двох променів, що виходять з однієї точки.
Промені називають сторонами кута, а їх спільний початок — вершиною кута.
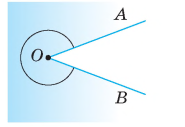
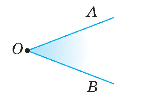
Будь-який кут ділить площину на дві частини. Якщо кут не є розгорнутим, то одну із частин називають внутрішньою областю кута, а іншу — зовнішньою (зафарбована).
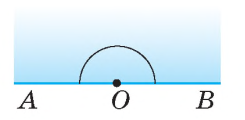
Розгорнутий кут — це кут, сторони якого є доповняльними променями.
Кожний кут має певну градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°.
Два кути називають рівними, якщо в них однакові градусні міри.
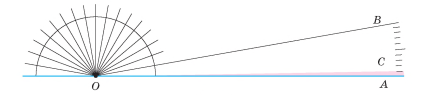
Основна властивість вимірювання кутів.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
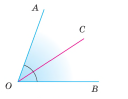Бісектрисою кута називають промінь, який виходить з його вершини і ділить кут навпіл.
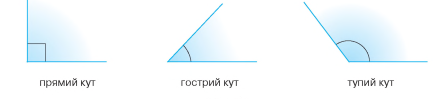
Кут називають прямим, якщо його градусна міра дорівнює 90°, гострим, якщо він менший від прямого, тупим, якщо він більший за прямий, але менший від розгорнутого.
СУМІЖНІ КУТИ
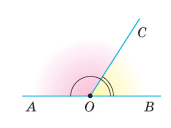Два кути називають суміжними, якщо одна сторона в них є спільною, а дві інші сторони цих кутів є доповняльними променями.
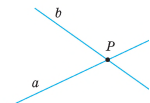
ВЕРТИКАЛЬНІ КУТИ. КУТ МІЖ ДВОМА ПРЯМИМИ, ЩО ПЕРЕТИНАЮТЬСЯ
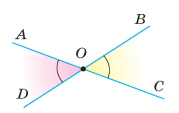
Два кути називають вертикальними, якщо сторони одного з них є доповняльними променями сторін другого.
Кутом між прямими, що перетинаються, називають менший з кутів, що утворилися при перетині цих прямих.
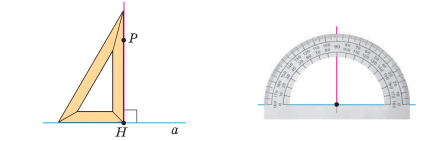
ПЕРПЕНДИКУЛЯРНІ ПРЯМІ. ПЕРПЕНДИКУЛЯР. ВІДСТАНЬ ВІД ТОЧКИ ДО ПРЯМОЇ
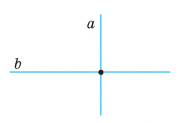
Дві прямі називають перпендикулярними, якщо вони перетинаються під прямим кутом.
Через будь-яку точку площини проходить лише одна пряма, перпендикулярна до даної прямої.
Відрізки або промені називають перпендикулярними, якщо вони лежать на перпендикулярних прямих.
Перпендикуляром до прямої, проведеним з даної точки, називають відрізок прямої, перпендикулярної до даної, один з кінців якого — дана точка, а другий — точка перетину прямих. Довжину цього відрізка називають відстанню від точки до прямої.
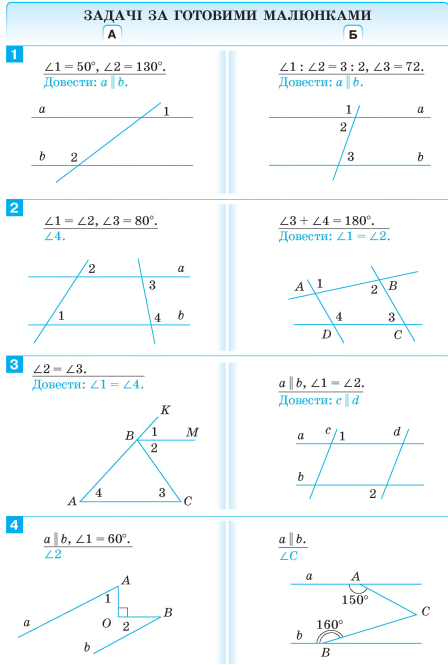
ПАРАЛЕЛЬНІ ПРЯМІ
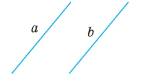Дві прямі на площині називають паралельними, якщо вони не перетинаються.
Аксіома паралельності прямих.
Через точку, що не лежить на даній прямій, проходить тільки одна пряма, паралельна даній.
Відрізки або промені називають паралельними, якщо вони лежать на паралельних прямих.
КУТИ, УТВОРЕНІ ПРИ ПЕРЕТИНІ ДВОХ ПРЯМИХ СІЧНОЮ. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ
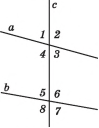
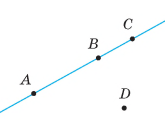
Пряма с називається січною для прямих а і в, якщо вона перетинає їх у двох точках.
При перетині прямих а і Ь січною с утворилося вісім кутів:
внутрішні односторонні кути: 4 і 5; 3 і 6;
внутрішні різносторонні кути: 4 і 6; 3 і 5;
відповідні кути: 1 і 5; 2 і 6; 3 і 7; 4 і 8.
ВЛАСТИВІСТЬ ПАРАЛЕЛЬНИХ ПРЯМИХ. ВЛАСТИВОСТІ КУТІВ, УТВОРЕНИХ ПРИ ПЕРЕТИНІ ПАРАЛЕЛЬНИХ ПРЯМИХ СІЧНОЮ
ТРИКУТНИК І ЙОГО ЕЛЕМЕНТИ
Трикутником називають фігуру, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які сполучають ці точки.
Точки називають вершинами трикутника, а відрізки — його сторонами.
Кожний трикутник має три вершини, три сторони і три кути, які ще називають елементами трикутника.
Суму довжин усіх сторін трикутника називають його периметром.
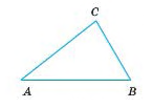Р = АС + СВ + АВ
Залежно від величини кутів розрізняють такі види трикутників: гострокутні, прямокутні, тупокутні.
РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР
Геометричні фігури називають рівними, якщо їх можна сумістити накладанням.
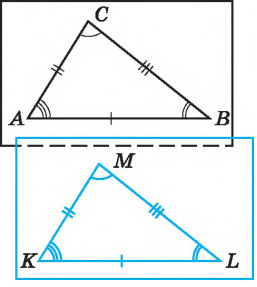Для позначення рівності трикутників використовують звичайний знак рівності:
АВС = КLМ.
У такій рівності має значення послідовність запису вершин трикутника.
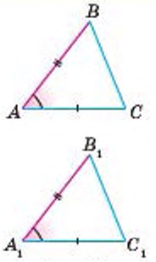
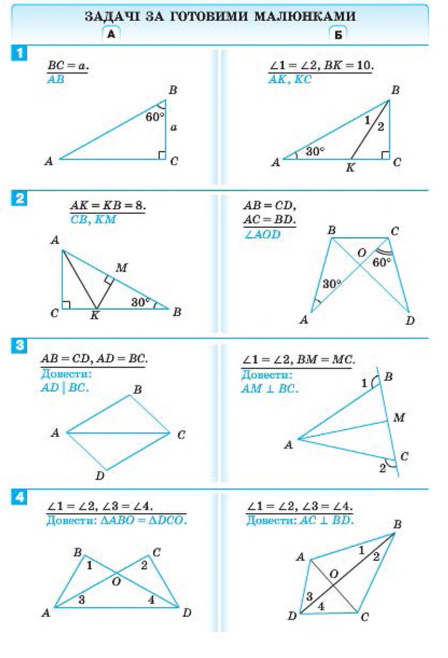
ПЕРША ТА ДРУГА ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ
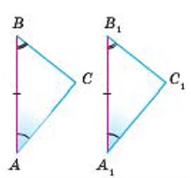
РІВНОБЕДРЕНИЙ ТРИКУТНИК
Трикутник називають рівнобедреним, якщо в нього дві сторони рівні.
Рівні сторони рівнобедреного трикутника називають бічними сторонами, а його третю сторону — основою.
Трикутник, усі сторони якого мають різні довжини, називають різностороннім.
Трикутник, усі сторони якого рівні, називають рівностороннім.
МЕДІАНА, БІСЕКТРИСА І ВИСОТА ТРИКУТНИКА. ВЛАСТИВІСТЬ БІСЕКТРИСИ РІВНОБЕДРЕНОГО ТРИКУТНИКА
Медіаною трикутника називають відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
Бісектрисою трикутника називають відрізок бісектриси кута трикутника, що сполучає вершину трикутника з точкою протилежної сторони.
Висотою трикутника називають перпендикуляр, проведений з вершини трикутника до прямої, що містить його протилежну сторону.
ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ
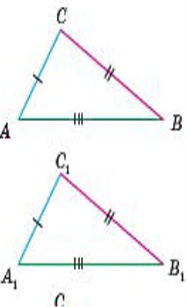
СУМА КУТІВ ТРИКУТНИКА
ЗОВНІШНІЙ КУТ ТРИКУТНИКА ТА ЙОГО ВЛАСТИВОСТІ. СПІВВІДНОШЕННЯ МІЖ СТОРОНАМИ І КУТАМИ ТРИКУТНИКА
Зовнішнім кутом трикутника називають кут, суміжний з кутом цього трикутника.
ПРЯМОКУТНІ ТРИКУТНИКИ. ВЛАСТИВОСТІ ТА ОЗНАКИ РІВНОСТІ ПРЯМОКУТНИХ ТРИКУТНИКІВ
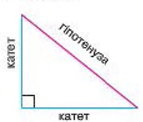
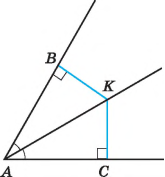
Трикутник називають прямокутним, якщо один з його кутів прямий.
Сторону прямокутного трикутника, яка лежить проти прямого кута, називають гіпотенузою, а дві інші сторони — катетами.
Властивості прямокутних трикутників
1. Сума гострих кутів прямокутного трикутника дорівнює 90°.
2. Гіпотенуза прямокутного трикутника більша за будь- який з його катетів.
3. Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.
4. Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, що лежить проти цього катета, дорівнює 30°.
5.У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи.
Ознаки рівності прямокутних трикутників
- Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні.
- Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету і прилеглому до нього куту іншого, то такі трикутники рівні.
- Якщо гіпотенуза і гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому куту іншого, то такі трикутники рівні.
- Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету і протилежному йому куту іншого, то такі трикутники рівні.
НЕРІВНІСТЬ ТРИКУТНИКА
Кожна сторона трикутника менша від суми двох інших сторін, але більша за модуль їх різниці.
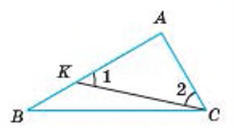
| АВ - АС | < ВС < АВ + АС
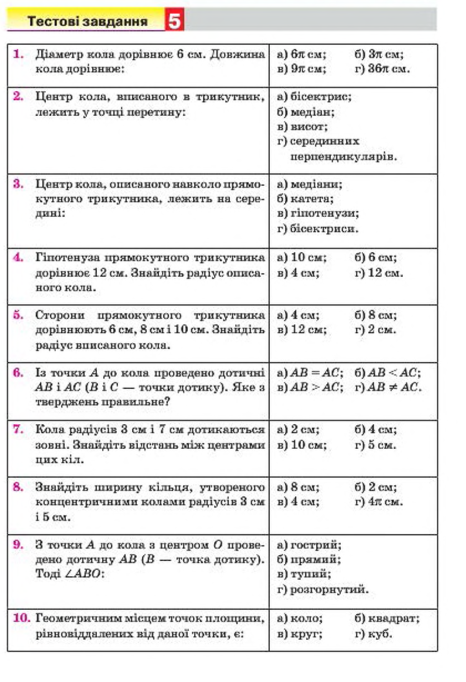
КОЛО. КРУГ
Колом називають геометричну фігуру, яка складається з усіх точок площини, рівновіддалених від даної точки.
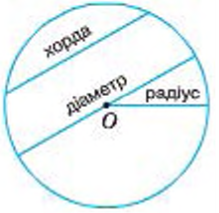Цю точку називають центром кола. Відрізок, що сполучає центр з будь-якою точкою кола, називають радіусом.
Відрізок, що сполучає дві точки кола, називають хордою. Хорду, що проходить через центр кола, називають діаметром.
Коло разом з його внутрішньою областю називають кругом.
Центром, радіусом, діаметром, хордою круга називають відповідно центр, радіус, діаметр, хорду кола, яке є межею даного круга.
ДОТИЧНА ДО КОЛА, ЇЇ ВЛАСТИВОСТІ
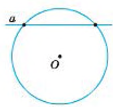
Пряму, яка має дві спільні точки з колом, називають січною.
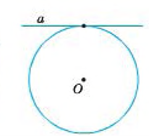Відстань від центра кола до січної менша від радіуса.
Дотичною до кола називають пряму, яка має з колом лише одну спільну точку. Цю точку називають точкою дотику.
КОЛО, ВПИСАНЕ В ТРИКУТНИК
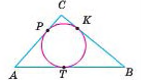
Коло називають вписаним у трикутник, якщо воно дотикається до всіх сторін цього трикутника.
КОЛО, ОПИСАНЕ НАВКОЛО ТРИКУТНИКА
Серединним перпендикуляром до відрізка називають пряму, що проходить через середину відрізка перпендикулярно до нього.
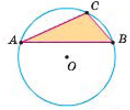Коло називають описаним навколо трикутника, якщо воно проходить через усі вершини цього трикутника.
Трикутник називають вписаним у коло.
ВЗАЄМНЕ РОЗМІЩЕННЯ ДВОХ КІЛ
І. Два кола можуть не перетинатися, тобто не мати спільних точок
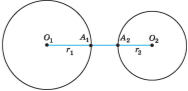
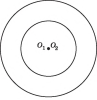
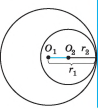
Два кола називають концентричними, якщо вони мають спільний центр.
II. Два кола можуть мати одну спільну точку.
У такому разі кажуть, що кола дотикаються, а спільну точку називають точкою дотику кіл.
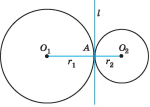
Дотик двох кіл називають зовнішнім, якщо центри кіл лежать по різні боки від точки дотику.
Дотик двох кіл називають внутрішнім, якщо центри кіл лежать по один бік від точки дотику.
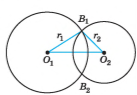III. Два кола можуть мати дві спільні точки, тобто кола перетинаються.
ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК
Геометричним місцем точок площини називають фігуру, що складається з усіх точок площини, які мають певну властивість.
1. Геометричне місце точок, рівновіддалених від даної точки на дану відстань, — коло, радіус якого дорівнює даній відстані.
2. Геометричне місце точок, відстань від яких до даної точки не перевищує даної відстані, — круг, радіус якого дорівнює даній відстані.
3. Геометричне місце точок, які рівновіддалені від сторін кута та належать його внутрішній області, — бісектриса даного кута
- Геометричне місце точок, які рівновіддалені від кінців відрізка, — серединний перпендикуляр до даного відрізка.
5. Геометричне місце точок, які рівновіддалені від даної прямої на задану відстань, — дві прямі, паралельні даній прямій, кожна точка яких знаходиться на заданій відстані від прямої.
ЗМІСТ
ГЕОМЕТРИЧНІ ФІГУРИ. ТОЧКА, ПРЯМА, ПРОМІНЬ
ВІДРІЗОК. ВИМІРЮВАННЯ ВІДРІЗКІВ.
ВЕРТИКАЛЬНІ КУТИ. КУТ МІЖ ДВОМА ПРЯМИМИ, ЩО ПЕРЕТИНАЮТЬСЯ
ПЕРПЕНДИКУЛЯРНІ ПРЯМІ. ПЕРПЕНДИКУЛЯР. ВІДСТАНЬ ВІД ТОЧКИ ДО ПРЯМОЇ
КУТИ, УТВОРЕНІ ПРИ ПЕРЕТИНІ ДВОХ ПРЯМИХ СІЧНОЮ. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ
ВЛАСТИВІСТЬ ПАРАЛЕЛЬНИХ ПРЯМИХ. ВЛАСТИВОСТІ КУТІВ, УТВОРЕНИХ ПРИ ПЕРЕТИНІ ПАРАЛЕЛЬНИХ ПРЯМИХ СІЧНОЮ
ПЕРША ТА ДРУГА ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ
МЕДІАНА, БІСЕКТРИСА І ВИСОТА ТРИКУТНИКА. ВЛАСТИВІСТЬ БІСЕКТРИСИ РІВНОБЕДРЕНОГО ТРИКУТНИКА
ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ
ЗОВНІШНІЙ КУТ ТРИКУТНИКА ТА ЙОГО ВЛАСТИВОСТІ. СПІВВІДНОШЕННЯ МІЖ СТОРОНАМИ І КУТАМИ ТРИКУТНИКА
ПРЯМОКУТНІ ТРИКУТНИКИ. ВЛАСТИВОСТІ ТА ОЗНАКИ РІВНОСТІ ПРЯМОКУТНИХ ТРИКУТНИКІВ
ДОТИЧНА ДО КОЛА, ЇЇ ВЛАСТИВОСТІ
КОЛО, ОПИСАНЕ НАВКОЛО ТРИКУТНИКА
Аксіома – це теорема, яка довела своє алібі.
(Б. Дабузький)
Алгебра і геометрія — єдині країни, де панують тиша й мир.
(М. Аньєзі)
1
про публікацію авторської розробки
Додати розробку