Розробка уроку на тему: "Властивості кутів трикутника. Розв'язування задач", 7 клас
|
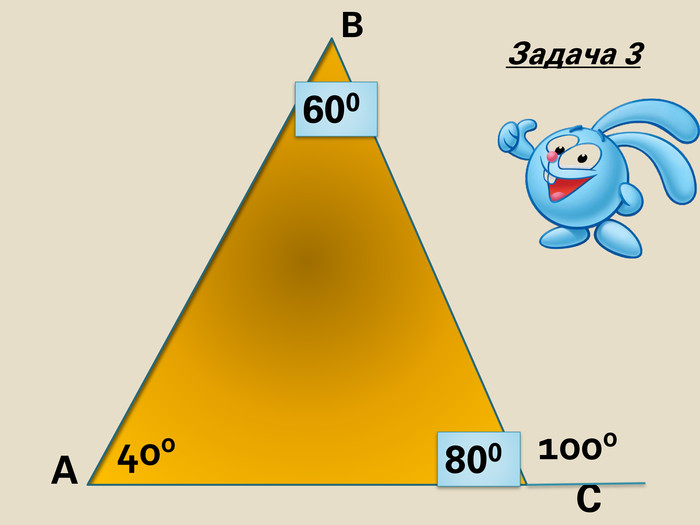
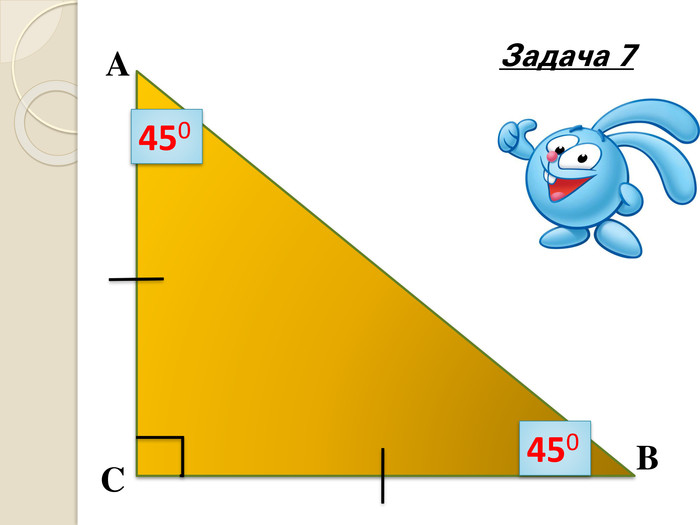
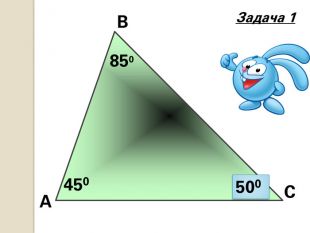
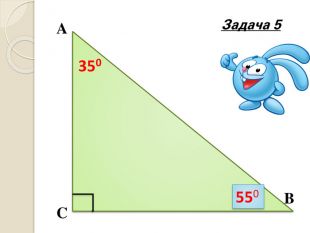
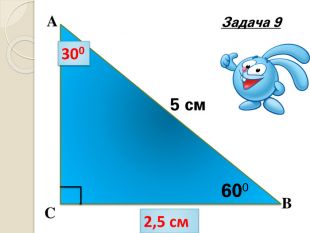
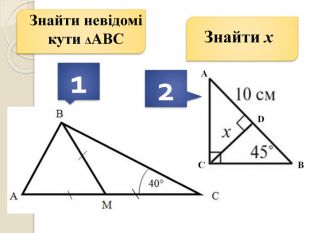
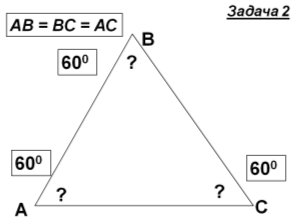
Знайти кути трикутника АВС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
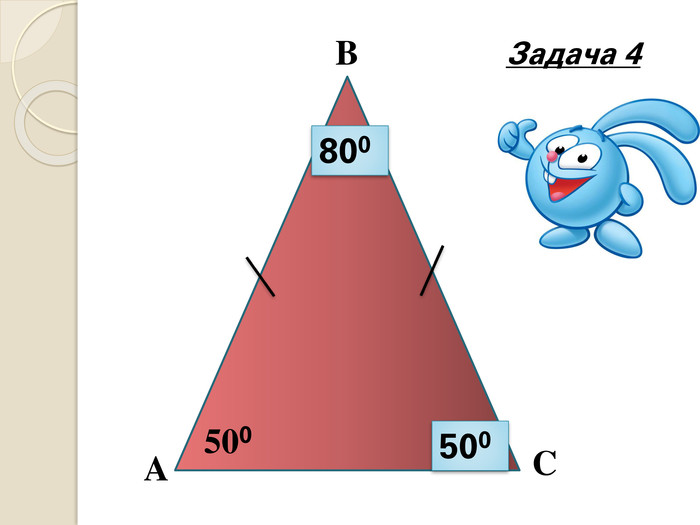
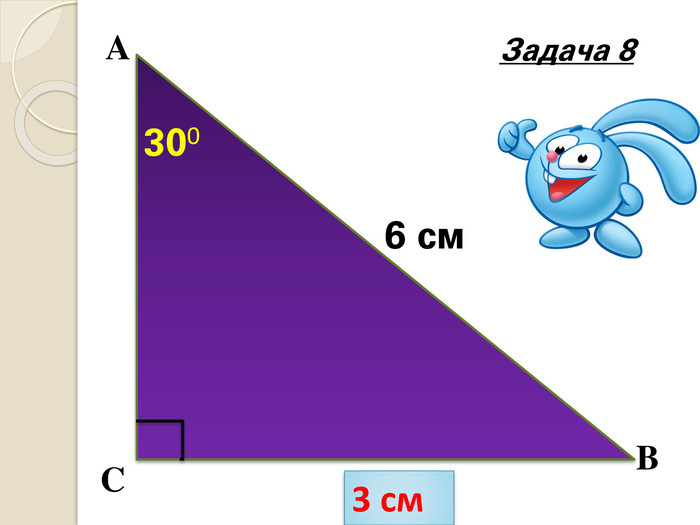
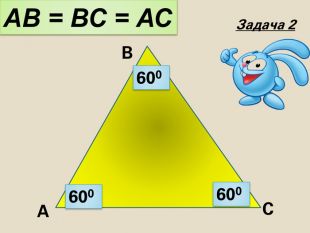
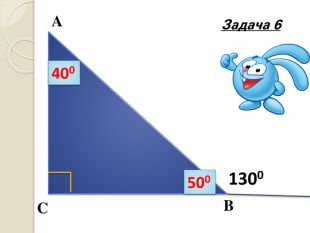
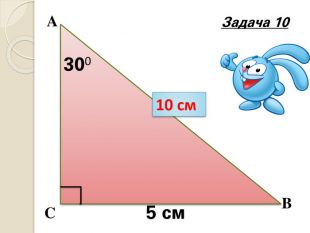
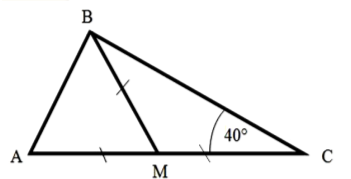
Знайти кути трикутника АВС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
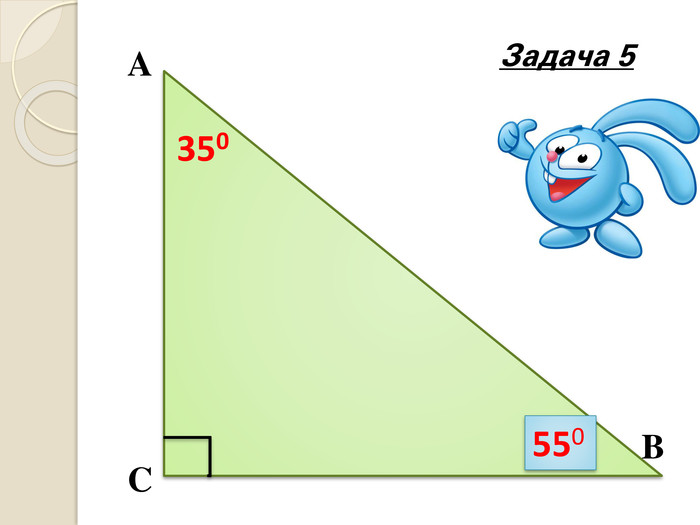
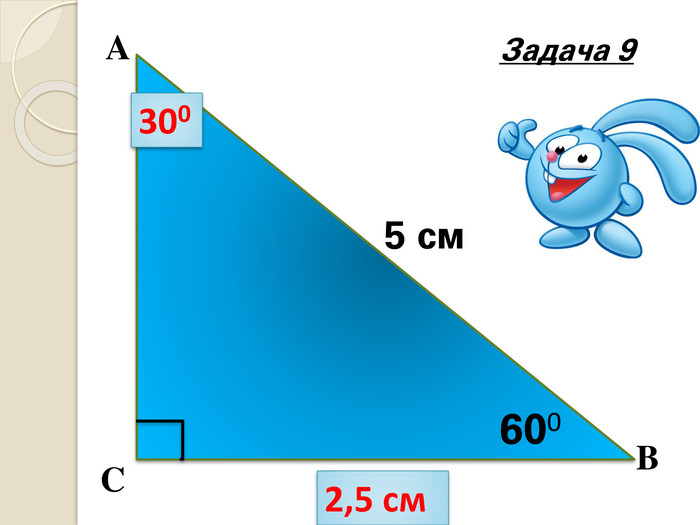
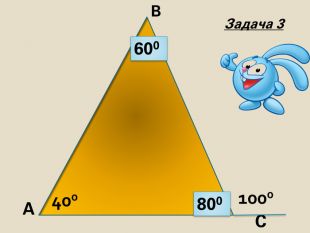
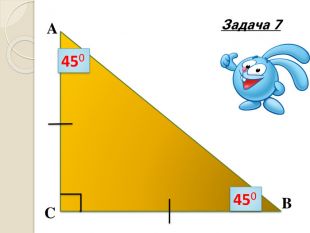
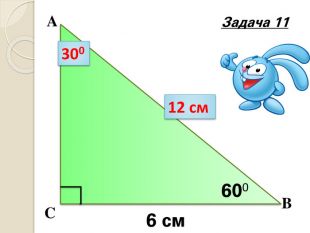
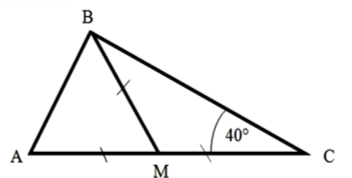
Знайти кути трикутника АВС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
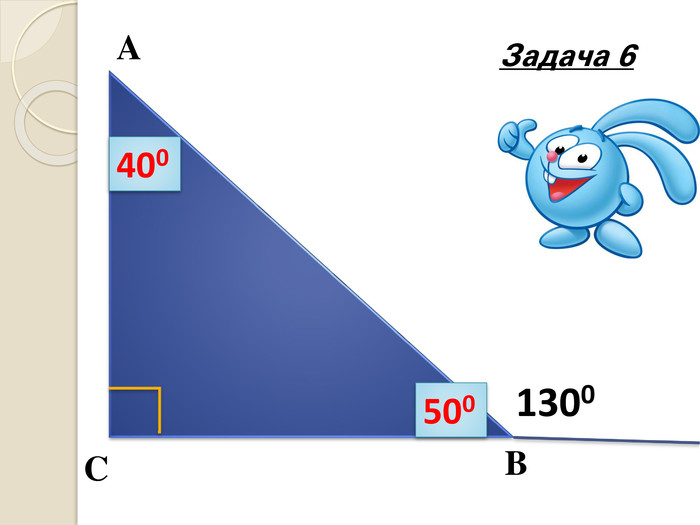
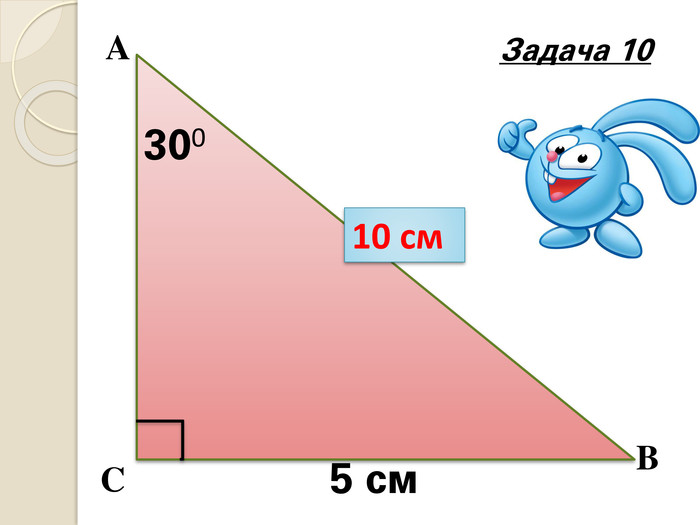
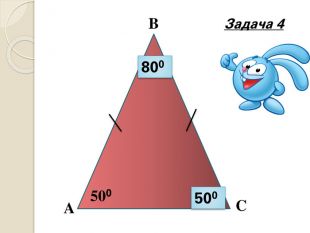
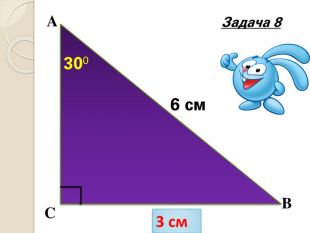
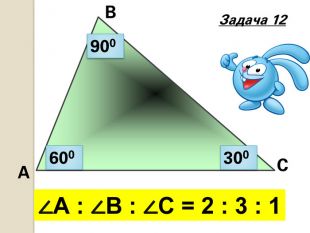
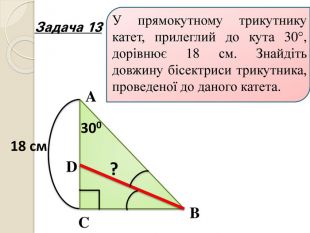
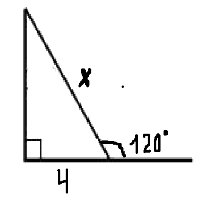
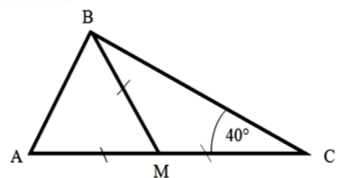
Знайти x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
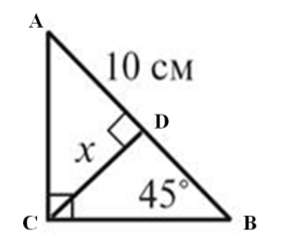
|
Знайти x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
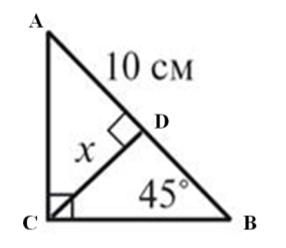
|
Знайти x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Клас: 7
Тема. Властивості кутів трикутника. Розв’язування задач.
Мета: закріпити та узагальнити знання учнів про властивості кутів трикутника; розвивати вміння учнів застосовувати знання з теми до розв’язування задач; розвивати творче та логічне мислення; підвищувати інтерес до геометрії; виховувати самостійність та відповідальність, культуру спілкування.
Тип уроку: застосування знань, умінь та навичок.
Наочність і обладнання: мультимедійний проектор, презентація, картки-плакати з задачами, картки з задачами для роботи в парі та для самостійної роботи, картки з висловом.
Якщо ви хочете навчитися плавати, то сміливо ступайте у воду, а якщо хочете навчитися розв'язувати задачі, то розв'язуйте їх!
Дж. Пойа
(На дошці до початку уроку заготовлено частини вислову, які закріплено магнітом, а також на зворотній частині дошки закріплено магнітом малюнки до задач.)
ХІД УРОКУ
I. Організаційний момент
Повідомлення теми і мети уроку. Мотивація навчальної діяльності. Обговорення епіграфу (слайд 1, 2).
II. Перевірка домашнього завдання
Перевірка правильності виконання за готовими записами (слайди 3-5).
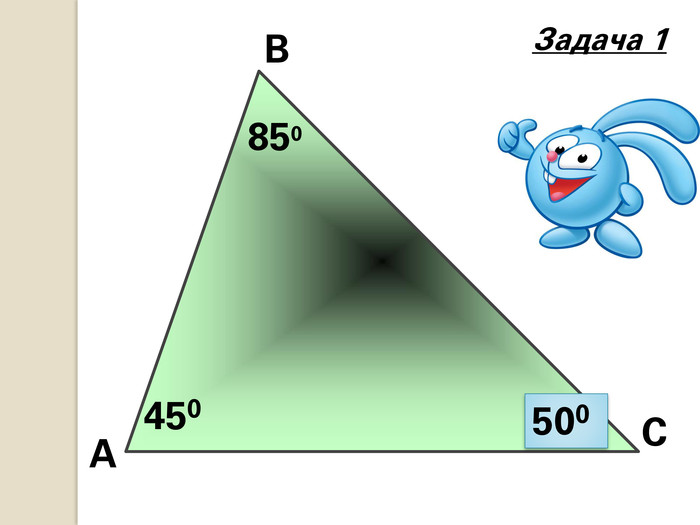
№ 488
За теоремою про суму кутів трикутника:
∠А + ∠В + ∠С = 1800.
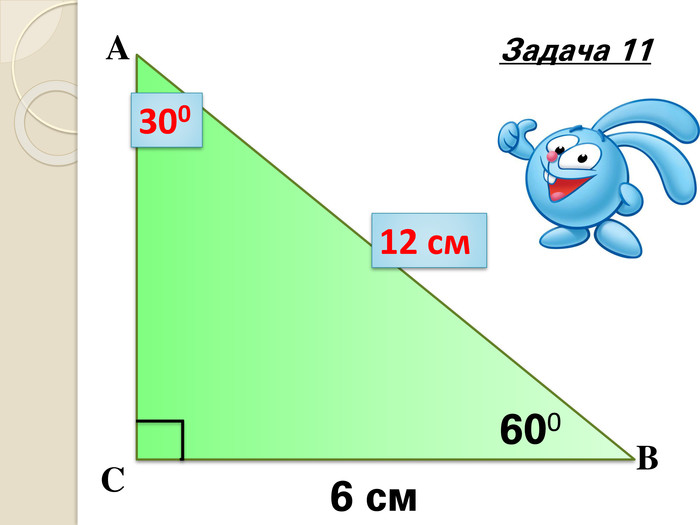
600 + 450 + 400 + х =1800
х = 350
Відповідь: 350
№ 505
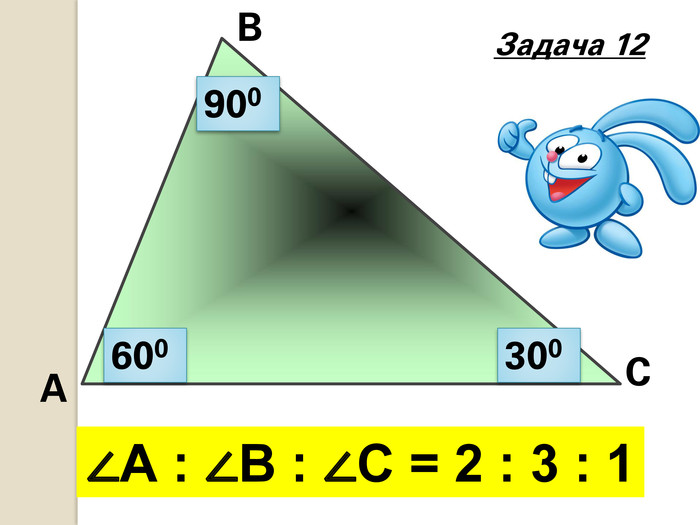
Нехай k – коефіцієнт пропорційності, тоді гострі кути прямокутного трикутника - 3k, 7k.
Оскільки сума гострих кутів прямокутного трикутника дорівнює 900, то маємо рівняння:
3k + 7k = 900
10k = 900
k = 90
3k = 3 • 90 = 270
7k = 7 • 90 = 630
 Відповідь: 270, 630.
Відповідь: 270, 630.
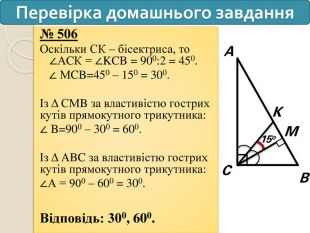
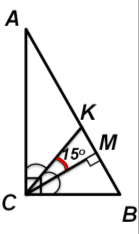
№ 506
Оскільки СК – бісектриса, то ∠АCК = ∠KCB = 900:2 = 450.
∠ МCB=450 – 150 = 300.
Із Δ CМB за властивістю гострих кутів прямокутного трикутника:
∠ B=900 – 300 = 600.
Із Δ АBC за властивістю гострих кутів прямокутного трикутника:
∠А = 900 – 600 = 300.
Відповідь: 300, 600.
ІІІ. Актуалізація опорних знань
Бліц-опитування за запитаннями (слайди 6-14):
- Що таке трикутник?
- Назвіть основні елементи трикутника.
- Що таке периметр трикутника?
- Які є види трикутників (залежно від величин кутів)?
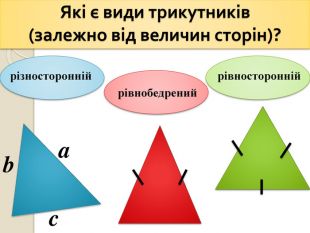
- Які є види трикутників (залежно від величин сторін)?
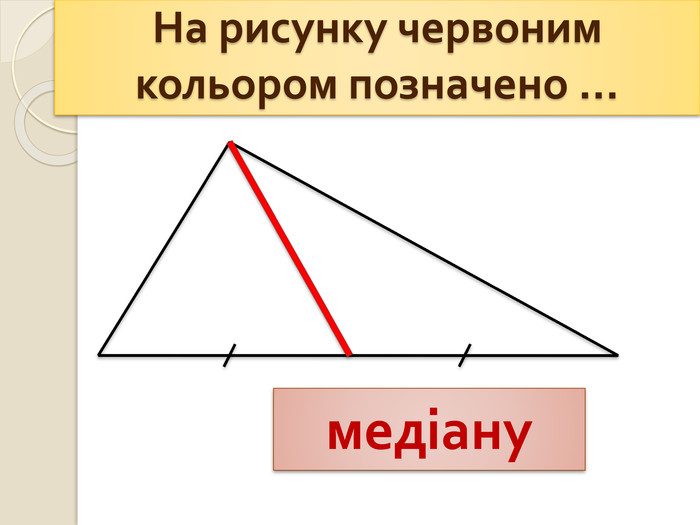
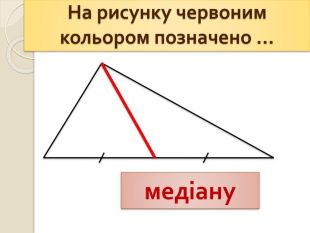
- На рисунку червоним кольором позначено … медіану.
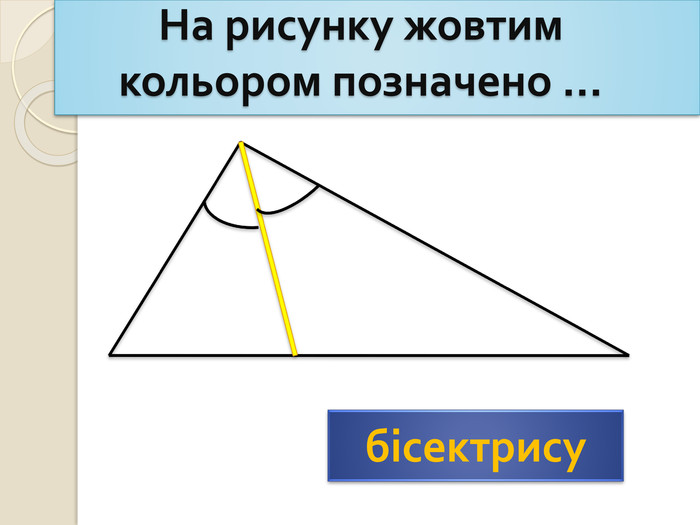
- На рисунку жовтим кольором позначено … бісектрису.
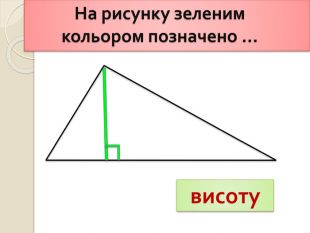
- На рисунку зеленим кольором позначено … висоту.
- Чому дорівнює сума кутів у різносторонньому трикутнику?
- Чому дорівнює сума кутів у рівнобедреному трикутнику?
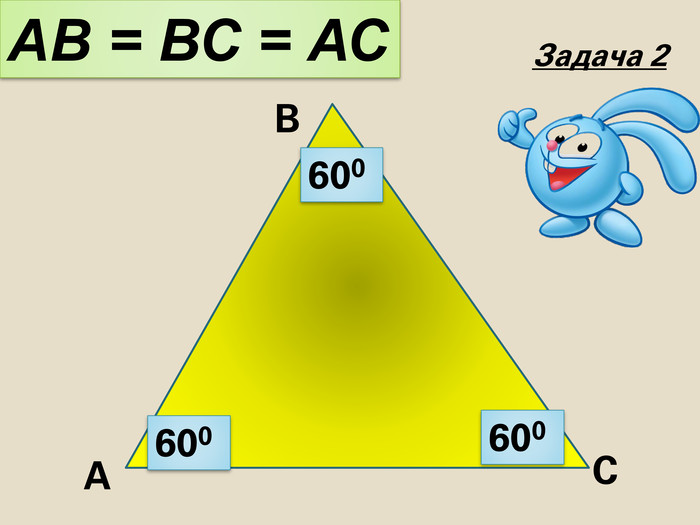
- Чому дорівнює сума кутів у рівносторонньому трикутнику?
Учитель: Як можна узагальнити ці три відповіді?
- Чи може трикутник мати два прямих кути?
- Чи може трикутник мати два тупих кути?
- Чи може трикутник мати прямий і тупий кути?
IV. Застосування знань і умінь до розв’язування задач.
- Розв'язування задач усно за готовими малюнками, колективно та з коментарем. (слайди 15-28)
Розв’язавши задачі, ви зможете прочитати вислів видатного ученого. За кожну правильно розв’язану задачу відкривається частина вислову: «Математику вже навіть задля того треба вивчати, що вона розум до ладу приводить» М.В.Ломоносов.
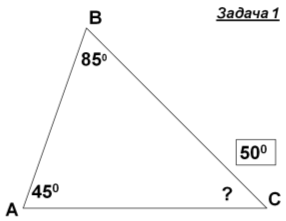
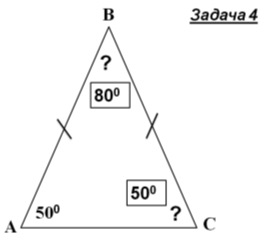
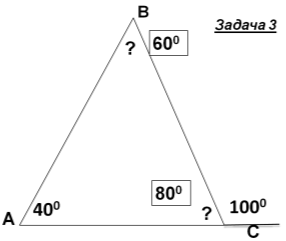
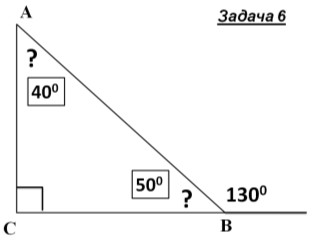
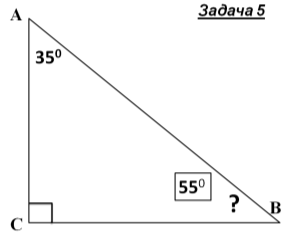
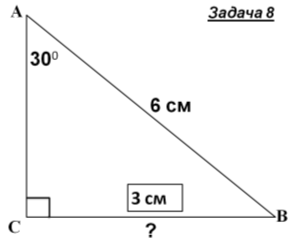
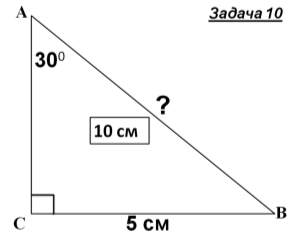
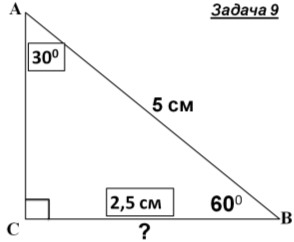
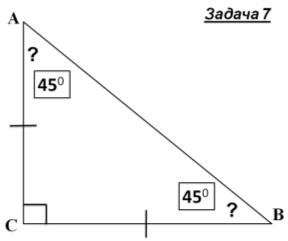
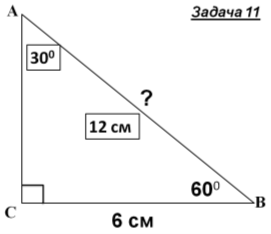
- Розв'язування задач із записами розв’язку у зошитах і на дошці.
 (слайди 29, 30)
(слайди 29, 30)
- Розв'язування задач за готовими малюнками у парах.
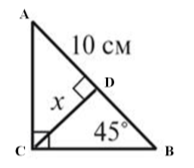 Учням роздаються картки з малюнками до задач. Після розв’язування задач у парі, рішення обговорюється з класом за готовими малюнками на дошці. (слайди 31-33)
Учням роздаються картки з малюнками до задач. Після розв’язування задач у парі, рішення обговорюється з класом за готовими малюнками на дошці. (слайди 31-33)
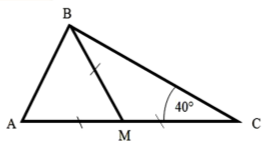
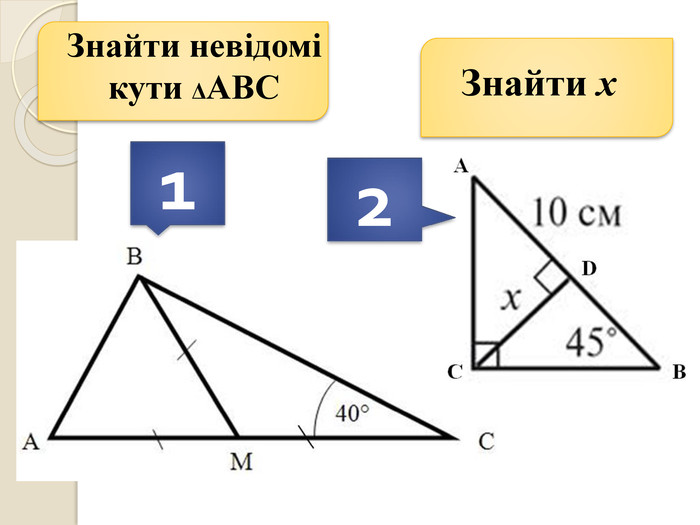
Знайти кути трикутника АВС Знайти x
- Складання плану розв’язання задачі.
«Мозковий штурм» (слайди 35-37)
Учні виконують малюнок у зошиті, записують скорочену умову та разом з вчителем (робить записи на дошці) складають план розв’язання.
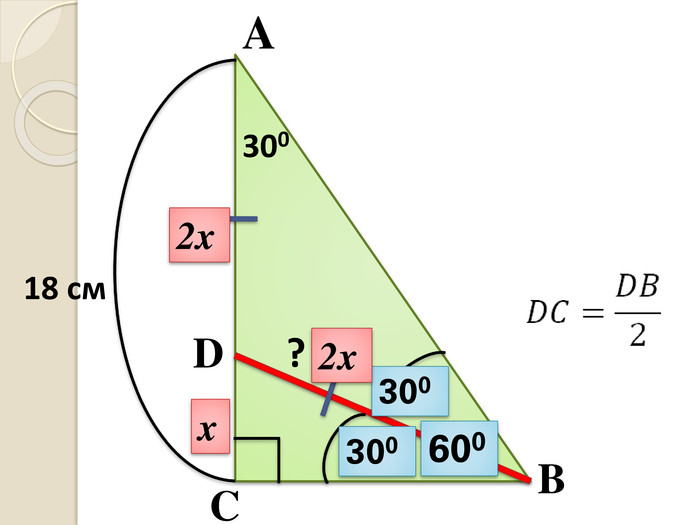
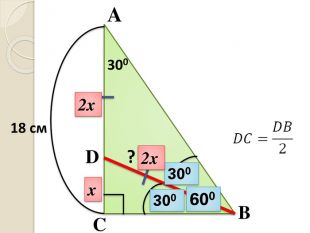
Задача 13 У прямокутному трикутнику катет, прилеглий до кута 30°, дорівнює 18 см. Знайдіть довжину бісектриси трикутника, проведеної до даного катета.
-
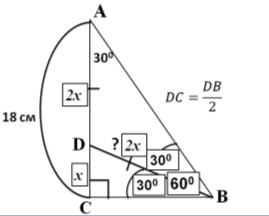 ∠АBC = 60o;
∠АBC = 60o;
- ∠АBD = ∠DBC = 30o;
- ΔADB – рівнобедрений, AD = DB;
- ΔDCB, ∠C = 90o: DC = DB/2;
- Нехай DC = x, DB = AD = 2x;
- x + 2x = 18;
- BD = 2x.
V. Домашнє завдання (слайд 38)
- Оформити задачу 13.
- Повторити розділ ІІІ.
- Розв’язати задачі № 498, 507.
VІ. Самостійна робота (слайд 39)
Учням роздаються індивідуальні картки (два варіанти) з задачами.
Додаток 1
VІІ. Підсумок уроку (слайди 40-42)
Вправа «Незакінчене речення»
- Сума кутів трикутника дорівнює ….
- Сума гострих кутів прямокутного трикутника дорівнює …
- Прямокутний трикутник може мати лише…
- Тупокутний трикутник може мати лише…
За наявності часу розглянути задачу:
Чи існує прямокутний трикутник, зображений на рисунку? Чому?
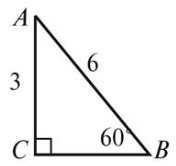
Вчитель підводить підсумок уроку та оцінює учнів.
Рефлексія
Учні продовжують речення:
На уроці я...
• дізнався...
• зрозумів...
• навчився...
• на наступному уроці я хочу...
Варіант 1
|
|
1.Знайти х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
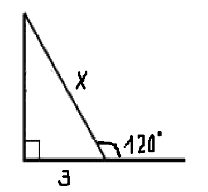
2.Один із зовнішніх кутів трикутника дорівнює 1200. Знайдіть внутрішні кути, не суміжні з ним, якщо один з них на 200 менший за другий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Додаток 1
Варіант 2
|
|
1.Знайти х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Один із зовнішніх кутів трикутника дорівнює 1200. Знайдіть внутрішні кути, не суміжні з ним, якщо один з них у 3 рази менший за другий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


про публікацію авторської розробки
Додати розробку